0 引言
透明平行板模型是研究缝内支撑剂运移规律的主要装置。针对常规砂岩储集层的研究[10⇓-12]和支撑剂运移的微观分析[13-14]多采用光滑直缝设备。为适应复杂裂缝支撑剂运移研究的需要，相继研发了单一分支缝设备[15]、多分支缝设备[16]、多级分支缝设备[17]、主缝缝宽变化设备[18]、主缝缝高变化设备[19]等，对流体黏度和密度，支撑剂密度、粒径和浓度，排量，分支缝角度，缝宽和缝高变化及分支缝的分流等因素进行了研究[20-21]，基本明确了这些因素对主缝和分支缝中支撑剂运移的影响。但对于多数量、多类型分支缝条件下支撑剂的运移规律研究较少。另外，小粒径支撑剂有更强的运移能力，具有易进入微裂缝[22]扩大有效支撑的缝网体积和高闭合压力下导流能力衰减速度慢[23]的优势，在现场应用中常搭配大粒径支撑剂组合注入以改善近井裂缝的支撑情况，但不同粒径支撑剂的注入顺序对复杂裂缝内支撑剂运移的影响尚待明确。此外，Chun等[24]研究表明倾斜裂缝中支撑剂的运移能力更强，蒋廷学等[25]研究发现支撑剂在粗糙裂缝内的运移沉降与光滑裂缝相比有较大差异，大尺寸裂缝模拟装置能够更真实地反映支撑剂的运移情况[8]。
本文采用考虑裂缝粗糙度和多数量、多类型分支缝的设备开展支撑剂运移模拟实验，进一步明确复杂裂缝支撑剂运移规律，指导体积压裂方案优化设计。
1 实验介绍
1.1 实验装置
大型可视化复杂裂缝颗粒运移模拟装置（见图1 ）的主缝长5 m，高0.6 m，宽5 mm，主缝两侧设置有10条分支缝，一侧有30°、45°、90°等3条垂直分支缝，1条水平分支缝及1条60°倾斜分支缝，另一侧有150°、135°、90°等3条垂直分支缝，1条水平分支缝及1条60°倾斜分支缝，文中简称为30°、45°、90°、135°、150°、水平及60°倾斜分支缝。分支缝长1 m，高0.6 m，宽3 mm。主缝与分支缝的组合方式、相对位置如图1 所示，其中30°和150°分支缝距入口1 m，45°和135°分支缝距入口2 m，90°分支缝距入口3 m，水平分支缝在距入口3~4 m处，60°倾斜分支缝在距入口4~5 m处。通过控制各分支缝出口的阀门来开启或关闭分支缝，形成不同形态的复杂裂缝。
利用相似原理进行室内装置与实际裂缝参数的转换以保证实验的科学性。黏性力是缝内支撑剂运移的主要动力，需保证实验和实际缝内流动的雷诺数相等。雷诺数的计算公式为：
$Re=\frac{\rho vL}{\mu }$
雷诺数是通过圆管流动推导的，圆管流场的特征长度为其直径（D）。定义圆管的过流断面面积为A，润湿周长为P，则有：
$D=\frac{4\left( {\text{ }\!\!\pi\!\!\text{ }{{D}^{2}}}/{4}\; \right)}{\text{ }\!\!\pi\!\!\text{ }D}=\frac{4A}{P}$
对于非圆管（流体充满）流动，定义水力直径为过流断面面积与周长之比的4倍，作为流场的特征长度。对于高为H、宽为w的裂缝，其水力直径为：
${{d}_{\text{f}}}=\frac{4A}{P}=\frac{4wH}{2\left( w+H \right)}=\frac{4w}{2\left( \frac{w}{H}+1 \right)}$
实际裂缝的缝高远大于缝宽，w/H为可忽略的小量，则有df=2w，代入（1）式可得：
$R{{e}_{\text{f}}}=\frac{2\rho vw}{\mu }$
由实际和实验缝内流动的雷诺数相等可得：
$\frac{{{\rho }_{\text{n}}}{{v}_{\text{n}}}{{w}_{\text{n}}}}{{{\mu }_{\text{n}}}}=\frac{{{\rho }_{\text{m}}}{{v}_{\text{m}}}{{w}_{\text{m}}}}{{{\mu }_{\text{m}}}}$
实验缝宽与实际缝宽相等，均为5 mm，实验所用压裂液的密度、黏度和支撑剂的粒径、密度均与实际相同。因此（5）式可简化为vn=vm，即保证实验和实际裂缝缝内流体流速相等，便可实现流动相似。实际施工排量为双翼裂缝总排量，实验模拟的是单翼裂缝，所以实验排量和实际排量的关系如下：
$\frac{{{Q}_{\text{n}}}}{2{{A}_{\text{n}}}}=\frac{{{Q}_{\text{m}}}}{{{A}_{\text{m}}}}$
1.2 实验材料与实验方案
实验支撑剂使用830/380 μm（20/40目）、380/212 μm（40/70目）和212/109 μm（70/140目）石英砂，压裂液采用黏度为5 mPa·s的滑溜水，恒定砂比加砂，其他实验参数如表1 所示。实验排量为16.2 m3/h，根据（6）式计算缝内流体流速为1.5 m/s，相当于现场层厚10 m储集层9 m3/min的排量。
表1 不同实验的参数设置 |
| 序号 | 排量/(m3·h-1) | 砂比/% | 粒径 | 分支缝角度 | 分支缝开启时机 |
|---|---|---|---|---|---|
| 1 | 16.2 | 10 | 380/212 μm（40/70目） | 30°、150°、45°、135°、90° | 常开 |
| 2 | 16.2 | 10 | 380/212 μm（40/70目） | 90°、水平、60°倾斜 | 常开 |
| 3 | 16.2 | 10 | 380/212 μm（40/70目） | 30°、150°、45°、135°、90°、水平、60°倾斜 | 常开 |
| 4 | 16.2 | 10 | 212/109 μm（70/140目） | 30°、150°、45°、135°、90°、水平、60°倾斜 | 常开 |
| 5 | 16.2 | 8 | 380/212 μm（40/70目） | 30°、150°、45°、135°、90° | 常开 |
| 6 | 16.2 | 12 | 380/212 μm（40/70目） | 30°、150°、45°、135°、90° | 常开 |
| 7 | 16.2 | 10 | 380/212 μm（40/70目） | 30°、150°、45°、135°、90° | 先关后开 |
| 8 | 16.2 | 10 | 380/212 μm（40/70目） | 30°、150°、45°、135°、90° | 先开后关 |
| 9 | 16.2 | 10 | 先小后大 | 30°、150°、45°、135°、90° | 常开 |
| 10 | 16.2 | 10 | 先大后小 | 30°、150°、45°、135°、90° | 常开 |
实验前，在配液罐中配制黏度为5 mPa·s的滑溜水，并准备一定量的支撑剂，控制分支缝出口的阀门开启实验所需的分支缝。根据实验的排量16.2 m3/h可得液体注入速度为4.5 L/s，乘以砂比可得每秒的加砂量（加砂速度），支撑剂的注入时间为支撑剂体积除以加砂速度。
按照实验排量和加砂速度进行实验，实验过程中每1 s采集1次主缝及各分支缝的排量数据，每5 s采集1次砂堤形态图片。当支撑剂注入完成后，继续注入不含支撑剂的压裂液60 s，保证实验过程图片的完整采集。
选取支撑剂注入过程中主缝砂堤高度稳定时（平衡阶段）的砂堤形态进行分析，由于实验注入的支撑剂量大于裂缝的体积，所以砂堤均能达到平衡状态。通过MATLAB的图像识别功能，提取砂堤的轮廓数据，可绘制砂堤三维图像，以直观展示砂堤形态及复杂裂缝的位置关系。根据砂堤的轮廓数据还可绘制砂堤形态对比曲线。
定义了裂缝充填比例和近井未充填程度这两个评价参数。裂缝充填比例为裂缝中被砂堤占据的裂缝体积占总裂缝体积的比例。近井未充填程度为主缝砂堤的平均高度所在水平线、井筒（主缝左边界）和砂堤形态轮廓所围成的区域的面积。
实验方案如下。①不同复杂裂缝形态下支撑剂运移规律实验。使用380/212 μm（40/70目）石英砂分别开启近井分支缝、远井分支缝、全部分支缝进行3组实验，即实验1—3，再使用212/109 μm（70/140目）石英砂开启全部分支缝进行1组实验，即实验4。支撑剂量为40 L，支撑剂注入时间为90 s。②不同砂比下支撑剂运移规律实验。开展砂比分别为8%，10%，12%的恒定砂比加砂实验，即实验5、实验1、实验6。支撑剂量分别为32，40，49 L，支撑剂注入时间为90 s。③不同分支缝开启时机下支撑剂运移规律实验。开展分支缝常开（分支缝持续扩展进液）、先关后开（前期主缝进液后期分支缝开启进液）、先开后关（前期分支缝进液后期分支缝停止扩展不进液）3种情况下的支撑剂运移实验，即实验1、实验7、实验8。支撑剂量为40 L，支撑剂注入时间为90 s。其中实验7和8分别在支撑剂注入45 s后开启和关闭分支缝。④不同加砂顺序下支撑剂运移规律实验。为明确不同粒径支撑剂组合注入时加砂顺序对复杂裂缝内支撑剂运移铺置的影响，进行了830/380 μm（20/40目）、380/212 μm（40/70目）和212/109 μm（70/140目）石英砂这3种支撑剂先小后大和先大后小两种加砂顺序的实验，即实验9和实验10。支撑剂量为40 L，支撑剂注入时间为90 s，3种支撑剂的体积比为1∶1∶1。
2 实验结果及讨论
2.1 不同复杂裂缝形态下支撑剂运移规律
2.1.1 开启近井分支缝和远井分支缝的对比
2.1.1.1 主缝砂堤形态及形成过程
如图3 所示，实验1中距井筒最近的分支缝（30°、150°）在距主缝入口1 m处，实验2中距井筒最近的分支缝（90°）在距主缝入口3 m处。为了更加清晰地展示砂堤轮廓，将裂缝中未被支撑剂充填的部分调整为蓝色。因为分支缝的分流会使分支后主缝流量减小，所以实验1和实验2的主缝砂堤分别在1 m和3 m之后明显升高（见图4 ）。实验1中携砂液经过近井分支缝分流后主缝支撑剂铺置长度小于实验2（见图4 ）。
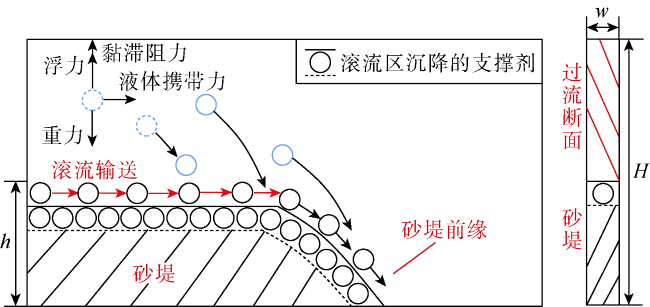
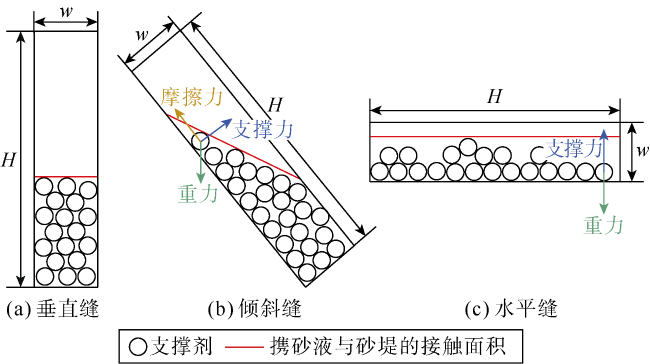
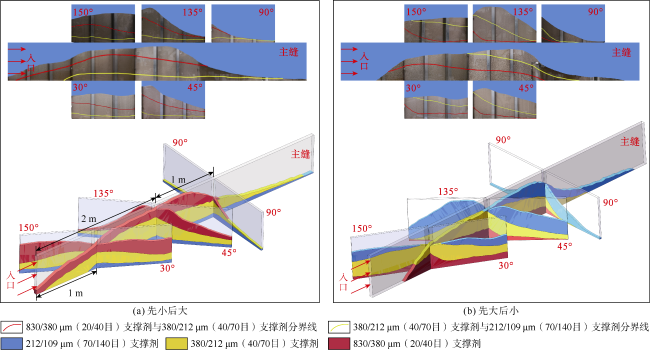
对分支后主缝砂堤的增高过程进行分析可以更好地理解支撑剂在复杂裂缝中的运移机理。如图5 所示，假设携砂液在缝内流动为层流，不考虑支撑剂与裂缝壁面及支撑剂之间的相互作用时，支撑剂在水平方向上受压裂液的液体携带力作用（水平运移速度约为液体流速的0.7~0.9倍[31]），在垂直方向上受重力、浮力和黏滞阻力作用。水平和垂直方向上的力共同作用使支撑剂产生如图5 所示的倾斜运移轨迹，这决定了支撑剂必然会不断沉降。早期研究根据裂缝纵向支撑剂的浓度差异从裂缝底部到上部划分出砂堤、滚流区、悬浮区和无砂区[10,32]。图6a 和图6b 分别为实验2主缝1~2 m位置处砂堤达到平衡时和平衡后注入不含支撑剂的压裂液时的支撑剂分布状态。如图6a 所示，滑溜水能提供的黏滞阻力很小，支撑剂进入裂缝后会迅速沉降并静止在裂缝底部形成砂堤；砂堤上方高度很小的区域为滚流区，由于滚流区的支撑剂浓度高且流速快，所以表现为颜色与砂堤相似的模糊条带；滚流区上方为悬浮区，悬浮区支撑剂浓度低，所以能够看到裂缝的壁面。不同区域会不断发生支撑剂的交换。实验过程可分为3个阶段：①初期砂堤升高阶段，支撑剂进入裂缝后快速沉降在裂缝底部，砂堤高度、长度同时增加；②砂堤平衡阶段，砂堤高度达到稳定，砂堤长度持续增加；③砂堤冲蚀阶段，向裂缝中注入无支撑剂的压裂液，近井砂堤被冲蚀，砂堤前缘向裂缝深部推移。3个阶段均有支撑剂被不断输送到砂堤前缘：在初期砂堤升高阶段和砂堤平衡阶段观测到了滚流区（见图6a ），而注入不含支撑剂的压裂液时（见图6b ），裂缝中没有复杂的颗粒悬浮沉降，只有砂堤和上方压裂液的流动，依然观测到了滚流区，近井砂堤被侵蚀，砂堤前缘向前推移。因此，滚流区产生的条件是裂缝中存在砂堤、砂堤上方有流体的流动，滚流区的作用是将支撑剂输送到砂堤前缘。
在砂堤平衡阶段，滚流区不断将近井支撑剂向砂堤前缘输送，但砂堤高度依然保持相对稳定，说明近井砂堤存在支撑剂补充，而来源只有悬浮区的支撑剂沉降。所以砂堤平衡过程是支撑剂沉降和滚流输送之间的平衡。在初期砂堤升高阶段，砂堤高度不断增加，则说明了此时支撑剂的沉降量大于滚流区的输送量，而随着砂堤高度增加，沉降速率和滚流输送速率不断变化达到动态平衡，进入砂堤平衡阶段。
前文明确了砂堤上方有流体流动就会产生滚流区，流体流动所产生的液体携带力作用则是滚流区产生的主要原因。根据液体携带力产生的原理，流体速度越大液体携带力越强，所以滚流区中支撑剂的输送速率和数量（滚流输送的效率）与压裂液的流速呈正相关。压裂液流速与砂堤上方裂缝的过流断面面积相关：
${{v}_{\text{f}}}=\frac{Q}{S}=\frac{Q}{w\left( H-h \right)}$
随着砂堤的升高，压裂液流速和滚流输送效率相应提高。根据前文的层流假设，若支撑剂垂直方向受力不变，其在裂缝中的沉降速率不变。但随着砂堤上方压裂液流速的升高，流体流动可能会向湍流转变，虽然湍流中颗粒运动理论尚未明确，但相关实验表明湍流所形成的复杂流场会延缓支撑剂的沉降并有利于运移[31]，另外裂缝的粗糙度也会进一步增加流场的复杂程度，所以流场复杂的情况下支撑剂的沉降速率下降，滚流输送速率提高，砂堤高度较小时便可达到平衡。在裂缝入口处，携砂液经射孔（5个射孔）进入裂缝时，会在近井裂缝中产生复杂的流场，越接近入口流场越复杂。由于复杂流场的影响，图4 所示的4组实验中主缝0~100 cm范围内的砂堤随着流场的逐渐稳定而逐渐升高。而实验1和实验2在经过分支缝的分流之后，主缝中携砂液的流速减小，滚流输送效率下降，沉降速率增加，动态平衡被打破，需要更高的砂堤高度以达到重新平衡。所以分支后主裂缝砂堤会明显升高，分支缝分流量越多，主缝砂堤高度增加幅度越大。
2.1.1.2 分支缝砂堤形态及形成过程
对实验1和实验2的分支缝砂堤形态进行分析，图7 为实验1和实验2中90°分支缝内的砂堤形态，图8 为流量变化曲线。实验1中90°分支缝距离井筒最远，流量最小，砂堤形态近似为三角形，充填比例为32%。实验2中90°分支缝距离井筒最近，流量较实验1的90°分支缝有明显提升，砂堤形态近似为矩形，充填比例为59%。因此，距井筒越近，分支缝流量越大，进入的支撑剂越多，裂缝的充填比例越大。
垂直裂缝中砂堤前缘大多为逐渐降低的斜坡状（见图3 ）。实验2前期水平分支缝砂堤前缘为不规则的指状（见图9 ），后期水平分支缝整个裂缝被支撑剂充填（见图3b ），60°倾斜分支缝砂堤前缘也不规则，砂堤高度和充填比例均大于垂直分支缝。由于水平分支缝距入口较远，所以需要较长时间支撑剂才能进入，但很快支撑剂就充满整个水平分支缝，所以这里所说的实验2前期为支撑剂注入70 s时。
支撑剂在不同倾斜程度裂缝中的受力不同使砂堤表现出不同的形态。如图10a 所示，在垂直缝中，壁面对支撑剂施加水平方向的支撑力，支撑剂的沉降主要受垂直方向由重力主导的合力影响，所以垂直裂缝中壁面对支撑剂运移的影响不大，除非裂缝宽度小于支撑剂粒径的2倍。如图10b 所示，在倾斜缝中，支撑剂受垂直于裂缝壁面的支撑力，这使支撑剂在沿裂缝壁面沉降时受到平行于壁面的摩擦力而减缓沉降，壁面粗糙时会增大摩擦力。另外，倾斜裂缝中携砂液与砂堤的作用面积（图10 中红线指示）较垂直裂缝有所增加，被液体携带而发生滚流的支撑剂数量随之增加。支撑剂沉降的减缓和滚流区面积的增大使支撑剂在裂缝纵向的分布范围增加，形成近似矩形形态。如图10c 所示，在水平缝中，裂缝壁面的支撑力完全平衡了支撑剂的重力，携砂液与砂堤的接触面为整个裂缝面，支撑剂层上方存在携砂液流动的通道，理论上整个水平裂缝都是滚流区，裂缝高度方向完全充满支撑剂。而由于壁面粗糙度的非均匀性，支撑剂在滚流过程中受到的摩擦阻力不同，所以出现了图9 所示的指状前缘。因此，在缝内流量相同的情况下，随着裂缝倾斜程度增加，滚流区范围增加，支撑剂沉降减缓，支撑剂更易在裂缝中运移，裂缝支撑面积增大。但需要注意的是，水平缝的支撑剂无法在缝宽方向完全充填，支撑缝宽要小于裂缝缝宽。
缝内支撑剂的最终分布受裂缝扩展及支撑剂运移的综合影响，在埋藏较深、上覆地层压力较大的储集层中，水平缝的扩展相对困难[33]，裂缝进液量很少甚至为零。而进入裂缝的支撑剂数量与流量呈正比，所以此时水平缝中支撑剂充填情况较差。
2.1.2 开启近井分支缝和全部分支缝的对比
实验1与实验3分别开启了近井分支缝和全部分支缝。开启全部分支缝后，携砂液依旧首先进入近井分支缝，所以实验1和实验3近井分支缝的砂堤形态相差不大，主缝砂堤形态相差也较小（见图4 ）。实验3中远井水平分支缝中有少量支撑剂进入，60°倾斜分支缝流量很小则无支撑剂进入。所以在天然裂缝发育的地层，应增大排量和砂量，改善远井分支缝的充填。
2.1.3 开启全部分支缝条件下注入不同粒径支撑剂的对比
实验4开启了全部分支缝，采用粒径更小的212/109 μm（70/140目）石英砂，对比图3c 和图3d 可以发现，212/109 μm（70/140目）石英砂改善了远井水平分支缝和60°倾斜分支缝的充填，但对近井主缝和分支缝的充填不如380/212 μm（40/70目）石英砂。
2.2 不同砂比下支撑剂运移规律
随着砂比的增加，裂缝中单位时间内沉降的支撑剂量增加，需要更高的砂堤高度才能达到平衡，所以主缝0~150 cm的砂堤高度有较明显的提升（见图11a ），近井未充填程度降低（见图11b ）[29]，砂比增加有助于改善近井裂缝的充填。裂缝中部（150~250 cm）砂堤形态变化不大，砂堤最大高度从48.06 cm增加到50.44 cm，砂堤高度已经非常接近裂缝高度，所以增幅较小。砂比从8%增加到10%时，砂堤前缘（250~400 cm）向前推移，但砂比从10%增加到12%时砂堤前缘变化不大。由于近井砂堤的充填改善和砂堤前缘的推进，随着砂比的增加，裂缝充填比例增加（见图11b ）。
进入分支缝的支撑剂数量与分支缝的流量成正比。根据图3a 的裂缝形态和图8 的分支缝流量曲线分析可知，30°和150°分支缝距离井筒最近，缝内流量最大；45°和135°分支缝与井筒的相对距离较远，缝内流量较小；90°分支缝距离井筒最远，缝内流量最小。流量差异导致进入分支缝的支撑剂数量不同，所以30°、150°分支缝砂堤形态为矩形铺置（见图12a 、12b ）；45°、135°分支缝中砂堤仅能在分支缝0~20 cm和0~30 cm处达到最大高度，呈现梯形铺置（见图12c 、12d ）；90°分支缝中支撑剂只能依靠重力向裂缝中滑落，砂堤呈现三角形铺置（见图12e ）。
如图12f 所示，随着砂比的增加，30°和150°分支缝中裂缝充填比例增幅不大且基本线性增加。而砂比从8%增加到10%时，其他分支缝的充填比例增幅较大，所以对于缝内流量较小、支撑剂进入比较困难的远井分支缝，提升砂比增加携砂液中支撑剂的含量可提高进入分支缝中支撑剂的数量，改善分支缝的支撑。砂比从10%增加到12%时，远井分支缝充填比例增幅减小，因为此时分支缝中砂堤的最大高度已经接近裂缝高度。当砂比增加到一定程度时，继续增加砂比砂堤高度提高幅度较小但施工风险增加，所以最优砂比应在曲线拐点附近。
2.3 不同分支缝开启时机下支撑剂运移规律
分支缝先开后关实验中，分支缝前期开启时，支撑剂随携砂液进入分支缝，砂堤高度快速增长。当分支缝关闭后，支撑剂无法通过携带作用进入分支缝，主缝100 cm处砂堤被冲蚀而降低，该位置处的30°和150°分支缝中砂堤高度大于主缝砂堤高度，支撑剂也不能通过重力进入分支缝，所以30°和150°分支缝砂堤停止增长。分支缝关闭后主缝200 cm处砂堤高度变化不大，该位置处的45°和135°分支缝中砂堤也停止增长。但主缝300 cm处的砂堤高度增加明显，支撑剂还可以通过重力进入该位置处的90°分支缝中，分支缝关闭后90°分支缝中砂堤继续增加，所以分支缝充填比例略大于先关后开时。实际压裂主要以主裂缝扩展为主，大部分分支缝不会一直扩展，而是由于缝内支撑剂的持续堆积出现前期扩展后期停止扩展，或者前期不扩展后期压力升高扩展的情况，所以分支缝先关后开和分支缝先开后关的实验更加接近实际分支缝的扩展过程，而这两种条件下分支缝充填情况都不如分支缝常开时。因此，在优化压裂加砂参数时应有针对性地改善分支缝的充填。
2.4 不同加砂顺序下支撑剂运移规律
支撑剂粒径越大其重力越大，在垂直方向上的受力增加，沉降速率提高，滚流输送难度增加，更易沉降在近井，需要更高的携砂液流速才能达到平衡，所形成的砂堤越高。所以支撑剂先小后大注入时（见图15a ），砂堤呈现大粒径支撑剂在小粒径支撑剂上部层叠铺置状态；支撑剂先大后小注入时（见图15b ），主缝、30°和150°分支缝中砂堤呈现小粒径支撑剂在大粒径支撑剂砂堤前缘处铺置状态，45°、135°和90°分支缝中砂堤呈现小粒径支撑剂在大粒径支撑剂上部层叠铺置状态。
如图17 所示，先大后小注入时，由于830/380 μm（20/40目）支撑剂的注入量较少，未达到其平衡高度，所以后续注入的380/212 μm（40/70目）支撑剂继续在830/380 μm（20/40目）砂堤上方沉降，并达到平衡。继续注入212/109 μm（70/140目）支撑剂时近井砂堤已经超过其平衡高度，所以212/109 μm（70/140目）支撑剂在主缝0~194 cm处基本不沉降，而由于裂缝中一直有携砂液流动，此范围内砂堤会因为不断的滚流输送而被侵蚀，被侵蚀的主要为380/212 μm（40/70目）支撑剂，在近井处有部分830/380 μm（20/40目）支撑剂被侵蚀。由于380/212 μm（40/70目）支撑剂平衡高度小于830/380 μm（20/40目）支撑剂，并且其达到平衡之后又被侵蚀，所以先大后小注入时的砂堤高度低于先小后大注入时且砂堤起始位置距井筒较远（见图16 ）。由于在主缝194 cm之后380/212 μm（40/70目）支撑剂砂堤高度逐渐降低，并且经过45°和135°分支缝的分流作用，212/109 μm（70/140目）支撑剂和近井被侵蚀的380/212 μm（40/70目）与830/380 μm（20/40目）支撑剂会大量沉降在此范围内，最终砂堤高度在271~329 cm处高于先小后大注入时（见图16 ）。由于212/109 μm（70/140目）支撑剂大量沉降在该范围内，运移距离缩短，所以砂堤最终的铺置长度小于先小后大时（见图16 ）。
30°分支缝位于距入口1 m处，此处先小后大注入时主缝砂堤高于先大后小时和380/212 μm（40/70目）单独注入时（见图16 ），由于主缝砂堤的影响，所以30°分支缝中先小后大注入时砂堤高于其他两种注入方式（见图18a ）。90°分支缝位于主裂缝距入口3 m处，此处主缝先小后大注入时砂堤低于其他两种注入方式（见图16 ），所以90°分支缝0~60 cm处先小后大注入时砂堤低于先大后小注入，0~67 cm处先小后大注入时砂堤低于380/212 μm（40/70目）单独注入时（见图18b ）；先大后小注入时830/380 μm（20/40目）和380/212 μm（40/70目）支撑剂在90°分支缝中铺置长度有限，后期注入的支撑剂铺置高度高但是运移距离短，所以先大后小注入时90°分支缝60~100 cm处砂堤低于先小后大注入时；380/212 μm（40/70目）单独注入时砂堤铺置长度最短。
先大后小注入时主缝0~194 cm处的砂堤会被侵蚀而降低，所以位于主缝1 m处的30°分支缝中注入212/109 μm（70/140目）支撑剂时会侵蚀0~10 cm处380/212 μm（40/70目）支撑剂的砂堤（见图19a ）。由于380/212 μm（40/70目）支撑剂在分支缝10~100 cm处高度较低，所以侵蚀仅发生在分支缝入口处。主缝2m附近的砂堤高度变化不大，所以此处45°分支缝入口处的砂堤并未明显侵蚀，图19b中的蓝色曲线和红色曲线不存在交叉。
分支缝中砂堤的铺置面积取决于进入分支缝的流量，由于实验分支缝长度有限，所以可以通过分支缝的流量大小及变化来判断进入的支撑剂数量。如图20 所示，不同支撑剂注入顺序时30°和150°分支缝的流量均最大，45°和135°分支缝次之，90°分支缝最小。距离入口越远的分支缝分配的流量越小，所以近井分支缝的充填情况要好于远井分支缝。如图20a 所示，先小后大注入时，近井30°和150°分支缝的流量逐渐增加，而远井分支缝的流量在0~50 s时逐渐减小，这与图8 中单一粒径注入时的流量变化趋势相同，在50~60 s时，由于大量830/380 μm（20/40目）支撑剂沉降在30°和150°分支缝中，导致其流量减小，远井分支缝流量有所增加。如图20b 所示，先大后小注入时，近井30°和150°分支缝的流量逐渐减小，远井分支缝的流量有所增加，这将导致进入近井分支缝中的支撑剂减少，进入远井分支缝的支撑剂增多。近井分支缝流量减小的主要原因是前期注入的830/380 μm（20/40目）支撑剂在近井沉降高度达到27 cm，使近井分支缝入口的流动面积大幅减小。
实验通过缝内流速相等实现实验和实际裂缝的相似，但由于实验裂缝长度的限制，须减小砂量才能在有限的范围内获得整个砂堤形态，这使实验时间和施工时间之间有较大差距，对支撑剂先大后小注入时的结果带来影响。由于实验注入的830/380 μm（20/40目）支撑剂量较少，所以830/380 μm（20/40目）支撑剂未达到平衡便注入了380/212 μm（40/70目）支撑剂，而在实际施工中，注入时间显著增加后，830/380 μm（20/40目）支撑剂会达到平衡高度，之后再注入的380/212 μm（40/70目）支撑剂不会沉降在830/380 μm（20/40目）支撑剂砂堤的上方，而是沉降在砂堤的前缘（212/109 μm（70/140目）支撑剂便沉降在了380/212 μm（40/70目）支撑剂前缘），最终砂堤的形态应如图21 所示。而注入时间增加后，砂堤被侵蚀的时间和侵蚀量会大幅增加，近井裂缝的未充填区域会比实验显示的大得多。所以支撑剂先大后小注入后期要针对近井未充填区域进行相应的改善，比如尾追大粒径支撑剂或降低排量。此外，由于实际裂缝中830/380 μm（20/40目）支撑剂能够达到平衡高度，砂堤高度要比实验中高，其对分支缝流量的影响也更大，所以先大后小注入时830/380 μm（20/40目）支撑剂铺置范围内的分支缝充填情况不如先小后大注入时，而380/212 μm（40/70目）和212/109 μm（70/140目）支撑剂铺置范围内的分支缝充填情况会有改善。当不同粒径支撑剂组合注入时，830/380 μm（20/40目）支撑剂占比较小时可选择先大后小注入，对近井和裂缝中部分支缝的充填影响较小。
2.5 讨论
本文研究发现，体积压裂裂缝充填的主要问题是由于分支缝的分流作用，携砂液流量逐级减小，支撑剂运移能力逐步减弱，在主缝铺置长度减小，远井分支缝的流量很小，支撑效果较差。此外，分支缝前期或后期扩展进液的充填情况都不如持续扩展时，而实际分支缝不会一直扩展进液，因此实际分支缝的充填情况比实验显示的要差。以提高分支缝充填为主要目标，提出以下建议。
①推荐采用不同粒径支撑剂组合注入方式。本文研究表明212/109 μm（70/140目）支撑剂可增大主缝铺置长度并改善远井分支缝充填，但砂堤高度整体下降，近井主缝充填情况变差。不同粒径支撑剂组合注入可提高裂缝支撑效果，本文研究明确了加入212/109 μm（70/140目）支撑剂后砂堤在主缝和分支缝的铺置长度均大于380/212 μm（40/70目）单独注入时。因此，优先采用先小后大注入，在830/380 μm（20/40目）支撑剂用量较少时可采用先大后小注入并尾追大粒径支撑剂改善近井充填。
②提升排量。本文研究表明分支缝的进液量增加会明显改善分支缝的充填，因此对于天然裂缝发育的储集层，可提升排量以改善分支缝充填。
③提高砂比。分支缝进液量是限制支撑剂进入的主要因素，本文研究明确了提高砂比能够提高液体中的砂浓度从而改善分支缝的充填。砂比增加到一定值后，砂堤高度增幅减小，应通过实验确定最优砂比。
3 结论
砂堤平衡是颗粒沉降与滚流输送之间的动态平衡，砂比、支撑剂粒径、缝内流场和流量改变会导致颗粒沉降或滚流输送效率发生变化，砂堤会降低或升高以达到新的动态平衡。
分支缝的分流使分支后主缝砂堤高度提高，铺置长度减小，远井分支缝充填不理想。倾斜裂缝壁面会对支撑剂产生减缓沉降的摩擦力，支撑剂的铺置高度更高，支撑缝高较大，但支撑缝宽小于裂缝缝宽。壁面粗糙度的非均匀性使水平分支缝砂堤前缘呈指状。
砂比增加后近井主缝和远井分支缝的充填情况改善、主缝砂堤长度增加。但由于缝高的限制，砂比增加到一定值后随着砂比增加砂堤高度增幅逐渐减小。
分支缝先关后开时，分支缝开启后主缝中部砂堤升高。分支缝先开后关时，分支缝关闭后主缝砂堤被冲蚀，铺置长度增加。分支缝常开时分支缝的支撑效果最好，先关后开时支撑情况优于先开后关时。
支撑剂先小后大注入时，呈现小粒径在下大粒径在上的层叠铺置状态。支撑剂先大后小注入时，呈现小粒径支撑剂在大粒径支撑剂砂堤前缘处铺置状态，近井砂堤被大量侵蚀，首先注入的大粒径支撑剂在近井主缝形成较高的砂堤，会影响近井分支缝进液进而影响其充填。
符号注释：
A——过流断面面积，m2；An，Am——实际和实验裂缝入口面积，m2；D——圆管直径，m；df——裂缝内流动的水力直径，m；h——砂堤高度，m；H——缝高，m；L——流场的特征长度，m；P——润湿周长，m；Q——单翼缝内压裂液排量，m3/s；Qn，Qm——实际和实验施工排量，m3/min；Re——雷诺数；Ref——裂缝内流动的雷诺数；S——砂堤上方过流断面面积，m2；v——流场的特征速度，m/s；vf——压裂液流速，m/s；vn，vm——实际和实验的携砂液缝内初始流速，m/s；w——缝宽，m；wn，wm——实际和实验的裂缝宽度，m；μ——流体的动力黏度，Pa·s；μn，μm——实际和实验的携砂液黏度，Pa·s；ρ——流体密度，kg/m3；ρn，ρm——实际和实验的携砂液密度，kg/m3。