0 引言
1 基于DFN-FEM的缝口暂堵压裂复杂裂缝扩展理论
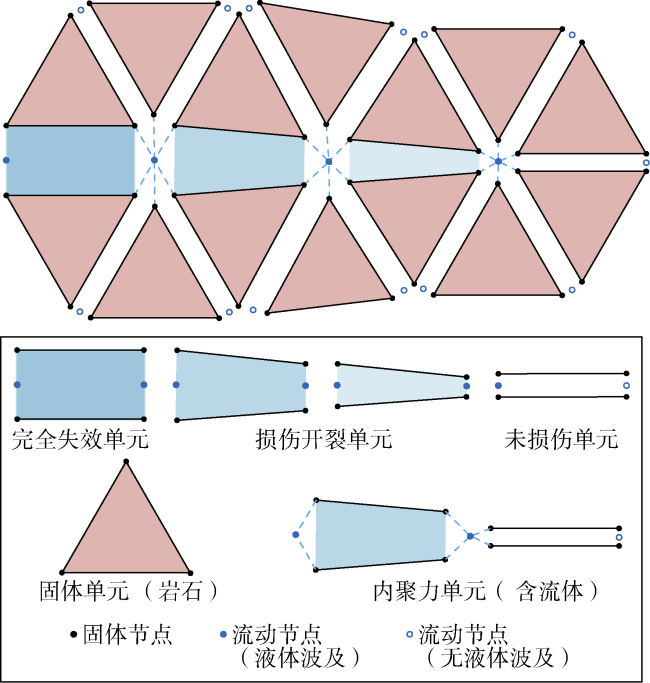
1.1 DFN-FEM复杂裂缝扩展理论
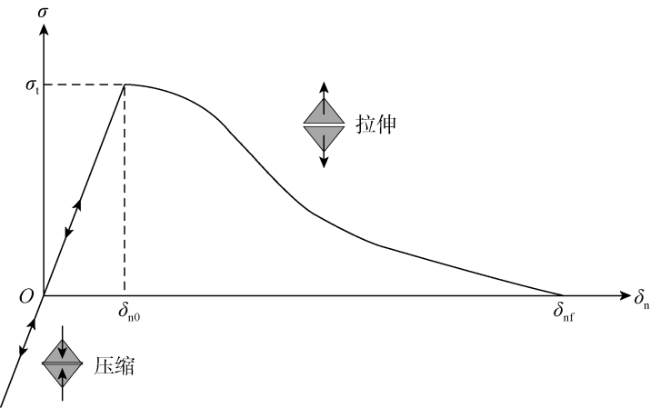
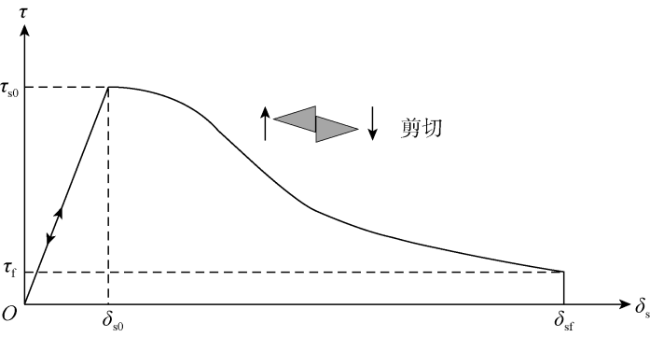
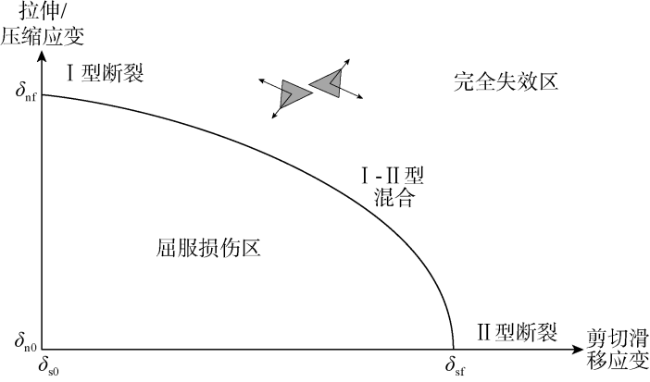
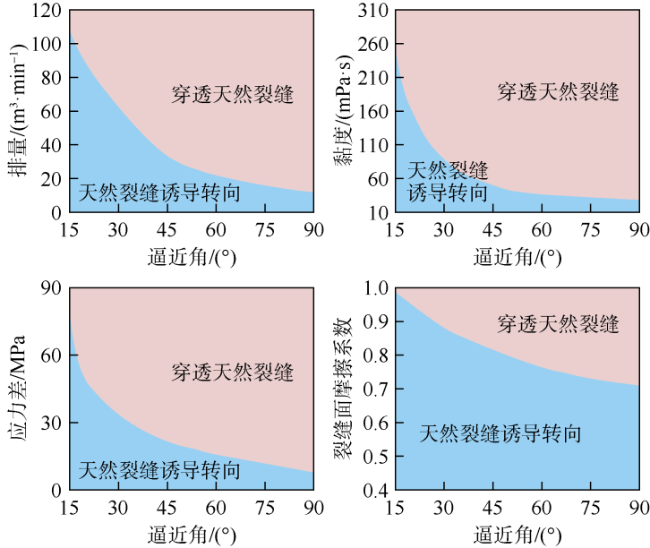
1.2 裂缝单元起裂及扩展非线性力学行为
1.3 裂缝单元内的流体流动
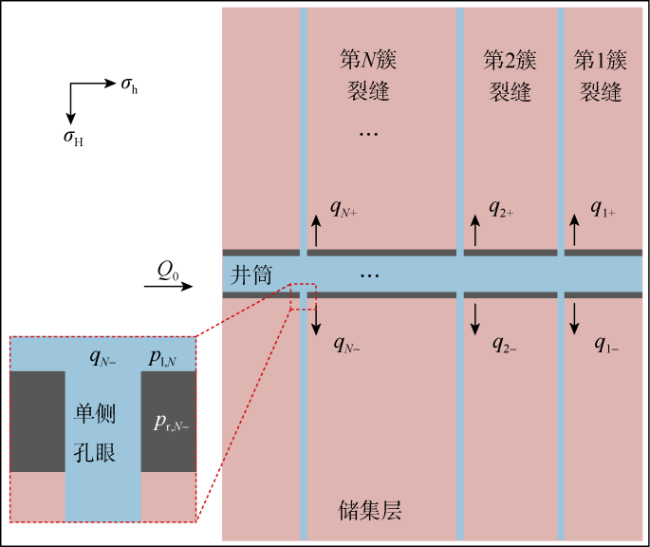
1.4 考虑孔眼冲蚀效应的多簇射孔压降模型
1.5 岩石基质单元变形
2 四川盆地深层页岩缝口暂堵压裂裂缝扩展模型
2.1 区域概况及建模基本参数
2.1.1 区块概况
2.1.2 基本地质力学参数
表1 水力压裂相关的储集层地质力学与施工参数 |
| 表征对象 | 参数名 | 参数值 |
|---|---|---|
| 岩石基质 | 弹性模量 | 25 GPa |
| 法向刚度 | 300 GPa/m | |
| 抗拉强度 | 3 MPa | |
| 拉伸断裂能 | 10 J/m2 | |
| 摩擦系数 | 0.6 | |
| 泊松比 | 0.234 | |
| 切向刚度 | 5 000 GPa/m | |
| 剪切强度 | 50 MPa | |
| 剪切断裂能 | 500 J/m2 | |
| 密度 | 2 600 kg/m3 | |
| 天然裂缝 | 法向刚度 | 300 GPa/m |
| 抗拉强度 | 1 MPa | |
| 拉伸断裂能 | 3 J/m2 | |
| 摩擦系数 | 0.4 | |
| 体积模量 | 2.2 GPa | |
| 切向刚度 | 3 000 GPa/m | |
| 剪切强度 | 20 MPa | |
| 剪切断裂能 | 50 J/m2 | |
| 密度 | 1 000 kg/m3 | |
| 地应力 | 最大水平主应力 | 67 MPa |
| 最小水平主应力 | 53 MPa |
2.1.3 天然裂缝分布
2.1.4 多簇体积压裂施工参数
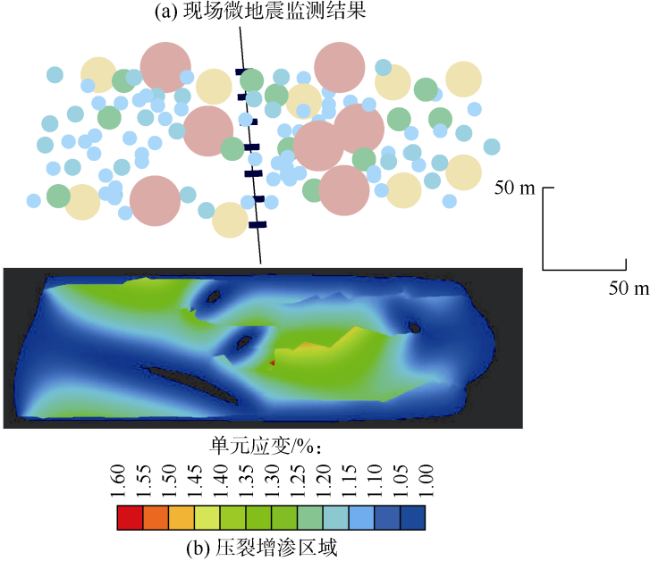
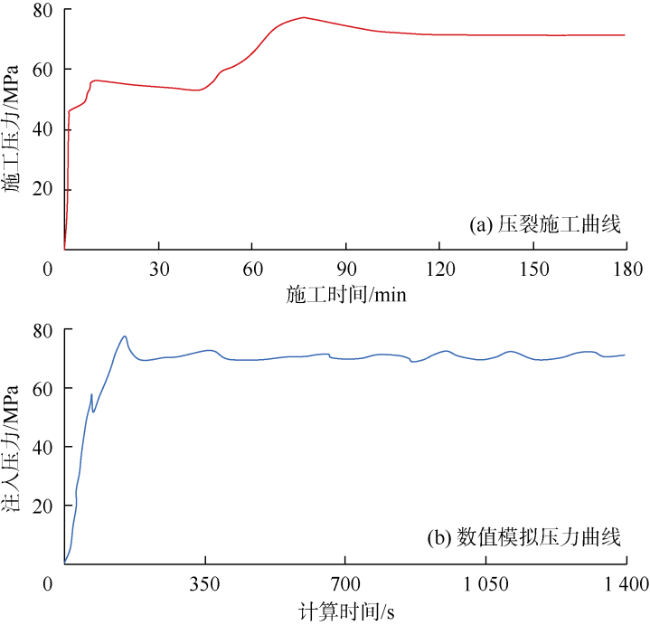
2.2 模型验证
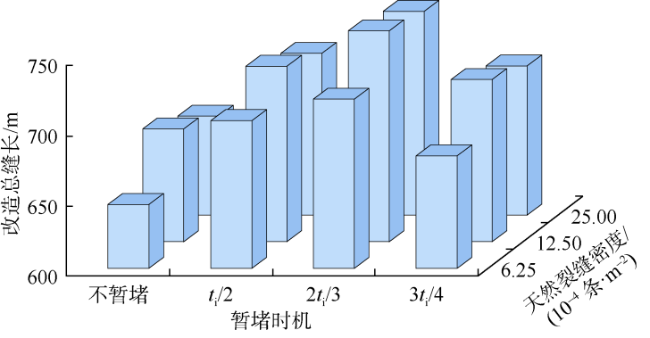
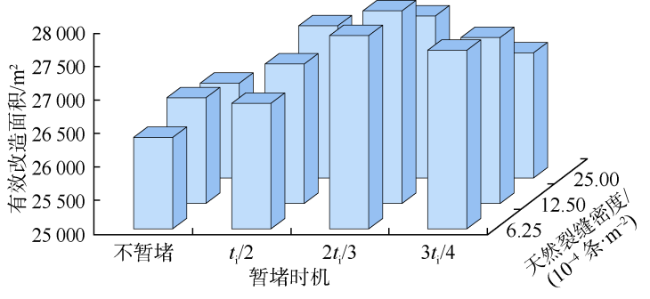
3 缝口暂堵裂缝扩展分析及暂堵时机优化
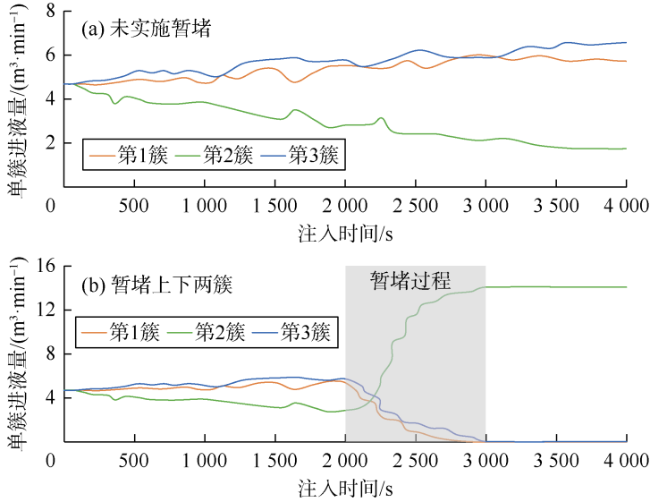
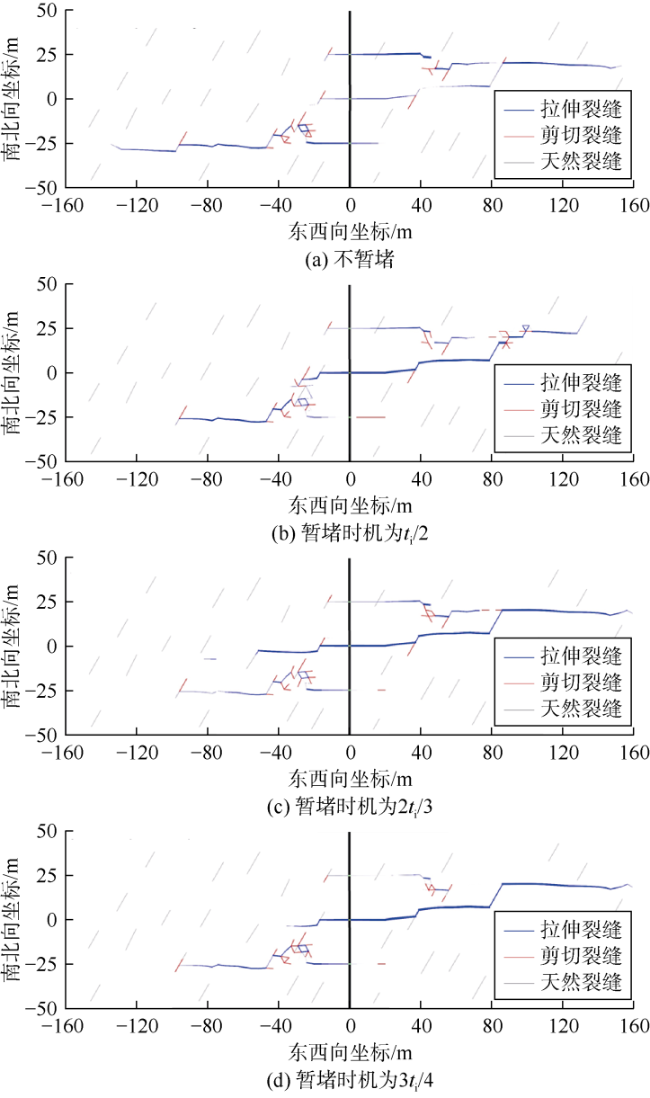
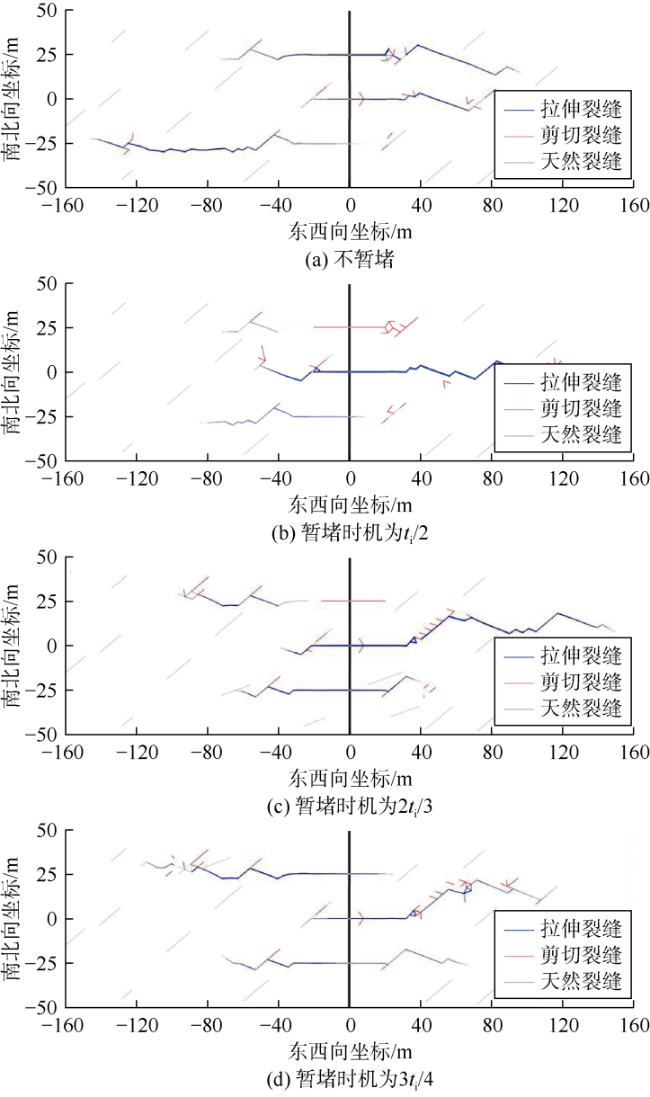
3.1 缝口暂堵对多簇裂缝扩展的影响
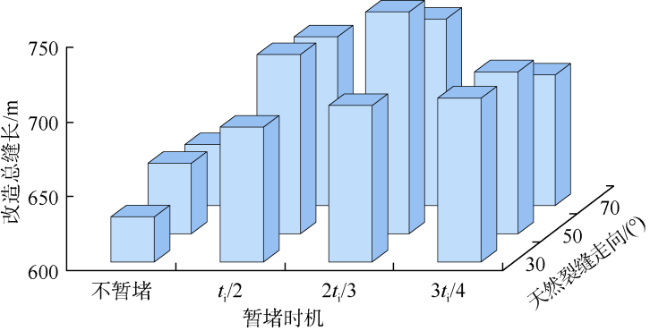
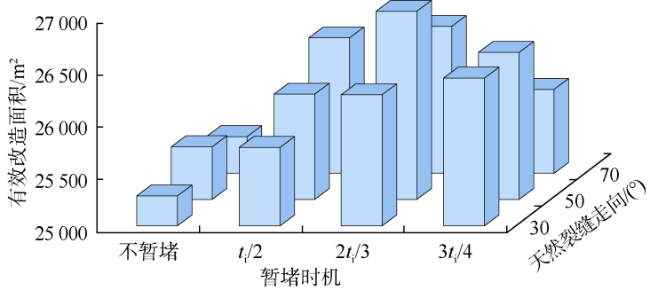
3.2 天然裂缝走向对暂堵时机的影响
3.3 天然裂缝密度对暂堵时机的影响
3.4 不同天然裂缝走向-密度组合下最优暂堵时机
表3 天然裂缝走向-密度的最优暂堵时机优化参数对照表 |
| 天然裂缝密度 | 不同天然裂缝走向下的暂堵时机 | ||
|---|---|---|---|
| 低 | 中 | 高 | |
| 低 | 2ti/3 | 2ti/3 | ti/2 |
| 中 | 3ti/4 | 2ti/3 | 2ti/3 |
| 高 | 3ti/4 | 2ti/3 | 2ti/3 |
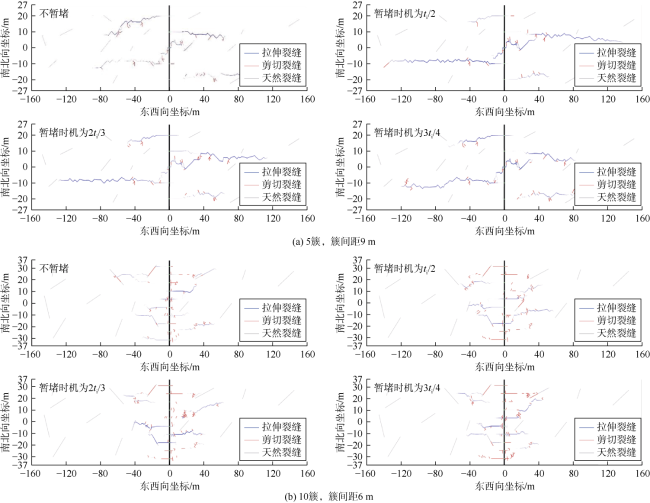
3.5 随机天然裂缝展布下的分簇方式适应性
4 现场应用
表4 威202A井组平台暂堵压裂对比测试参数统计表 |
| 井号 | 测试产量/ (104 m3·d-1) | 段均 簇数 | 用液强度/ (m3·m-1) | 加砂强度/ (t·m-1) | 是否 暂堵 |
|---|---|---|---|---|---|
| 202A-1 | 41.8 | 3.9 | 25.2 | 2.1 | 否 |
| 202A-2 | 40.2 | 3.4 | 25.8 | 2.0 | 否 |
| 202A-3 | 58.8 | 3.6 | 23.6 | 2.4 | 是 |
| 202A-4 | 51.5 | 3.5 | 24.5 | 2.5 | 是 |