0 引言
21世纪初形成了以连续管和超短半径水平井导向器为核心的超短半径水平井技术[1⇓-3]。该技术主要应用于老井二次完井和低产井增产改造[4⇓-6]。超短半径水平井射流钻井系统的井眼尺寸为25.4~50.1 mm,进尺可达到90 m。近年来,可旋转钻进柔性钻具的应用使超短半径水平井的井眼尺寸增加到114.0~142.0 mm,进尺为60~100 m[7⇓⇓-10]。超短半径水平井曲率半径为2~5 m,适用于139.7 mm和244.5 mm套管,在中国海上油田和煤层气田进行了多口井现场试验[7⇓-9,11]。虽然大尺寸的超短半径水平井裸眼能够匹配直径较大的筛管,但是完井筛管下入遇阻问题依然未能解决,因此超短半径水平井完钻后均采用裸眼完井。一种采用垂直于套管轴向方向割缝的筛管能够通过超短半径水平井的弯曲段,但是筛管在水平段的下入长度有限[12]。申瑞臣等[13-14]提出的煤层气水平井PE筛管泵送方案中聚乙烯（PE）筛管直径为50.8 mm,可以通过钻杆在水平段内泵送的PE筛管长度是570 m。柔性钻具结构复杂且内径较小,限制了可以通过其内部的非金属完井筛管尺寸。
笔者选用大尺寸非金属复合连续管加工筛管,同时采用小尺寸的钢质连续管作为内层管柱增强非金属复合连续管刚度。此外,设计采用液压驱动方式下入由非金属完井筛管与钢质连续管组成的完井管柱,克服完井管柱轴向力传递困难、管柱屈曲等问题。要实现液压驱动非金属筛管需要解决两个主要问题：一是设计适用于该技术的管柱结构与工具,二是将完井管柱的力学模型与液压驱动模型进行耦合。为了解决上述问题,首先需要进行完井管柱结构、井下专用装置和工艺设计,再将液压驱动模型引入完井管柱力学模型中。基于软绳模型[15-16]和刚性模型[17],GAO等[18⇓⇓-21]建立了井下管柱的局部及整体力学模型,对大位移井的管柱受力及屈曲行为进行了研究。还有学者对连续管的力学行为进行了研究[22],建立了连续管极限破坏模型[23],分析了连续管在水平井中的作业能力[24-25]。
1 管柱结构、配套工具及工作原理
针对超短半径水平井非金属完井筛管下入难题,进行了完井管柱结构优化设计,由内到外依次为导向管、液压驱动管、非金属复合连续筛管;同时,完成了液压驱动完井管柱配套工具设计,主要包括引鞋、导向管扶正器、滑动密封装置、转换短节等。其中,引鞋用于连接液压驱动管与非金属复合连续筛管,导向管扶正器用于保持导向管在液压驱动管内的居中度,滑动密封装置是维持液压驱动管与导向管之间滑动密封的核心装置,转换短节连接上部油管与下部完井管柱。完井管柱系统配合超短半径水平井液压驱动下入技术,引鞋液压载荷牵引完井管柱下入超短半径水平井,解决了超短半径水平井完井管柱推送下入过程中的轴向力传递困难、管柱屈曲等问题。
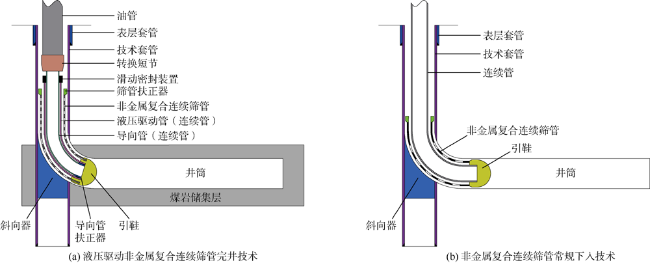
1.1 结构设计与工作原理
超短半径水平井柔性钻具通过斜向器沿不同方位在直井套管内自下而上依次侧钻[8],套管开窗长度约0.2 m,侧钻窗口间隔约0.6 m,完成目的层内多个井眼钻井[7]。在单个超短半径水平井眼完钻后起出柔性钻具,借助井底斜向器依次完成单个超短半径水平井眼的液压驱动完井管柱下入,完井管柱结构如图1 a所示。完井管柱由3层管柱组成：最外层是非金属复合连续筛管管柱,由引鞋、非金属复合连续筛管和筛管扶正器组成;中间层是液压驱动管柱,由液压驱动管（连续管）和滑动密封装置组成;最内层是导向管柱,由扶正器、导向管（连续管）组成。导向管柱通过转换短节与油管连接。在完井管柱下入至裸眼井段之前,液压驱动管、引鞋、导向管和转换短节通过滑动密封装置形成一个密封空间并充满空气。当转换短节内的滑套在液压作用下被打开后,完井管柱中的空气逐渐被液体置换,液压驱动管和非金属复合连续筛管在重力作用下向井底移动。液压驱动管和非金属复合连续筛管在水平井段遇阻时开启液压驱动完井管柱程序,通过导向管向液压驱动管传递液压,液压驱动管在液压动力下带动非金属复合连续筛管同步向井底移动。导向管在引导液压驱动管移动过程中始终与滑动密封装置保持滑动密封状态。同时,导向管与液压驱动管末端滑动密封装置之间的摩擦阻力可避免液压驱动管在垂直段发生螺旋屈曲。当液压驱动管末端滑动密封装置移动至导向管前端扶正器位置时制动,引鞋在液压作用下带动非金属复合连续筛管继续向前移动并剪切引鞋内的销钉与金属线,完成液压驱动管与引鞋分离。同时,引鞋内刀翼脱离金属线束缚后张开并固定于井壁,非金属复合连续筛管被固定于超短半径水平井内。地面泵压骤降表明引鞋与液压驱动管分离成功。然后,依次起出油管、导向管、液压驱动管柱与附件,完成单个超短半径水平井眼的非金属复合连续筛管液压驱动下入程序。该技术可在井眼直径116 mm的超短半径水平井裸眼内下入直径为100 mm、壁厚为20 mm的非金属复合连续筛管。
超短半径水平井非金属复合连续筛管常规下入技术如图1 b所示,采用连续管输送非金属复合连续筛管至水平井段,工艺简单,但是完井管柱下入过程中轴向力传递效率低、连续管与非金属复合连续筛管易发生屈曲,导致完井管柱下入长度有限。本文将通过工程案例计算对液压驱动非金属复合连续筛管完井技术和常规技术的下入长度进行对比。
1.2 关键装置
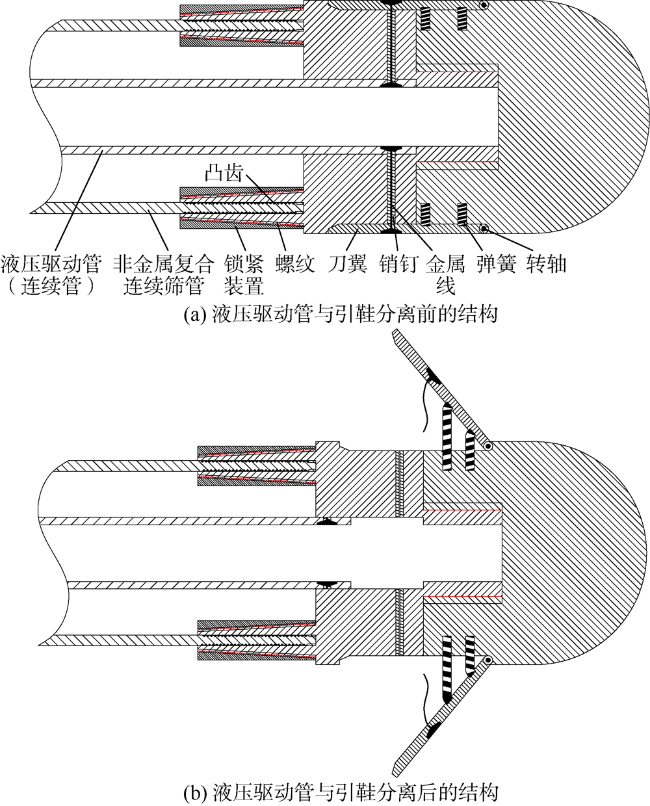
1.2.1 引鞋
引鞋本体采用轻质高强度的合金铝材料。将非金属复合连续筛管前端伸入引鞋凹槽内,通过锁紧装置与引鞋连接。液压驱动管、引鞋和刀翼由内置金属线的销钉连接。液压驱动管与引鞋分离前,4个刀翼收缩于引鞋本体内,如图2 a所示。液压驱动管与引鞋分离后,4个刀翼张开并固定于裸眼井壁,如图2 b所示。
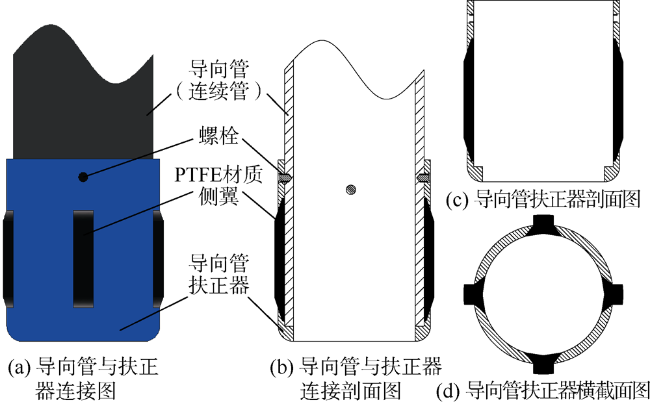
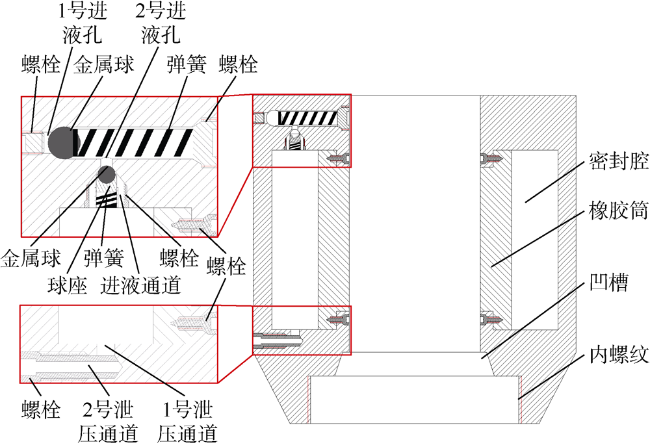
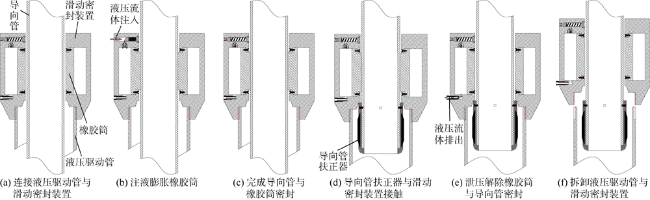
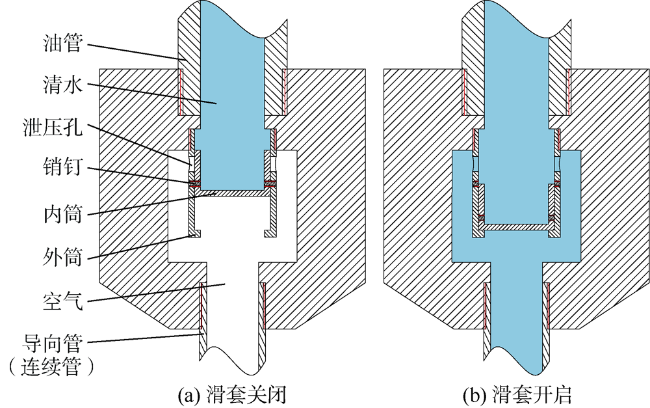
1.2.2 导向管扶正器与滑动密封装置
如图3 所示,导向管扶正器通过4个螺栓连接到导向管前端。4个凸翼采用低摩阻、耐磨损的聚四氟乙烯（PTFE）材质。扶正器保持导向管在斜向器位置居于液压驱动管的中心位置,以减小导向管与液压驱动管之间的摩擦阻力。
如图4 所示,滑动密封装置本体由调质钢制成,密封组件由橡胶制成,具有高强度、高韧性和高耐磨性。在井口处连接滑动密封装置和液压驱动管,如图5 a所示。液压流体经过1号和2号进液孔进入密封腔,胶筒在液压作用下膨胀并与导向管密封,如图5 b所示。当密封腔压力达到设计值时停止注入液压流体,1号和2号进液孔内金属密封球在弹簧弹力作用下复位,然后关闭1号和2号进液孔,如图5 c所示。滑动密封装置与导向管扶正器接触后液压驱动管制动,如图5 d所示。液压驱动非金属复合连续筛管完井作业完成后起出液压驱动装置至井口,打开泄压通道释放密封腔内的压力使橡胶复位,如图5 e所示。拆卸液压驱动管上端滑动密封装置,如图5 f所示。
1.2.3 转换短节与非金属复合连续筛管
在完井管柱的引鞋到达套管侧钻位置前,转换短节内置的滑套装置保持关闭,转换短节下部完井管柱内充满空气,上部油管内充满清水,如图6 a所示。引鞋到达套管侧钻位置后向油管内注入清水,滑套在液压作用下打开后停泵,如图6 b所示。转换短节上部油管内清水进入完井管柱内驱替空气过程中,液压驱动管和非金属复合连续筛管在重力作用下向井底移动。
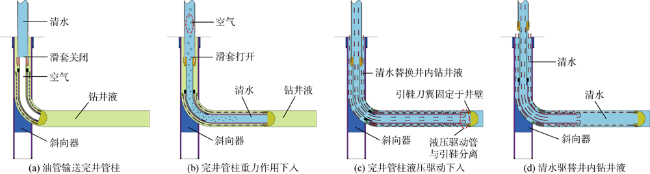
1.3 液压驱动非金属复合连续筛管完井流程
①转换短节下端完井管柱形成的密封空间内充满空气,转换短节上端油管充满清水,采用油管输送完井管柱至套管侧钻位置,如图8 a所示。②采用液压方式打开转换短节内置的滑套,滑套打开后立即停泵,上部油管柱内的清水进入完井管柱内驱替空气过程中,非金属复合连续筛管和液压驱动管在重力作用下向井底移动直至遇阻,如图8 b所示。③启动液压驱动非金属复合连续筛管程序,滑动密封装置到达导向管扶正器位置时液压驱动管发生制动。引鞋与非金属复合连续筛管在液压驱动下继续移动并剪切引鞋内置销钉,液压驱动管与引鞋分离。同时,刀翼张开并将非金属复合连续筛管固定于井壁,如图8 c所示。④通过作业管柱向井内注入清水驱替钻井液,减少钻井液对储集层伤害,如图8 d所示。
2 管柱力学-液压耦合模型
针对液压驱动管和非金属复合连续筛管组成的完井管柱结构,将帕斯卡原理和液压驱动原理引入管柱力学模型,建立管柱力学-液压耦合模型。以超短半径水平井的井身结构、管柱强度、工作泵的安全工作压力、管柱临界下入速度等作为约束条件,采用有限差分法求解超短半径水平井液压驱动非金属复合连续筛管下入长度。
2.1 管柱力学模型
假设条件：①完井管柱采用软杆模型;②柔性管柱的外侧与井壁充分接触;管柱与井壁的曲率相同;③忽略管柱上的剪切力;④将靠近井口的管柱末端称为后端,靠近井底的管柱末端称为前端。
2.1.1 管柱轴向力与侧向力
超短半径水平井弯曲井段相对水平进尺较短,简化为二维井眼轨迹计算完井管柱的轴向力与侧向力载荷。
完井管柱轴向力的计算公式为[32]：
$\text{d}{{T}_{i}}=\left[ \left( \mu \sin {{\theta }_{i}}-\cos {{\theta }_{i}} \right)\rho g{{A}_{\text{c}}}+{{f}_{\text{c}i}} \right]\text{d}{{l}_{i}}$ （i=1,2,…,n+1）
${{T}_{i}}=E{{A}_{\text{c}}}\frac{\partial {{u}_{i}}}{\partial {{l}_{i}}}$
由（1）式、（2）式可得：
$\frac{{{\partial }^{2}}{{u}_{i}}}{\partial {{l}_{i}}^{2}}=\frac{\left( \mu \sin {{\theta }_{i}}-\cos {{\theta }_{i}} \right)\rho {{A}_{\text{c}}}g+{{f}_{\text{c}i}}}{E{{A}_{\text{c}}}}$
（3）式的有限差分格式为：
$u_{i+1,j}^{{}}-2u_{i,j}^{{}}+u_{i-1,j}^{{}}=\frac{\left( \mu \sin {{\theta }_{i,j}}-\cos {{\theta }_{i,j}} \right)\rho {{A}_{\text{c}}}g+{{f}_{\text{c}i,j}}}{E{{A}_{\text{c}}}}\text{d}{{l}^{2}}$ （j=1,2,…,m）
其中,当i=1且j≠1时,fci,j=Fc/dli,否则fci,j=0。
有限差分计算的初始条件为：
$u_{0,j}^{{}}=j\text{d}l$
边界条件为：
$EA\frac{u_{n+1,j}^{{}}-u_{n,j}^{{}}}{\text{d}l}=\left\{ \begin{matrix} 0\quad \quad \quad \quad j=1 \\ {{T}_{\text{r}}}\left( j-1 \right)\quad j\ne 1 \\ \end{matrix} \right.$
完井管柱侧向力的计算公式为[15]：
${{F}_{\text{n}}}=\sqrt{{{\left( \text{d}T\Delta \alpha \sin \overline{\theta } \right)}^{2}}+{{\left( \text{d}T\Delta \theta +W\sin \overline{\theta } \right)}^{2}}}$
完井管柱与井壁之间摩擦力的计算公式为：
${{F}_{\text{d}}}={{F}_{\text{n}}}\mu $
2.1.2 滑动密封装置与引鞋受力
滑动密封装置与引鞋处的液压相等但方向相反,其内外压差形成的力与管柱轴线重合。引鞋和滑动密封装置受力的计算公式分别为：
$F\text{=}\frac{\text{ }\!\!\pi\!\!\text{ }{{p}_{\text{s}}}\left( {{d}_{\text{hi}}}^{2}-{{d}_{\text{go}}}^{2} \right)}{4}$
${{F}_{\text{s}}}=\frac{\text{ }\!\!\pi\!\!\text{ }{{p}_{\text{s}}}d{{_{\text{hi}}^{{}}}^{2}}}{4}$
滑动密封装置橡胶筒与导向管之间滑动摩擦力的计算公式为：
${{F}_{\text{c}}}={{N}_{\text{c}}}{{\mu }_{\text{c}}}=ql-{{F}_{\text{hel}}}$
2.2 液压驱动模型
假设条件：①流体体积不可压缩;②整个管柱处于理想密封状态;③地层无漏失;④摩擦力为库仑摩擦力;⑤不考虑流体在管柱中流动的局部压力损失;⑥管柱内的流体为清水。
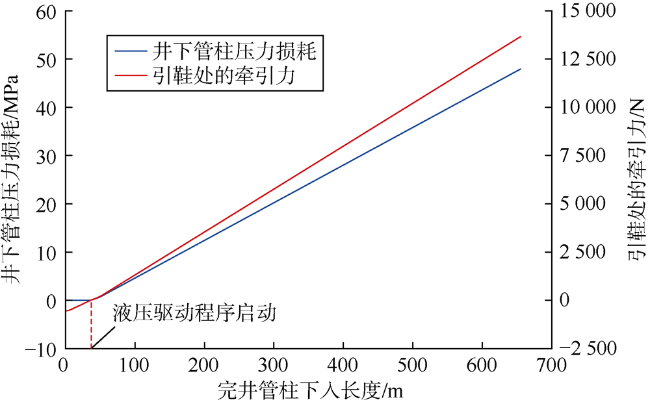
2.2.1 驱动完井管柱的液压载荷
驱动完井管柱下入的牵引力的计算公式为：
${{T}_{\text{r}}}={{F}_{\text{c}}}+{{F}_{\text{d}}}-{{W}_{\text{p}}}$
该牵引力等于作用于引鞋处的液压载荷,则引鞋处液压的计算公式为：
${{p}_{\text{s}}}=\frac{{{T}_{\text{r}}}}{{{A}_{\text{h}}}}$
2.2.2 管柱系统压力损耗
基于流体连续性方程,计算不同管径下流体平均速度：
${{v}_{1}}{{A}_{1}}={{v}_{2}}{{A}_{2}}={{q}_{\text{f}}}$
其中 ${{A}_{1}}=\frac{\text{ }\!\!\pi\!\!\text{ }{{d}_{1}}^{2}}{4}$ ${{A}_{2}}=\frac{\text{ }\!\!\pi\!\!\text{ }{{d}_{2}}^{2}}{4}$
由于液压驱动非金属完井管柱中采用的清水近似为牛顿流体,管内流体的雷诺数计算公式为：
$R{{e}_{1}}=\frac{{{v}_{1}}{{d}_{1}}{{\rho }_{\text{f}}}}{\gamma }$
$R{{e}_{2}}=\frac{{{v}_{2}}{{d}_{2}}{{\rho }_{\text{f}}}}{\gamma }$
管柱内液体流动摩擦系数计算公式为[33]：
${{f}_{1}}=\frac{a}{R{{e}_{\text{1}}}^{b}}$
${{f}_{2}}=\frac{a}{R{{e}_{2}}^{b}}$
式中,当Re1≤2 000或Re2≤2 000时,a=16,b=1;当Re1>2 000或Re2>2 000时,a=0.078 6,b=0.25。
流体在管柱内流动产生的压力损耗[34]为：
$\Delta p=\frac{2{{f}_{1}}{{\rho }_{\text{f}}}{{l}_{1}}{{v}_{1}}^{2}}{{{d}_{1}}}\text{+}\frac{2{{f}_{2}}{{\rho }_{\text{f}}}{{l}_{2}}{{v}_{2}}^{2}}{{{d}_{2}}}$
2.3 约束条件
需要考虑的约束条件主要包括：管柱螺旋屈曲临界载荷、工作泵的安全工作压力（本文取48.0 MPa）、完井管柱临界下入速度、连续管最小弯曲半径、完井管柱米塞斯强度校核、超短半径水平井井身结构与曲率半径。
忽略管柱正弦屈曲引起的附加摩擦力的影响,直井段管柱螺旋屈曲临界载荷计算公式为[35]：
${{F}_{\text{hel}}}=5.55{{\left( EI{{q}^{2}} \right)}^{\frac{1}{3}}}$
弯曲井段管柱螺旋屈曲临界载荷计算公式为[36]：
${{F}_{\text{hel}}}=\frac{12EI}{{{r}_{\text{c}}}R}\left( 1+\sqrt{1+\frac{{{r}_{\text{c}}}{{R}^{2}}q\sin \theta }{8EI}} \right)$
水平井段管柱螺旋屈曲载荷计算公式为[37]：
${{F}_{\text{hel}}}=2\left( 2\sqrt{2}-1 \right)\sqrt{\frac{EIq\sin \theta }{{{r}_{\text{c}}}}}$
完井管柱高速运动时突然遇阻可能会导致管柱发生螺旋屈曲甚至自锁。利用水平段液压驱动管的螺旋屈曲临界载荷计算连续管在液压驱动过程中的临界下入速度：
$v\le C\sqrt{\frac{2}{\rho E}}\frac{{{F}_{\text{hel}}}}{{{A}_{\text{c}}}}$
液压驱动管与导向管均为连续管,在弹性变形范围内的最小弯曲半径可利用下式进行计算：
$d=\frac{2{{R}_{\min }}{{\sigma }_{\text{s}}}}{E}$
3 工程案例计算分析
2017年,在鄂尔多斯盆地东缘1口深层煤层气直井进行了侧钻超短半径水平井试验。该井生产套管外径139.7 mm,厚度7.72 mm,下入深度1 968.1 m。该井在1 900.0 m处侧钻,井眼直径114.0 mm,水平进尺100.0 m,采用裸眼完井。基于该井的井身结构数据与本文提出的管柱力学-液压耦合模型,计算液压驱动完井管柱下入长度。为量化评价液压驱动完井管柱最大下入长度,假设该超短半径水平井的水平进尺为无限区间。
3.1 超短半径水平井完井管柱结构设计
表1 液压驱动管与导向管组合方案 |
| 编号 | 完井管柱结构 | 钢级 | 材质 | 屈服强度/kPa | 弹性模量/kPa | 密度/(kg•m-3) | 外径/mm | 内径/mm | 最小弹性弯曲半径/m |
|---|---|---|---|---|---|---|---|---|---|
| 1# | 导向管 | CT-90 | A-606Type4MOD | 620 528.2 | 206 842 719.8 | 7 849 | 19.05 | 14.05 | 4.8 |
| 液压驱动管 | CT-100 | A-606Type4MOD | 689 475.7 | 206 842 719.8 | 7 849 | 31.75 | 27.69 | ||
| 2# | 导向管 | CT-90 | A-606Type4MOD | 620 528.2 | 206 842 719.8 | 7 849 | 12.70 | 7.70 | 3.8 |
| 液压驱动管 | CT-100 | A-606Type4MOD | 689 475.7 | 206 842 719.8 | 7 849 | 25.40 | 21.34 | ||
| 3# | 导向管 | CT-90 | A-606Type4MOD | 620 528.2 | 206 842 719.8 | 7 849 | 12.70 | 7.70 | 3.2 |
| 液压驱动管 | CT-100 | A-606Type4MOD | 689 475.7 | 206 842 719.8 | 7 849 | 19.05 | 14.05 |
3.2 数值计算
3.2.1 常规技术非金属复合连续筛管下入长度
基本参数：钻井液密度为1 050 kg/m3;清水密度为1 000 kg/m3,黏度为1.000 5 mPa·s。
连续管尺寸、超短半径水平井曲率半径、非金属复合连续筛管与井壁间摩擦系数是影响常规技术非金属复合连续筛管下入长度的主要因素。基于这3个因素进行正交分析设计,如表2 所示。在正交分析设计的基础上进行数值计算,将影响下入长度的3个主要因素作为自变量,最大下入长度作为评价指标,得到数值计算结果,如表3 所示。
表2 常规技术非金属复合连续筛管下入长度影响因素的正交分析设计 |
| 水平 | 因素 | ||
|---|---|---|---|
| 连续管尺寸/mm | 井眼曲率半径/m | 摩擦系数 | |
| 1 | 19.05 | 3.2 | 0.2 |
| 2 | 25.40 | 3.8 | 0.3 |
| 3 | 31.75 | 4.8 | 0.4 |
表3 常规技术非金属复合连续筛管下入长度数值计算结果 |
| 序号 | 连续管尺寸/mm | 井眼曲率半径/m | 摩擦系数 | 最大下入长度/m |
|---|---|---|---|---|
| 1 | 19.05 | 3.20 | 0.20 | 25 |
| 2 | 19.05 | 3.80 | 0.30 | 15 |
| 3 | 19.05 | 4.80 | 0.40 | 11 |
| 4 | 25.40 | 3.20 | 0.30 | 18 |
| 5 | 25.40 | 3.80 | 0.40 | 12 |
| 6 | 25.40 | 4.80 | 0.20 | 32 |
| 7 | 31.75 | 3.20 | 0.40 | 13 |
| 8 | 31.75 | 3.80 | 0.20 | 36 |
| 9 | 31.75 | 4.80 | 0.30 | 21 |
对数值计算结果进行极差分析,如表4 所示。可以看出,对常规技术非金属复合连续筛管下入长度的影响由大到小依次为摩擦系数、连续管尺寸和井眼曲率半径。对数值计算结果进行方差分析,如表5 所示。可以看出,摩擦系数对常规技术非金属复合连续筛管下入长度影响最显著,连续管尺寸和井眼曲率半径的影响相对不显著。基于极差分析和方差分析结果,摩擦系数为0.2时,采用直径为31.75 mm的连续管,在曲率半径为4.8 m的超短半径水平井内,常规技术非金属复合连续筛管最大下入长度为37 m。
表4 常规技术非金属复合连续筛管下入长度数值计算结果的极差分析 |
| 因素 | K1/m | K2/m | K3/m | k1/m | k2/m | k3/m | r/m |
|---|---|---|---|---|---|---|---|
| 连续管尺寸 | 51 | 62 | 70 | 17.00 | 20.67 | 23.33 | 6.33 |
| 井眼曲率半径 | 56 | 63 | 64 | 18.67 | 21.00 | 21.33 | 2.67 |
| 摩擦系数 | 93 | 54 | 36 | 31.00 | 18.00 | 12.00 | 19.00 |
注：K1,K2,K3分别为某因素在水平1,2,3下的最大下入长度之和,以连续管尺寸的水平1（19.05 mm）为例,K1=25+15+11=51 m;k1,k2,k3分别为某因素在水平1,2,3下的最大下入长度的平均值,以连续管尺寸的水平1（19.05 mm）为例,k1=K1/3=17 m;r为极差,r= max(k1,k2,k3)-min(k1,k2,k3) |
表5 常规技术非金属复合连续筛管下入长度数值计算结果的方差分析 |
| 方差来源 | 离差平方和 | 自由度 | 均方 | 显著性差异水平值 | 显著性 |
|---|---|---|---|---|---|
| 连续管尺寸 | 60.67 | 2 | 30.33 | 7.00 | 不显著 |
| 井眼曲率半径 | 12.67 | 2 | 6.33 | 1.46 | 不显著 |
| 摩擦系数 | 566.00 | 2 | 283.00 | 65.31 | 显著 |
| 误差 | 8.67 | 2 | 4.33 | ||
| 总和 | 648.01 | 8 | 323.99 |
3.2.2 液压驱动非金属复合连续筛管下入长度
基本参数：钻井液密度为1 050 kg/m3;清水密度为1 000 kg/m3,黏度为1.000 5 mPa·s;井眼曲率半径为4.8 m,采用外径为60.3 mm的油管输送完井管柱至直井套管侧钻开窗位置。
完井管柱结构、注入流量、非金属复合连续筛管与井筒间摩擦系数是影响液压驱动非金属复合连续筛管下入长度的主要因素。基于这3个因素进行正交分析设计,如表6 所示。在正交分析设计的基础上进行数值计算,将影响下入长度的3个主要因素作为自变量,最大下入长度作为评价指标,得到数值计算结果,如表7 所示。
表6 液压驱动非金属复合连续筛管下入长度影响因素的正交分析设计 |
| 水平 | 因素 | ||
|---|---|---|---|
| 完井管柱结构 | 注入流量/(L·min-1) | 摩擦系数 | |
| 1 | 1# | 1 | 0.2 |
| 2 | 2# | 3 | 0.3 |
| 3 | 3# | 6 | 0.4 |
表7 液压驱动非金属复合连续筛管下入长度数值计算结果 |
| 序号 | 完井管柱结构 | 注入流量/(L·min-1) | 摩擦系数 | 最大下入长度/m |
|---|---|---|---|---|
| 1 | 1# | 1 | 0.2 | 655 |
| 2 | 1# | 3 | 0.3 | 510 |
| 3 | 1# | 6 | 0.4 | 379 |
| 4 | 2# | 1 | 0.3 | 301 |
| 5 | 2# | 3 | 0.4 | 228 |
| 6 | 2# | 6 | 0.2 | 381 |
| 7 | 3# | 1 | 0.4 | 250 |
| 8 | 3# | 3 | 0.2 | 427 |
| 9 | 3# | 6 | 0.3 | 333 |
对数值计算结果进行极差分析,如表8 所示。可以看出,完井管柱结构对液压驱动非金属复合连续筛管下入长度的影响最大,其次为摩擦系数,注入流量影响最小。对数值计算结果进行方差分析,如表9 所示。可以看出,摩擦系数和完井管柱结构对液压驱动非金属复合连续筛管下入长度有显著影响,注入流量的影响相对不显著。基于极差分析和方差分析结果,采用1#完井管柱结构,摩擦系数为0.2,注入流量为1 L/min的条件下,超短半径水平井液压驱动非金属复合连续筛管最大下入长度为655.0 m。
表8 液压驱动非金属复合连续筛管下入长度数值计算结果的极差分析 |
| 因素 | K1/m | K2/m | K3/m | k1/m | k2/m | k3/m | r/m |
|---|---|---|---|---|---|---|---|
| 完井管柱结构 | 1 544 | 910 | 1 010 | 514.67 | 303.33 | 336.67 | 211.33 |
| 注入流量 | 1 206 | 1 165 | 1 093 | 402.00 | 388.33 | 364.33 | 37.67 |
| 摩擦系数 | 1 463 | 1 144 | 857 | 487.67 | 381.33 | 285.67 | 202.00 |
表9 液压驱动非金属复合连续筛管下入长度数值计算结果的方差分析 |
| 方差来源 | 离差平方和 | 自由度 | 均方 | 显著性差异 水平值 | 显著性 |
|---|---|---|---|---|---|
| 完井管柱结构 | 77 456.89 | 2 | 38 728.44 | 37.35 | 显著 |
| 注入流量 | 2 181.56 | 2 | 1 090.78 | 1.05 | 不显著 |
| 摩擦系数 | 61 262.89 | 2 | 30 631.44 | 29.54 | 显著 |
| 误差 | 2 073.56 | 2 | 1 036.78 | ||
| 总和 | 142 974.89 | 8 | 71 487.44 |
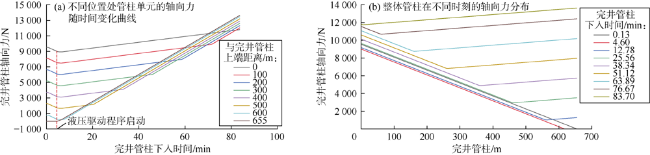
3.3 液压驱动完井管柱结构适用条件分析
表10 液压驱动完井管柱结构适用条件 |
| 侧钻套管 尺寸/mm | 裸眼尺寸/ mm | 非金属复合连续 筛管外径/mm | 完井管柱 结构 | 液压驱动管 外径/mm | 导向管外径/ mm | 井眼曲率 半径/m | 完井管柱临界下入 速度/(m·min-1) | 液压驱动注入 流量/(L·min-1) | 最大下入 长度/m |
|---|---|---|---|---|---|---|---|---|---|
| 139.7 | ≥114 | ≥100 | 1# | 31.75 | 19.05 | ≥4.8 | 39.81 | 1.50~7.54 | 655 |
| 2# | 25.40 | 12.70 | ≥3.8 | 31.35 | 0.50~4.67 | 381 |
3.4 完井管柱力学与水力学分析
基本参数：采用表1 中1#完井管柱结构,井眼曲率半径为4.8 m;钻井液密度为1 050 kg/m3;清水密度为1 000 kg/m3,黏度为1.000 5 mPa·s;非金属复合连续筛管与井壁间摩擦系数为0.2;采用外径为60.3 mm的油管输送完井管柱至直井套管侧钻开窗位置;液压驱动完井管柱的注入排量为1.5 L/min。
基于本文提出的管柱力学-液压耦合模型,采用有限差分法计算超短半径水平井液压驱动非金属复合连续筛管下入长度和井下管柱压力损耗。超短半径水平井液压驱动完井管柱下入过程中受到的牵引力与井下管柱压力损耗如图9 所示。液压驱动管和非金属复合连续筛管依靠自重下入超短半径水平井内36 m后遇阻,此过程泵压为零。液压驱动完井管柱程序启动后引鞋处牵引力逐渐增大,完井管柱克服摩擦阻力后继续向井底移动,井下管柱压力损耗达到48 MPa时,牵引力达到13 663.06 N,完井管柱最大下入长度为655 m。
在超短半径水平井液压驱动完井管柱下入过程中,距离完井管柱上端不同位置处管柱单元的轴向力随时间变化如图10 a所示,整体完井管柱在不同时刻的轴向力分布如图10 b所示。液压驱动完井管柱程序启动前,完井管柱依靠自重下入水平井段,完井管柱轴向力逐渐减小,摩擦阻力逐渐增大,进入水平段的完井管柱从拉伸状态进入受压状态。液压驱动完井管柱程序启动后,完井管柱前端引鞋处牵引力逐渐增大,完井管柱克服与井筒之间摩擦阻力向井底移动,完井管柱逐渐由受压状态进入拉伸状态,完井管柱下入过程中未发生螺旋屈曲。
4 结论
优化了超短半径水平井液压驱动非金属复合连续筛管完井技术的完井管柱结构,由内到外依次为导向管、液压驱动管、非金属复合连续筛管;完成了配套装置设计,主要包括引鞋、导向管扶正器、滑动密封装置、转换短节等。完井管柱系统配合超短半径水平井液压驱动下入技术,能够实现在超短半径水平井中下入非金属复合连续筛管,保持井眼稳定性。建立了管柱力学-液压耦合模型,将水力学模型引入管柱力学模型,可为超短半径水平井液压驱动非金属连续筛管下入技术设计与控制提供理论指导。
以某煤层气超短半径水平井的井身结构为基础,应用管柱力学-液压耦合模型进行数值计算后得出,采用常规技术下入非金属复合连续筛管的最大下入长度为37 m,而相同条件下液压驱动非金属复合连续筛管最大下入长度可达655 m,大幅度延长了管柱下入长度。数值计算结果多因素正交分析表明,完井管柱结构和非金属复合连续筛管与井筒间摩擦系数是对超短半径水平井液压驱动非金属复合连续筛管下入长度影响最大的两个因素。
优选了两种适用于不同条件的超短半径水平井液压驱动完井管柱结构,数值计算得出两种完井管柱结构的最大下入长度分别为381,655 m。
符号注释：
a,b——计算系数;A1——油管内截面积,m2;A2——导向管内截面积,m2;Ac——完井管柱截面积,m2;Ah——液压驱动管内截面积,m2;C——安全系数,0.7≤C≤1.0,无因次;d——连续管的外径,m;d1——油管内径,m;d2——导向管内径,m;dgo——导向管外径,m;dhi——液压驱动管内径,m;E——完井管柱弹性模量,Pa;f1——油管内流体流动时的摩擦系数,无因次;f2——导向管内流体流动时的摩擦系数,无因次;fc——单位长度的滑动摩擦力,N/m;F——引鞋受力,N;Fc——滑动摩擦力,N;Fd——完井管柱与井筒之间的摩擦力,N;Fhel——完井管柱临界屈曲载荷,N;Fn——完井管柱微元的侧向力,N;Fs——滑动密封装置受力,N;g——重力加速度,m/s2;i——节点序号;I——完井管柱的截面惯性矩,m4;j——微元序号;l——完井管柱长度（超短半径水平井进尺）,m;dl——均匀离散后的完井管柱微元长度,m;l1——油管长度,m;l2——导向管长度,m;m——微元数量;n——节点数量;Nc——橡胶作用于导向管本体上的正压力,N;ps——引鞋处的液压,Pa;Δp——整体管柱内流体流动产生的压力损耗,Pa;q——单位长度完井管柱的重力,N/m;qf——液压驱动非金属复合连续筛管的流量,m3/s;rc——完井管柱与井眼之间的间隙,m;R——井眼曲率半径,m;Rmin——连续管的最小弹性弯曲半径,m;Re1——油管内流体雷诺数,无因次;Re2——导向管内流体雷诺数,无因次;T——完井管柱轴向拉力,N;dT——完井管柱微元轴向拉力,N;Tr——牵引力,N;u——完井管柱伸长量,m;v1——油管内液体平均流速,m/s;v2——导向管内液体平均流速,m/s;v——完井管柱下入速度,m/s;W——完井管柱微元在完井液中的浮重,N;Wp——完井管柱在钻井液中的浮重,N;Δα——微元段的方位角增量,Δα=0,rad;γ——注入流体的黏度,Pa·s;θ——井斜角,rad;Δθ——井斜角增量,rad; $\bar{\theta }$——微元段的平均井斜角,rad;μ——非金属复合连续筛管与井壁之间的滑动摩擦系数,无因次;μc——橡胶与导向管之间的滑动摩擦系数,无因次;ρ——完井管柱密度,kg/m3;ρf——注入流体的密度,kg/m3;σs——连续管的屈服强度,Pa。