0 引言
目前普遍通过优化水泥环力学性能来保障水泥环的力学和密封完整性[4-5]：初纬等[6]通过建立弹塑性力学模型分析了套管内压变化对水泥环力学完整性的影响,研究发现,水泥环将在套管内压加载阶段发生塑性屈服,并在卸载阶段引发界面剥离和微环隙问题。除了塑性屈服,Liu等研究发现,水泥环还易受压裂载荷影响而发生拉伸破坏并引发力学完整性失效,采用低弹性模量、高泊松比的水泥环能够有效避免其屈服破坏,并降低微环隙风险产生[7-8]。李勇等[9]为评价压裂载荷下的水泥环界面密封完整性,建立了理论模型,并发现水泥环泊松比对界面裂缝扩展长度呈非线性影响,提高水泥环弹性模量有利于缩短界面裂缝扩展长度。Fan等[5]的研究也明确指出提高水泥环弹性模量和胶结强度有利于缩短界面裂缝的扩展长度。Wang等[10]则发现水泥环弹性模量对界面裂缝宽度呈现先增大后降低的非线性影响。
可以发现,不同水泥环失效形式下对水泥环力学性能参数指标的要求不同,如何合理设计力学性能参数是保障水泥环力学完整性和界面密封完整性的关键。针对上述问题,本文基于三向应力下的水泥环弹塑性模型和界面裂缝应力场模型,综合考虑水泥环拉伸破坏、塑性屈服、界面裂缝沿界面扩展以及界面裂缝曲折扩展等失效形式,建立了井筒密封评判与水泥环力学性能设计方法。采用该方法,以大港油田页岩油GD水平井为例开展了压裂工况下的井筒密封失效分析,明确了水泥环强度、弹性模量和泊松比对不同失效形式的影响规律,提出了保障GD井压裂水泥环力学完整性和密封完整性要求的力学性能量化指标。
1 井筒水泥环应力分析
1.1 弹塑性水泥环应力分析
假设套管居中且套管和地层为均质弹性体,水泥环为均质弹塑性体。定义拉应力为正、压应力为负,并认为压裂过程中的水泥环应力状态是压裂载荷引起的应力变化在初始应力状态上的叠加[11]。
1.1.1 弹塑性水泥环的应力与位移分析
压裂过程中,水泥环承受径向（σr）、周向（σθ）和轴向（σz）应力,其中,径向应力显著高于周向应力,轴向应力居于径向和周向应力之间,如图1 所示。
考虑井筒水泥环三向应力大小及分布规律,以双剪统一强度理论[12]为屈服准则（（1）式）,建立水泥环弹塑性力学模型。
$\frac{1}{\alpha }{{\sigma }_{\text{r}}}-\frac{1}{1+b}\left( b{{\sigma }_{\text{z}}}+{{\sigma }_{\text{ }\!\!\theta\!\!\text{ }}} \right)\text{=}{{\sigma }_{\text{c}}}$
为简化推导过程,认为 ${{\sigma }_{\text{z}}}=\left( {{\sigma }_{\text{r}}}+{{\sigma }_{\text{ }\!\!\theta\!\!\text{ }}} \right)/2$。同时,水泥环在径向和周向上的应力分量满足平衡方程：
$\frac{\text{d}{{\sigma }_{\text{r}}}}{\text{d}r}+\frac{{{\sigma }_{\text{r}}}-{{\sigma }_{\text{ }\!\!\theta\!\!\text{ }}}}{r}=0$
联立（1）式和（2）式,引入边界条件 $r=r_{1}^{{}}$和 ${{\sigma }_{\text{r}}}=-{{p}_{1}}$,解得水泥环塑性区的应力分布表达式为：
$\left\{ \begin{align} & {{\sigma }_{\text{r}}}=-{{\left( \frac{{{r}_{1}}}{r} \right)}^{M}}\left( {{p}_{1}}+\frac{\alpha {{\sigma }_{\text{c}}}}{1-\alpha } \right)+\frac{\alpha }{1-\alpha }{{\sigma }_{\text{c}}} \\ & {{\sigma }_{\text{ }\!\!\theta\!\!\text{ }}}=-N{{\left( \frac{{{r}_{1}}}{r} \right)}^{M}}\left( {{p}_{1}}+\frac{\alpha {{\sigma }_{\text{c}}}}{1-\alpha } \right)+\frac{\alpha }{1-\alpha }{{\sigma }_{\text{c}}} \\ \end{align} \right.$
式中 $M=\frac{2+2b-2b\alpha -2\alpha }{2+2b-b\alpha }$ $N=\frac{2\alpha +b\alpha }{2+2b-b\alpha }$
由此可得塑性区水泥环外边界处的接触压力为：
${{p}_{\text{p}}}={{\left( \frac{{{r}_{1}}}{{{r}_{\text{p}}}} \right)}^{M}}\left( {{p}_{1}}+\frac{\alpha {{\sigma }_{\text{c}}}}{1-\alpha } \right)-\frac{\alpha }{1-\alpha }{{\sigma }_{\text{c}}}$
忽略塑性体积应变,根据体积弹性定律、几何方程,并联立平衡方程（（2）式）,通过积分可得水泥环塑性区的位移表达式为：
${{u}_{\text{cp}}}=\frac{\left( 1+{{\nu }_{\text{c}}} \right)\left( 1-2{{\nu }_{\text{c}}} \right)}{{{E}_{\text{c}}}}\left[ \frac{\alpha {{\sigma }_{\text{c}}}}{1-\alpha }r- \right.$$\left. \left( {{p}_{1}}+\frac{\alpha {{\sigma }_{\text{c}}}}{1-\alpha } \right)r_{1}^{M}{{r}^{N}} \right]+\frac{K}{r}$
对于水泥环弹性区、套管和地层的应力和位移可通过弹性力学厚壁圆筒理论中的拉梅公式和位移公式进行表征,如（6）式和（7）式所示：
$\left\{ \begin{align} & {{\sigma }_{\text{r}}}=\frac{R_{\text{i}}^{2}{{p}_{\text{in}}}-R_{\text{o}}^{2}{{p}_{\text{out}}}}{R_{\text{o}}^{2}-R_{\text{i}}^{\text{2}}}-\frac{R_{\text{i}}^{2}R_{\text{o}}^{2}\left( {{p}_{\text{in}}}-{{p}_{\text{out}}} \right)}{\left( R_{\text{o}}^{\text{2}}-R_{\text{i}}^{\text{2}} \right){{R}^{2}}} \\ & {{\sigma }_{\text{ }\!\!\theta\!\!\text{ }}}=\frac{R_{\text{i}}^{2}{{p}_{\text{in}}}-R_{\text{o}}^{2}{{p}_{\text{out}}}}{R_{\text{o}}^{2}-R_{\text{i}}^{\text{2}}}+\frac{R_{\text{i}}^{\text{2}}R_{\text{o}}^{\text{2}}\left( {{p}_{\text{in}}}-{{p}_{\text{out}}} \right)}{\left( R_{\text{o}}^{2}-R_{\text{i}}^{\text{2}} \right){{R}^{2}}} \\ \end{align} \right.$
$u=\frac{1-\nu }{E}\frac{\left( R_{\text{i}}^{2}{{p}_{\text{in}}}-R_{\text{o}}^{2}{{p}_{\text{out}}} \right)R}{R_{\text{o}}^{2}-R_{\text{i}}^{2}}+\frac{1+\nu }{E}\frac{R_{\text{i}}^{2}R_{\text{o}}^{2}\left( {{p}_{\text{in}}}-{{p}_{\text{out}}} \right)}{\left( R_{\text{o}}^{2}-R_{\text{i}}^{2} \right)R}$
同时,因弹性区水泥环内壁与塑性区水泥环外壁接触压力相等,则弹性区水泥环外壁接触压力可表示为：
${{p}_{\text{2}}}=\frac{\left[ \left( 1-\alpha +b-\alpha b \right)r_{\text{p}}^{2}+ \right.\left. \left( 1+\alpha +b \right)r_{2}^{2} \right]{{p}_{\text{p}}}}{r_{2}^{2}\left( 2+2b-\alpha b \right)}- \frac{\alpha \left( 1+b \right)\left( r_{2}^{2}-r_{\text{p}}^{2} \right){{\sigma }_{\text{c}}}}{r_{2}^{2}\left( 2+2b-\alpha b \right)}$
1.1.2 水泥环弹塑性模型的求解
以套管-水泥环-地层组合体内接触面处的位移相等为连续条件,并与（4）式和（8）式联立得到如下方程组：
$\left\{ \begin{align} & {{u}_{\text{so}}}={{u}_{\text{cpi}}} \\ & {{u}_{\text{cpo}}}={{u}_{\text{cei}}} \\ & {{u}_{\text{ceo}}}={{u}_{\text{fi}}} \\ & {{p}_{\text{p}}}={{\left( \frac{{{r}_{1}}}{{{r}_{\text{p}}}} \right)}^{M}}\left( {{p}_{1}}+\frac{\alpha {{\sigma }_{\text{c}}}}{1-\alpha } \right)-\frac{\alpha }{1-\alpha }{{\sigma }_{\text{c}}} \\ & {{p}_{\text{2}}}=\frac{\left[ \left( 1-\alpha +b-\alpha b \right)r_{\text{p}}^{2}+ \right.\left. \left( 1+\alpha +b \right)r_{2}^{2} \right]{{p}_{\text{p}}}}{r_{2}^{2}\left( 2+2b-\alpha b \right)}- \\ & \frac{\alpha \left( 1+b \right)\left( r_{2}^{2}-r_{\text{p}}^{2} \right){{\sigma }_{\text{c}}}}{r_{2}^{2}\left( 2+2b-\alpha b \right)} \\ \end{align} \right.$
以压裂时套管内压和地层压力增量为边界条件,即可求解组合体内任意位置的应力状态和位移。
1.2 水泥环界面裂缝应力场分析
1.2.1 界面裂缝应力场的表征
基于界面断裂力学,采用应力强度因子（SIF）法表征压裂工况下的水泥环界面裂缝应力场[13]：
${{K}_{1}}+\text{i}{{K}_{2}}=\frac{\underset{{r}'\to 0}{\mathop{\lim }}\,\left[ \sqrt{2\text{ }\!\!\pi\!\!\text{ }{r}'}\left( {{\sigma }_{\text{y}}}+\text{i}{{\tau }_{\text{xy}}} \right) \right]}{{{\left( {{r}'} \right)}^{\text{i}\varepsilon }}}$
其中：
$\varepsilon =\frac{1}{2}\ln \frac{\frac{3-4{{\nu }_{1}}}{{{\mu }_{1}}}+\frac{1}{{{\mu }_{2}}}}{\frac{3-4{{\nu }_{2}}}{{{\mu }_{2}}}+\frac{1}{{{\mu }_{1}}}}$
（11）式中下标1和2分别表示位于界面两侧的材料。
以水泥环-地层界面为例,界面裂缝应力场如图2 所示。可以发现,根据（10）式难以直接描述应力场内的多个载荷,因此,采用线性叠加法将界面裂缝应力场分解为受井筒径向应力和界面胶结强度影响的界面应力场、受压裂液流体载荷影响的压裂载荷场。
对于界面应力场,其数值上等于水泥环-地层界面初始应力、压裂导致的应力增量和界面胶结强度之和：
${{\sigma }_{\text{cf}}}\text{=}{{\sigma }_{\text{cf,i}}}+{{\sigma }_{\text{cf,p}}}+{{\sigma }_{\text{b}}}$
对于压裂载荷场,可将其分为平行于井筒方向和垂直于井筒方向的应力分量,其数值大小与压裂泵压、压裂液液柱压力和井筒摩阻相关。
综上,可采用（13）式分别表征界面应力场和压裂载荷场：
$\left\{ \begin{align} & {{\sigma }_{\text{cf}}}=\frac{{{K}_{\text{1, }\!\!\sigma\!\!\text{ }}}+\text{i}{{K}_{\text{2, }\!\!\sigma\!\!\text{ }}}}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }{r}'}}{{\left( \frac{{{r}'}}{2a} \right)}^{\text{i}\varepsilon }} \\ & {{\sigma }_{\text{y,p}}}+\text{i}{{\sigma }_{\text{x,p}}}=\frac{{{K}_{\text{1,p}}}+\text{i}{{K}_{\text{2,p}}}}{\sqrt{2\text{ }\!\!\pi\!\!\text{ }{r}'}}{{\left( \frac{{{r}'}}{2a} \right)}^{\text{i}\varepsilon }} \\ \end{align} \right.$
在分别求得界面应力场和压裂载荷场的应力强度因子后,界面裂缝应力场的应力强度因子可表征为：
$\left\{ \begin{align} & {{K}_{1}}={{K}_{\text{1,p}}}-{{K}_{\text{1, }\!\!\sigma\!\!\text{ }}} \\ & {{K}_{2}}={{K}_{\text{2,p}}}-{{K}_{\text{2, }\!\!\sigma\!\!\text{ }}} \\ \end{align} \right.$
1.2.2 界面裂缝扩展长度与方向评判
将界面裂缝应力场的应力强度因子与界面裂缝断裂的临界应力强度因子进行对比来评判界面裂缝是否会发生扩展[14]：
$K_{1,2}^{*}=\sqrt{{{\left( \frac{{{K}_{1}}}{1.0} \right)}^{2}}+{{\left( \frac{{{K}_{2}}}{1.6} \right)}^{2}}}\ge {{K}_{\text{IC,ini}}}$
界面裂缝受水泥环和地层力学性能及缝内压裂载荷指向的影响,还可能发生曲折扩展,导致水泥环或地层破坏并产生延伸裂缝。对此,采用最大周向应力准则评判裂缝是否发生曲折扩展及其曲折方向[15]：
$K_{_{,}}^{\text{*}}=\frac{\sqrt{K_{1}^{2}+K_{2}^{2}}}{2\cosh \left( \varepsilon \text{ }\!\!\pi\!\!\text{ } \right)}{{B}_{\text{j}}}\left( {{\theta }_{\text{o}}} \right)\ge {{K}_{\text{IJ,ini}}}$
2 井筒密封评判和水泥环力学性能设计方法
3 模型验证与实例分析
3.1 模型验证
为评价本文建立的弹塑性模型的准确性,对比不同屈服准则对计算结果的影响,采用与文献[6]研究中相同工况条件（55 MPa）开展计算和讨论。图5 展示了水泥环弹塑性半径和径向应力随套管内压变化规律。
由图5 a可见,水泥环弹塑性界面半径在套管内压达到一定值时随套管内压增加而逐渐扩展;以双剪统一强度理论为屈服准则进行计算时,水泥环将更早进入塑性状态。由图5 b可见,水泥环内外壁处的径向应力随套管内压降低而降低。假设界面胶结强度为2 MPa,当套管内压降至0时,基于Mohr-Coulomb准则计算得到的径向应力为正（0.89 MPa）,说明界面处为拉应力,但该应力小于界面胶结强度,水泥环不会发生界面剥离;而基于双剪统一强度理论计算得到的径向拉应力（2.58 MPa）大于胶结强度,说明水泥环存在产生界面微环隙的风险。
综上,基于不同屈服准则计算的水泥环弹塑性状态和应力变化规律相同,证明了模型的准确性;同时,双剪统一强度理论考虑了中间主应力影响,能够避免水泥环屈服及界面微环隙分析时偏保守的问题。
为分析压裂工况下水泥环界面密封性,Bunger等[17]设计了一套评价装置,将铝管和有机玻璃分别视为套管和模拟地层并在二者之间填充环氧树脂作为水泥环。通过在模拟水泥环一端预制3 mm裂缝并施加5 MPa套管内压和10 MPa流体载荷,测试了流体沿界面的窜流长度。装置尺寸和材料物理参数如表1 所示。
表1 Bunger等[17]研究中的装置、材料参数 |
| 材料 | 尺寸/mm | 弹性模量/GPa | 泊松比 |
|---|---|---|---|
| 套管（铝） | 14（内径） | 7.0 | 0.32 |
| 模拟水泥环（环氧树脂） | 17（内径） | 1.0 | 0.38 |
| 模拟地层（有机玻璃） | 20（内径） 21（外径） | 3.6 | 0.32 |
假设界面胶结强度为2 MPa,基于上述参数,采用本研究提出的界面裂缝应力场模型计算界面流体窜流长度,计算结果为165 mm,对比实测结果（175 mm）,二者误差约为5.7 %,证明模型计算结果准确。
3.2 实例分析
3.2.1 页岩油水平井概况
大港油田GD井为页岩油水平井,该井套管、水泥环和地层参数如表2 所示。其中水泥环屈服和抗拉强度分别为23.0,4.3 MPa。该井第2、3压裂段微地震事件重复程度较高,且其展布特征基本一致,说明压裂段间存在连通通道,为分析导致该现象的原因,开展下述井筒密封分析。
表2 套管、水泥环和地层参数 |
| 材料 | 弹性模量/GPa | 泊松比 | 内径/mm | 外径/mm |
|---|---|---|---|---|
| 套管 | 210 | 0.30 | 115.52 | 139.7 |
| 水泥环 | 8 | 0.17 | 139.70 | 215.9 |
| 地层 | 25 | 0.14 | 215.90 | 2 159.0 |
3.2.2 井筒密封分析
综上,GD井压裂时水泥环会发生塑性变形并存在微环隙产生风险;第2、3压裂段的水泥环-地层界面裂缝相互连通,是导致井筒密封失效的主要原因之一。
4 水泥环力学性能对井筒密封的影响
4.1 弹性模量、泊松比对水泥环屈服状态的影响
采用表2 所示参数,保持井筒尺寸、压裂参数及水泥环屈服强度恒定,计算不同水泥环弹性模量和泊松比条件下的水泥环内壁处三向应力,并代入（1）式中左式,将计算结果与右式（屈服强度）相减即可评判计算条件下的水泥环屈服状态：当数值等于0（图中虚线）,表示水泥环处于弹塑性的临界状态;小于0,表示水泥环未达到屈服的临界条件,仍为弹性;大于0,表示水泥环进入屈服状态。分析结果如图9 所示。
计算发现,降低水泥环弹性模量并提高其泊松比有利于避免水泥环屈服;当弹性模量、泊松比取值位于 $E-10.748\nu -4.947\le 0$区域（图中虚线下方区域）内时,水泥环恒为弹性状态。
4.2 弹性模量、泊松比对界面裂缝长度的影响
保持其他参数不变,改变水泥环弹性模量和泊松比,计算界面裂缝长度的变化规律,结果如图10 所示。
观察发现,当水泥环弹性模量保持恒定,泊松比增加对界面裂缝扩展长度呈非线性影响[9];泊松比一定时,水泥环弹性模量越大,界面裂缝扩展长度越短。当水泥环弹性模量和泊松比满足 $E-80{{\nu }^{2}}+45.333\nu -$ $13.333\ge 0$时（图中虚线上方区域）,界面裂缝扩展长度均小于8.7 m,此时即可保证界面裂缝不会与相邻压裂段连通。
4.3 弹性模量、泊松比对裂缝曲折扩展方向的影响
裂缝在沿界面扩展的同时还会有向界面两侧的水泥环或地层扩展的趋势[13]。由（16）式可知,裂缝的断裂角受双材料常数（ε）和界面裂缝应力场共同影响,在地层和压裂参数不变的条件下,水泥环弹性模量和泊松比是影响界面裂缝应力场应力强度因子和双材料常数的主要因素。当双材料常数为正、裂缝扩展角为负时,曲折裂缝会向材料2（地层）扩展;当双材料常数为负时,需重新对水泥环和地层参数进行假设,此时,若扩展角为负,裂缝就会曲折扩展进入水泥环。
4.4 弹性模量、泊松比对水泥环强度要求的影响
5 保障井筒密封的水泥环性能要求
针对不同失效形式,对水泥环力学性能的优化方向存在差异,只有水泥环力学性能指标能够兼顾其力学完整性和界面密封完整性才能保障井筒的有效密封。将避免水泥环屈服、界面密封失效和界面裂缝曲折扩展进入水泥环的力学性能要求区间绘制于同一图内,即可得到水泥环弹性模量、泊松比变化导致的井筒安全和风险区域（见图13 ）。
可以发现,风险区域可分为4种类型：①水泥环易发生屈服而产生塑性变形的风险区域;②界面裂缝易曲折扩展进入水泥环导致水泥环破坏的风险区域;③界面裂缝扩展过长,导致压裂段间互窜风险增加的风险区域;④存在压裂段间互窜和水泥环屈服风险的区域。而安全区域只有1种,为图中绿色范围,当水泥环弹性模量和泊松比取值居于该区域内时,水泥环不会发生完整性失效。同时,将安全区域中的弹性模量和泊松比分别对应于图12 中强度,即可得到保障井筒密封的水泥环强度要求,如图14 所示。
取图中峰值强度作为水泥环应当满足的屈服强度（24.62 MPa）和抗拉强度（3.30 MPa）要求,此时即可认为水泥环的强度、弹性模量和泊松比能够保障压裂工况下水泥环的完整性及井筒密封性。
6 结论
基于水泥环弹塑性模型和界面裂缝应力场模型,考虑水泥环本体拉伸破坏、塑性屈服、界面裂缝沿界面扩展和界面裂缝曲折扩展等多种失效形式,建立的井筒密封评判和水泥环力学性能设计方法经模型验证与实例检验证实计算精度较高。
根据水泥环力学性能设计方法构建的水泥环弹性模量、泊松比量化设计图版,明确了井筒安全和风险区域,量化了水泥环屈服强度和抗拉强度指标,更便于现场应用。
降低水泥环弹性模量、提高水泥环屈服强度和泊松比可避免水泥环发生塑性变形;提高水泥环抗拉强度可防止其拉伸破坏;提高水泥环弹性模量和泊松比对缩短界面裂缝扩展长度有利,但会增加界面裂缝曲折扩展进入水泥环的风险。
符号注释：
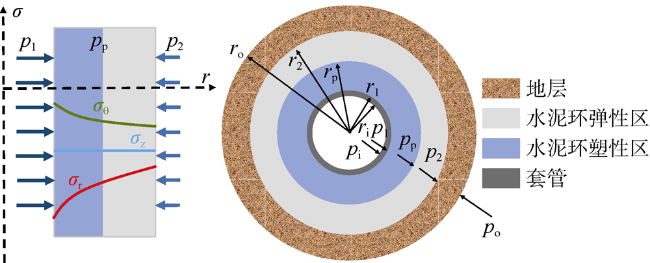
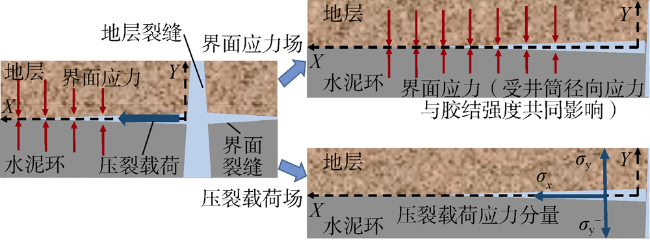
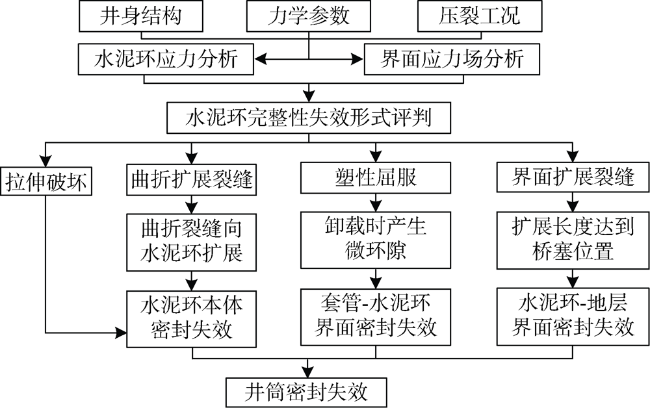
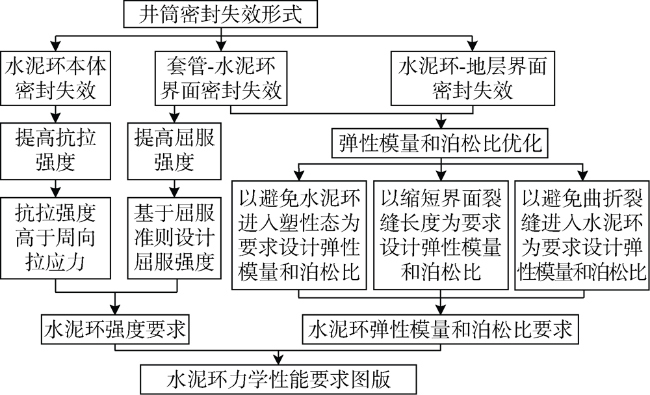
a——界面裂缝长度,m;b——反映中间主应力影响的权系数,无因次; ${{B}_{\text{j}}}\left( {{\theta }_{\text{o}}} \right)$——关于曲折裂缝断裂角的函数,无因次;Ec——水泥环弹性模量,Pa;E——弹性模量,Pa;i——虚数单位;K——积分常数,m2;K1,K2——界面裂缝的张开型和剪切型模态的应力强度因子,MPa·m1/2;K1,σ,K2,σ——受界面应力影响的界面裂缝张开型和剪切型模态的应力强度因子,MPa·m1/2;K1,p,K2,p——受压裂载荷影响的界面裂缝张开型和剪切型模态的应力强度因子,MPa·m1/2; $K_{1,2}^{*}$——界面裂缝的应力强度因子,MPa·m1/2;KIC,ini——判定界面裂缝扩展的临界应力强度因子,MPa·m1/2; $K_{,}^{*}$——界面裂缝向界面某侧曲折扩展时的应力强度因子,MPa·m1/2;KIJ,ini——判定裂缝曲折扩展的临界应力强度因子,MPa·m1/2;M,N——中间变量,无因次;p1——套管-水泥环接触压力,Pa;p2——水泥环-地层接触压力,Pa;pi——套管内压,Pa;pin——厚壁圆筒内壁压力,Pa;po——地层孔隙压力,Pa;pout——厚壁圆筒外壁压力,Pa;pp——水泥环弹塑性界面的接触压力,Pa;r——套管-水泥环-地层组合体某处的半径,m;r1——套管外壁（水泥环内壁）半径,m;r2——水泥环外壁（地层内壁）半径,m;ri——套管内壁的半径,m;ro——地层外壁的半径,m;rp——水泥环弹塑性区界面半径,m;R——厚壁圆筒内任一点半径,m;Ri——厚壁圆筒内半径,m;Ro——厚壁圆筒外半径,m; ${r}'$——表征界面裂缝指向的极坐标半径;u——位移,m;ucei——水泥环弹性区内壁位移,m;uceo——水泥环弹性区外壁位移,m;ucp——水泥环塑性区任意位置的位移,m;ucpi——水泥环塑性区内壁位移,m;ucpo——水泥环塑性区外壁位移,m;ufi——地层内壁位移,m;uso——套管外壁位移,m;X——井筒轴向坐标轴,m;Y——井筒垂向坐标轴,m;α——拉压强度比,无因次;ε——双材料常数,无因次;θ0——曲折裂缝的断裂角度,（°）;ν——泊松比,无因次;ν1,ν2——材料1和2的泊松比,无因次;νc——水泥环泊松比,无因次;σ——应力,Pa;σb——胶结强度,Pa;σc——水泥环屈服强度,Pa;σcf——水泥环-地层界面应力,Pa;σcf,i——水泥环-地层界面初始应力,Pa;σcf,p——受井筒内压导致的界面应力增量,Pa;σr——径向应力,Pa;σx——平行于井筒方向的压裂液流体载荷,Pa;σx,p——压裂载荷在平行于界面方向上的应力,Pa;σy——垂直于界面的应力,Pa; $\sigma _{\text{y}}^{+}$, $\sigma _{\text{y}}^{-}$——压裂载荷在指向地层和井筒方向上的应力,Pa;σy,p——压裂载荷在垂直于界面方向上的应力,Pa;σz——轴向应力,Pa;σθ——周向应力,Pa;μ1,μ2——材料1和2的剪切模量,Pa;τxy——平行于界面的应力,Pa。