0 引言
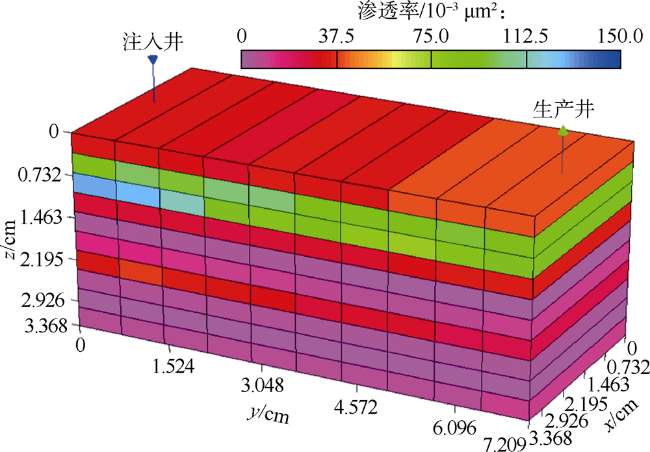
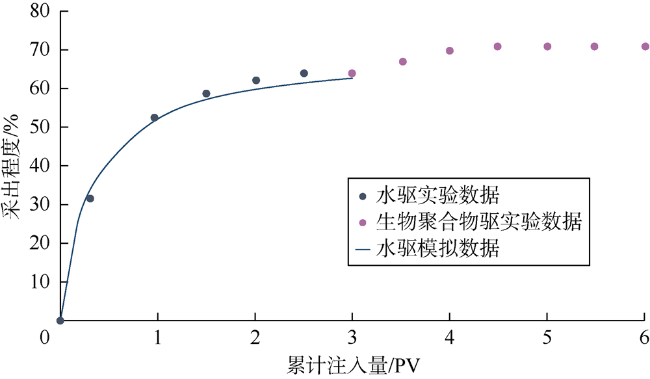
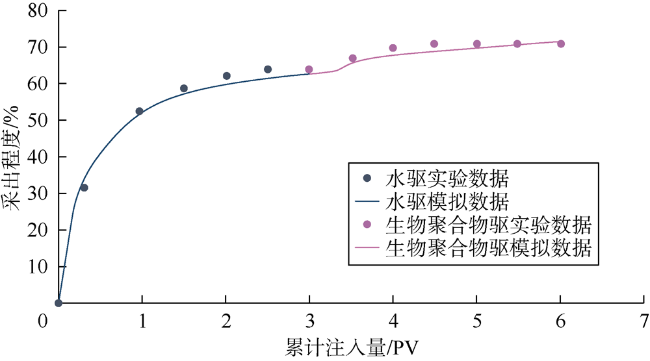
1 数值模型与数据
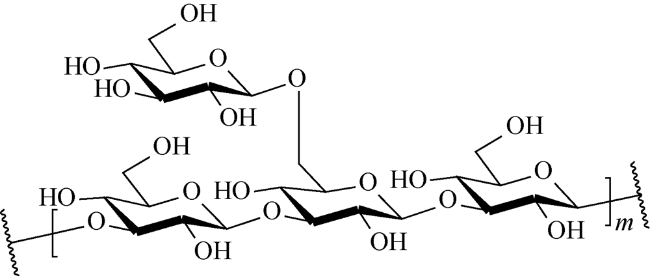
2 生物聚合物特性模拟
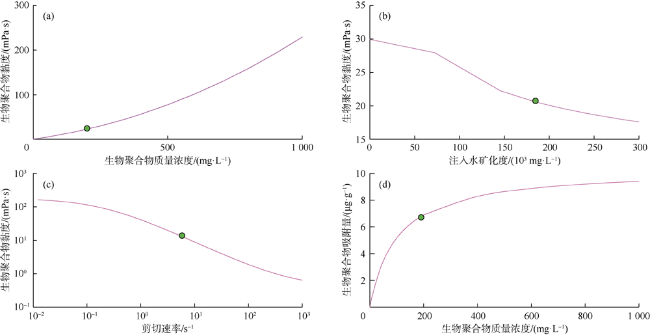
2.1 生物聚合物黏度
2.2 剪切效应
2.3 生物聚合物吸附量
2.4 渗透率降低系数
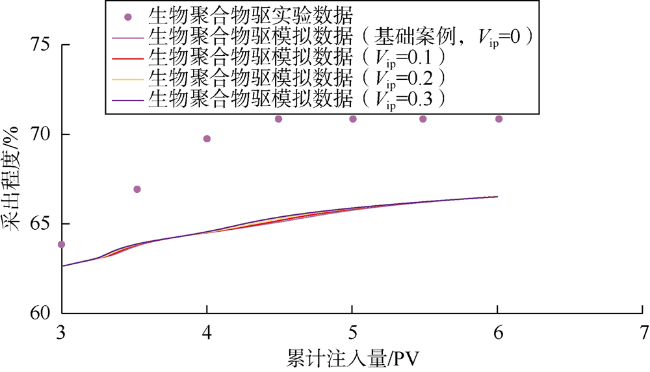
2.5 不可及孔隙体积
2.6 捕集数
3 数值模拟结果与讨论
表2 生物聚合物驱三次采油的敏感性分析参数 |
| 变量 | UTCHEM 输入参数 | 设定值 |
|---|---|---|
| 不可及孔隙体积 | Vap | 0.7, 0.8, 0.9, 1.0* |
| 生物聚合物吸附量 | ap1 | 0, 1.857*, 5.380, 53.800 |
| 渗透率降低系数 | cKr | 0, 0.008 83*, 0.011 00, 0.013 00 m |
| 剪切速率系数 | ${{\dot{\gamma }}_{c}}$ | 0, 3.97, 10.12*, 19.85, 39.70 |
| 注入水硬度 | βp | 1*, 10, 20, 40 |
注:“*”指基础案例中使用的值 |
3.1 不可及孔隙体积
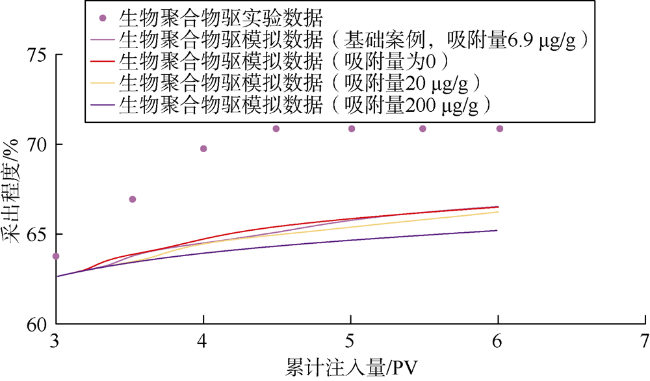
3.2 生物聚合物吸附量
表4 生物聚合物吸附量的敏感性分析结果 |
| 生物聚合物吸附 量/(µg·g-1) | 输入参数 ap1 | 相对水驱提高采收率幅度/百分点 | 与基础案例采收率差异/百分点 |
|---|---|---|---|
| 6.9 | 1.857 | 3.90 | |
| 0 | 0 | 3.93 | 0.03 |
| 20.0 | 5.380 | 3.60 | -0.30 |
| 200.0 | 53.800 | 2.57 | -1.33 |
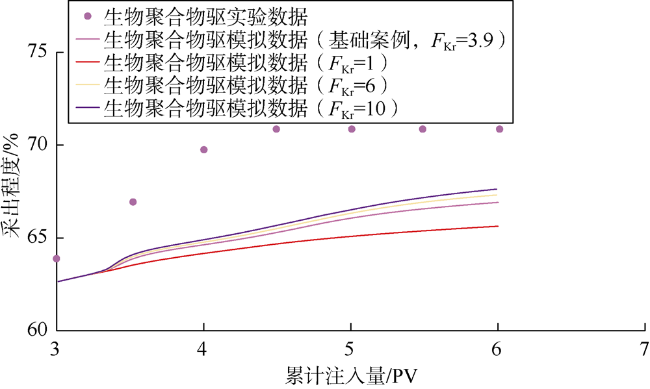
3.3 渗透率降低系数
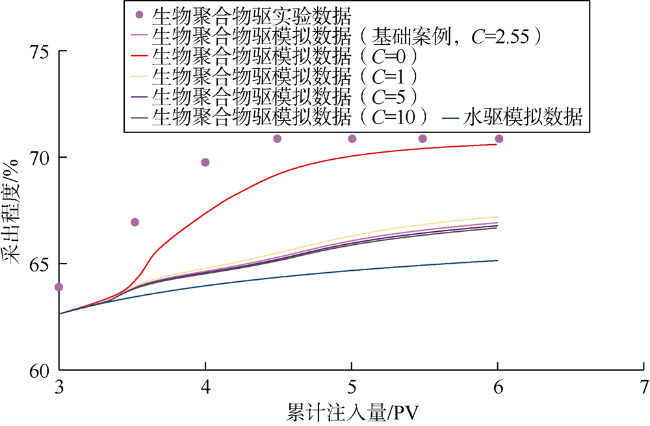
3.4 剪切速率系数
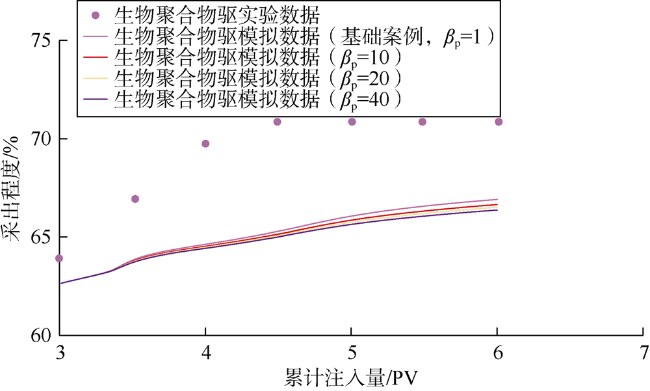
3.5 注入水的硬度
表7 注入水硬度的敏感性分析结果 |
| βp | 相对水驱提高采收率 幅度/百分点 | 与基础案例采收率 差异/百分点 |
|---|---|---|
| 1 | 3.90 | |
| 10 | 3.89 | -0.01 |
| 20 | 3.80 | -0.10 |
| 40 | 3.74 | -0.16 |
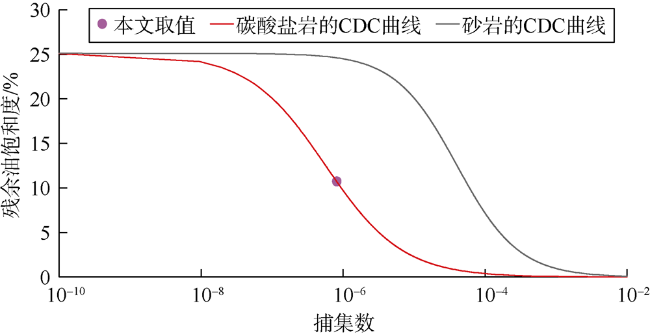
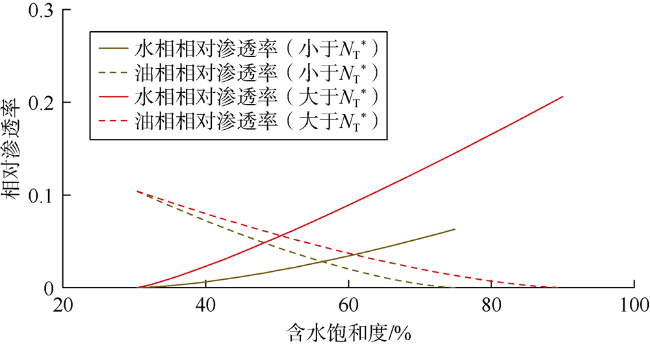
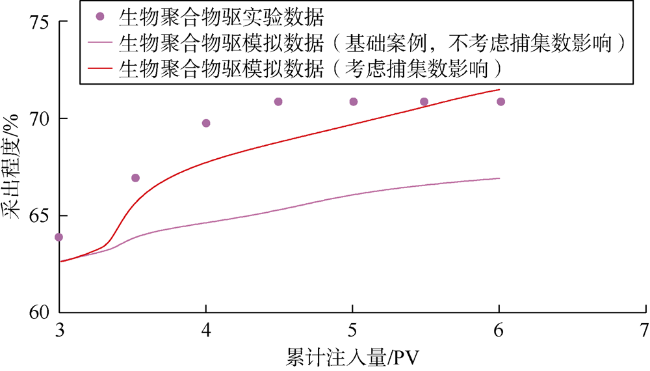
3.6 捕集数
表8 水驱和生物聚合物驱阶段的捕集数 |
| 注入 阶段 | 达西流 动速度/ (m·d-1) | 120 ℃下 水相黏度/ (mPa·s) | 界面张力/ (mN·cm-1) | 捕集数 | 残余油 饱和度/ % |
|---|---|---|---|---|---|
| 水驱 | 0.254 | 0.385 | 30 | 3.77×10-8 | 25.1 |
| 生物聚合物驱 | 0.254 | 10.000 | 30 | 9.80×10-7 | 10.0 |