第一作者简介:ELYAS Hedayati Rad(1993-),男,伊朗人,现为伊斯兰阿扎德大学科学和技术学院石油工程系在读博士研究生,主要从事石油勘探工程方面研究。地址:Department of Petroleum Engineering, Science and Research Branch, Islamic Azad University, Tehran, Iran,邮政编码:15847-43311。E-mail: e. hedayatirad@yahoo.com
地质分层是石油工程中的一项重要的基础工作。叠后地震数据和测井数据的时间序列能反映地下分层。由于地层的非均质性和不同成因特性,它们表现出具有复杂模式的多重分形特性。在多重分形结构中,序列中的任何部分都具有不同的赫斯特(Hurst)指数,可反映其性质,并可用于分区检测。时间序列是井眼附近的叠后地震道和测井数据。自相似自回归外生(SAE)模型是一种改进的方法,它可以将自相似的叠后地震和测井段置于具有相同岩性的地层之间,这样就可以通过SAE模型对地震数据进行分层识别。
Layering detection is an important step in petroleum engineering. Time series of post-stack seismic data and wire-line log data belong to subsurface layering. They exhibit multifractal properties with complex patterns because of the heterogeneity and different genetic properties in the earth layers. In a multifractal configuration, any piece of a series has a distinct Hurst exponent that reflects its nature and can be used for zone detection. Time series are post-stack seismic traces and wire-line log data near the well-bores. Self-similar Autoregressive Exogenous (SAE) model is a modified method which can place self-similar post-stack seismic and wire-line log segments across layers with the same lithology. The results satisfy the capability of layering identification from seismic data by SAE model.
在石油工程中, 通常将露头、地震、测井、岩心及生产数据资料用于储集层评价[1], 可以从以下3种类型的数据中提取和确定储集层的深度和厚度:①具有低垂向分辨率和高横向分辨率的地震数据; ②具有中等的横向分辨率和高垂向分辨率的测井数据; ③具有非常高的垂向分辨率、但没有横向信息的岩心数据。近年来, 通过测井资料进行分形分段和分层检测取得了很好的应用效果, 发展前景很好[2]。地震数据的分形特性以及利用其特征进行分层很关键, 难度也较大, 因为这类数据具有较大的覆盖范围。此外, 当只有地震数据可用时, 通过其他资料提取的地层信息非常关键。
自相似性下的分形概念由Mandelbrot于1967年提出, 并于1968年与Van Ness一起扩展到时间序列[3]。分形布朗运动(fBm)和分形高斯噪声(fGn)是自相似时间序列的经典形式[3, 4, 5]。可以通过定义的赫斯特(Hurst)指数或霍尔德(Hö lder)正则度(H)(由哈罗德· 赫斯特于1951年提出)来创建随机游走或布朗游走[6]。当H值为0.5~1.0, 则游走将显示长期记忆; 如果它们是相关且持久的, 称为fBm或fGn[3, 7]。它可以描述许多自然现象, 例如物理学、地球物理学和地质学[8, 9, 10, 11, 12]现象。当H值为0~0.5, 则游走是不持久且负相关的。当H=0.5, 则游走是随机的[13]。可以通过多种方法对H进行分析, 例如重标极差法、小波变换、半方差图分析、功率谱、功率谱密度、去趋势波动分析和粗糙长度法[14]。
单分形或同质分形用于具有恒定赫尔德指数和单一fBm的信号。Mandelbrot针对湍流现象首先提出了多重分形[15], 后来被用于许多领域[16, 17, 18]。分形维在许多研究中被广泛应用, 例如:比较股票市场的数据[19]、石油测井数据中分形特性的变化[20]、地层的岩石物性分段[2]、通过测井数据的分形特性进行岩相识别[21]和天然地震数据的分形分析[22]。从沉积环境中提取属性的垂直序列显示出具有长记忆相关性的分形性, 并且具有类似于fGn(H=0.7)的特征[20]。在具有多重分形结构的系统(例如股票市场或地层)中, 系统的任何部分都可由不同的H[19, 23, 24]来区分。在地质学中, 可以通过不同的分形特性来揭示其非均质性[25]。每个H值代表一个单独的层, 属于特定的沉积环境, 并用于分析局部的时间序列、聚类和检测床层[2, 26, 27]。根据这些研究, 可以推测自相似性存在于地层的各个尺度上。由于岩石形成过程中的沉积、成岩作用和岩化作用差异, 在地震及测井数据上具有多重分形特征[24, 28]。
数据分段用于查找时间序列分段、检测故障点以及查找系统的不同模式, 它是通过诸如最大似然、主成分、判别函数分析和数据聚类之类的方法完成的。这些方法需要大量数据, 但有时无法获取大量数据, 因此具有局限性[29]。在本研究中, 考虑了各尺度的沉积岩的分形特性, 通过多分形去趋势波动分析(MF-DFA)在地震数据的地震道上对多分形性进行研究。通过多重分形所得到的结果, 使用小波变换法测量这些地震道随深度变化的分形维, 然后通过自回归外生(AE)模型将它们聚类为等效层。这种方法为地震解释提供了一种新的数学方法。
本研究着重地震数据的多重分形及通过自相似AE(SAE)模型进行的分形分段, 即通过对地震数据进行MF-DFA分析, 确定多重分形的类型。找到多重分形的来源之后, 应用分形分段, 将固定或单分形的块或特定层与其他部分分开。笔者使用测井和叠后地震数据进行分析。
地震属性资料可以对油藏属性和地层岩性进行定量和定性解释。地震属性基本上可分为两类:物理属性和几何属性。物理属性与地震波传播、岩性和其他相关属性有关, 包括表示地震数据连续性的瞬时属性和表示小波及其振幅谱特征的小波属性。几何属性包括倾角、方位角和不连续性属性, 它们取决于地震数据在X、Y和Z方向上的振幅变化[30]。利用地震数据的分形特性是一种新颖的想法, 几十年来人们一直在使用这种方法[31, 32, 33, 34]。在所有地震属性中, 功率谱密度或功率谱是与分形几何形状最相关的地震属性, 并且与下一节中描述的赫斯特指数有关。总之, 利用这种关系和统计AE模型来检测地层是本文的创新。
为了找到序列的结构, 笔者分析了数据的标度指数, 它显示出任意尺度上的结构, 都可以用于对数据进行解释和分类。通常情况下, 对N个时间步长为τ 的简单随机游走引入具有随机运动的时间序列x(t), 公式表示如下:
$\left\{ \begin{align} & X(t)=\sum\limits_{i=1}^{N}{{{\xi }_{i}}} \\ & X(t)-X(t-\tau )={{\xi }_{N}} \\ \end{align} \right.$ (1)
其中, X(t)是时间t=Nτ 时的总旅行距离。
时间序列的自相关表示如下:
${{R}_{XX}}(k)=\left\langle {{X}_{i}}{{X}_{i+k}} \right\rangle =\frac{1}{2\text{ }\!\!\pi\!\!\text{ }}\int\limits_{0}^{2\text{ }\!\!\pi\!\!\text{ }}{S(\omega )\cos (k\omega )\text{d}\omega }$ (2)
(2)式中< > 是对一个时间段求平均值。(2)式是功率谱的逆余弦傅立叶变换, 因此, 一个序列的功率谱是其自相关函数的傅立叶变换。
fGn是一个信号或一个随机变量, 其标度可以用功率谱密度定义为:
$f(at)\equiv {{a}^{H}}f(t)\ \ \ \ (a> 0)$ (3)
(3)式中“ ≡ ” 是分布均匀性, H为赫斯特指数, 表示过程的长期依赖程度, 0< H< 1。
当H=0.5时, 表示信号是白噪声或随机噪声, 并且遵循fBm规律。对于白噪声, 自相关会随时间衰减, 并且其平均值与时间步长(τ )存在如下关系:
${{R}_{XX}}(\tau )\propto {{\tau }^{2H-2}}\ \ \ \ (H=0.5)$ (4)
当0< H< 0.5时, 表示信号为非持续性, 随机游走会在任何一步之后改变其方向。对于此赫斯特指数范围, 功率谱集具有自相关, 表示如下:
$\left\{ {{R}_{XX}}(\tau ) \right\}=\left\{ {{\tau }^{-1}}, {{\tau }^{-1.25}}, {{\tau }^{-1.5}}, {{\tau }^{-1.75}}, {{\tau }^{-2}} \right\}$ (5)
该信号具有短时记忆, 并且该过程以单调和双曲线形式快速衰减为零。
当0.5< H< 1.0时, 表示信号具有持续性, 这意味着随机游走会继续进行并逐步向其游走方向持续。此运动的功率谱具有其自身的特定自相关函数, 表示如下:
$\left\{ {{R}_{XX}}(\tau ) \right\}=\left\{ {{\tau }^{-1}}, {{\tau }^{-0.75}}, {{\tau }^{-0.5}}, {{\tau }^{-0.25}}, {{\tau }^{-0}} \right\}$ (6)
(6)式为长尾记忆, 表明自相关函数会随时间缓慢衰减[13]。
具有单个标度指数的简单单分形样式不会显示出所有的现象。MF-DFA是一种分析多重分形源的程序, 与去趋势波动分析(DFA)相比, 它的编程算法简单得多。DFA和MF-DFA均可用于确定非平稳噪声时间序列中的分形标度特性和远距离相关性[35, 36, 37], 它们被广泛应用于DNA序列、心率动态、长期气象记录[38, 39, 40]以及地质学、生物学、物理学、经济学和音乐等领域[4, 41, 42]。
确定一个有限序列的多重分形。假设时间序列$\left\{ p(i) \right\}\begin{matrix} , & i=1, 2, \cdots , N \\\end{matrix}$, N是序列的长度或者是构成该序列的振幅数。MF-DFA程序的应用如下[43, 44]:
①构建剖面$\left\{ p(i) \right\}\begin{matrix} , & i=1, 2, \cdots , N \\\end{matrix}$, $\bar{p}=\frac{1}{N}\sum\nolimits_{j=1}^{N}{p(j)}$。
②将剖面P(i)等分成${{N}_{l}}\equiv \operatorname{int}(N/l)$段。为避免遗漏该序列的短端部分, 从该序列的末尾重复相同的过程。因此, 需对2Nl段(υ )作进一步分析。
③进行最小二乘拟合并将其从原始剖面中去除, 从而对2Nl段进行趋势计算。然后, 在每个段中计算去趋势剖面的方差, 公式如下:
${{F}^{2}}(l, \upsilon )=\frac{1}{l}\sum\limits_{i=1}^{l}{{{\left\{ P[(\upsilon -1)l+i]-{{P}^{\upsilon }}(i) \right\}}^{2}}}\ (\upsilon =1, 2, \cdots , {{N}_{l}})$ (7)
$\begin{align} & {{F}^{2}}(l, \upsilon )=\frac{1}{l}\sum\limits_{i=1}^{l}{{{\left\{ P[N-(\upsilon -{{N}_{l}})l+i]-{{P}^{\upsilon }}(i) \right\}}^{2}}} \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\upsilon ={{N}_{l}}+1, {{N}_{l}}+2, \cdots , 2{{N}_{l}}) \\ \end{align}$(8)
④对所有段的方差求平均值, 局部波动如下:
$\left\{ \begin{align} & {{F}_{q}}(l)={{\left\{ \frac{1}{2{{N}_{l}}}\sum\limits_{\upsilon =1}^{2{{N}_{l}}}{{{\left[ F_{{}}^{\text{2}}(l, \upsilon ) \right]}^{q/2}}} \right\}}^{1/q}}\ \ \ \ \ \ \ \ \ \ q\ne 0 \\ & {{F}_{0}}(l)=\exp \left\{ \frac{1}{4{{N}_{s}}}\sum\limits_{\upsilon =1}^{2{{N}_{l}}}{\ln {{\left[ F_{{}}^{\text{2}}(l, \upsilon ) \right]}^{q/2}}} \right\}\ \ \ \ q=\text{0} \\ \end{align} \right.$ (9)
其中q是局部波动的阶数, q为正值时会放大波动很大的片段, 而q为负值时会放大波动很小的片段, q=0是中性中点, 显示两种波动的影响。对于l和q的不同值, 重复上述步骤。
⑤Fq(l)随l变化的关系式如下:
${{F}_{q}}(l)\approx {{l}^{h(q)}}$ (10)
为实现统计一般性, 笔者排除了l< 10及l> N/4的情况, 因为该范围的数量很少并且第4步的平均过程不可靠[44]。h(q)是广义的赫斯特指数, 等于lnFq(l)和lnl的最小二乘拟合斜率。不同的q显示波动函数的标度特性。可以从h|q=2获得赫斯特指数H。对于不同的q, 如果h(q)恒定不变, 则时间序列是单分形的。否则, 如果h(q)发生变化, 则时间序列是多重分形的。当q> 0时, h(q)显示波动较大段的标度特性; 当q< 0时, h(q)显示波动较小段的标度特性[13]。
多重分形的原因通常是由于存在广泛的密度函数, 该函数在随机序列(时间序列的非高斯概率密度函数(PDF))中存在肥尾现象或长期相关性(波动幅度较小和较大的远程时间相关性)或两者兼而有之。通过分析原始、替代(相位随机化)和叠加时间序列中的多重分形来区分不同类型的多重分形特征[44, 45]。
在序列PDF中出现肥尾时, 叠加不能消除多重分形, 并且如果多重分形仅属于长记忆相关性, 则叠加将消除多重分形源并破坏所有相关性[44], 因此会发现hshuffle(q)=0.5。
如果在大、小尺度下波动具有不同的相关性(PDF肥尾), 类似于高斯分布, 替代序列会破坏多重分形的来源。另一方面, 通过替代时间序列, 该序列的离散傅立叶变换系数的相位被[0, π ]的一组均匀量所代替, 而且PDF变为高斯分布。同时, 替代序列中的相关性不变。
如果同时存在两种类型的多重分形, 则替换和叠加序列的一般赫斯特指数均取决于q, 并且它们的多重分形值均低于原始序列[43]。
叠加会对时间序列值的阶数随机化, 这样, 时间序列的PDF不会因叠加而改变, 但会破坏空间相关性[45]。Theiler等人在1992年提出了时间序列的替代或相位随机化方法[46]。通过该相位随机化, 可以评估PDF广度[47]。为了以随机方式计算具有相同均值、方差和功率谱的替代时间序列, 可以使用以下过程[47, 48]。首先, 将该序列转换为复杂的数组, 然后进行离散傅里叶变换。在(0, π )形成随机相位之后, 将随机化的相位插入傅立叶变换数据中, 最后应用傅立叶变换反演将数据转换为原始状态。
某一频段的时间序列和地震记录具有混沌性质[49]。SAE方法涉及两个常规自回归和非线性赫斯特指数地震属性的组合[50]。自回归模型用于不同情况, 例如民用建筑中的损伤检测和不同现象的离散时间动力系统分析[51, 52]。在不同的H值估计方法中, 选择小波变换方法是因为它可以计算任何序列中的H值[53]。当常规的频率域和时间域分析无法提供有价值的结果时, 赫斯特指数作为一种属性, 它是一种了解非平稳信号的有效参数。它给出了与分形维数直接相关的特定时间和频率信息, 用于量化时间序列中点的相关性, 尤其是根据点的可预测性和混乱程度对其进行分类[53, 54, 55]。
将一个序列的分形分段描述为将其分割成固定的小块。本研究旨在将SAE模型应用于地震数据以检测小层。为此, 在检测并证明了地震数据的多重分形性之后, 通过以下方法进行SAE模型分段:①应用最佳和最小长度相关的方法进行H估计; ②为H估计选择最佳分段长度; ③在H序列上执行AE模型分段; ④使用最优方差控制分段的真实水平。
首先, 使用小波变换方法估计H。然后, 选择最佳间隔并将其应用于合成和实际地震时间序列的H值估计。之后, 在H序列中应用AE模型分段。AE模型分段是根据Ljung[56]开发的基于卡尔曼(Kalman)滤波技术的多个并行模型进行的。通过估计线性回归模型[57], 此过程是系统识别中最基础的工作。因此, 系统参数仅在特定时间实例处发生变化, 并且是分段不变的。具体参考Basseville、Gustafsson和Balakrishnan等的研究[58, 59, 60]。
AE算法如下:考虑一个涉及u(k)和y(k)两种信号的系统。AE模型具有自回归部分A(q, θ )y(k)和外生变量B(q, θ )u(k), 可用以下关系式表示:
$\left\{ \begin{align} & A(q, \theta )y(k)=B(q, \theta )u(k)+e(k) \\ & A(q)=1+{{a}_{1}}{{q}^{-1}}+{{a}_{2}}{{q}^{-2}}+\cdots +{{a}_{{{n}_{a}}}}{{q}^{-{{n}_{a}}}} \\ & B(q)={{b}_{1}}{{q}^{-1}}+{{b}_{2}}{{q}^{-2}}+\cdots +{{b}_{{{n}_{b}}}}{{q}^{-{{n}_{b}}}} \\ \end{align} \right.$ (11)
其中, e(k)是非平稳白噪声, 并且参数向量θ 定义为:
$\theta ={{[\begin{matrix} {{a}_{1}} & {{a}_{2}} & \cdots & {{a}_{{{n}_{a}}}} \\\end{matrix}\begin{matrix} {{b}_{1}} & {{b}_{2}} & \cdots & {{b}_{{{n}_{b}}}} \\\end{matrix}]}^{T}}$
如果$\varphi (k)=[\begin{matrix} -y(k-1)\ \ -y(k-2)\ \ \cdots \ \ -y(k-{{n}_{a}}) & u(k-1)\ \\\end{matrix}$ $u(k-2)\ \ \cdots \ \ u(k-{{n}_{b}}){{]}^{T}}$, 则回归向量φ (k)与参数向量θ 的关系如下:
$\hat{y}(k, \theta )={{\theta }^{T}}\varphi (k)={{\varphi }^{T}}(k)\theta $ (12)
该方程是线性回归, 可以通过最小二乘法[61]估计参数向量θ 。
本研究所用数据为伊朗西南部波斯湾的叠后地震数据及3口井的常规测井数据, 地层岩性主要为白云岩、灰岩、泥灰岩、砂岩和页岩, 厚度约为10 000 m。这些沉积物来自中生代到第四纪的新特提斯洋, 也被称为扎格罗斯褶皱带, 宽120~250 km, 长1 375 km[62]。由于地层的非均质性及其地球物理特征差异, 不同层位具有不同的分形特征[63]。研究区的地质柱状剖面与其他地区类似, 由蒸发岩、砂质灰岩、泥质灰岩和白云岩构成。储集层岩性为碳酸盐岩。
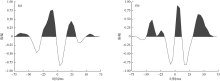
当能量从炸药爆炸中释放出来或由可控震源车产生时, 基于地层的速度和密度, 将一个脉冲或一系列脉冲发送到地层所在深度并反射到达地层顶部之后, 通常会发生反射、折射和透射。反射波的幅度和强度取决于两层之间的声阻抗的差值或反射系数。这些脉冲在穿过具有不同反射率的地层时发生变化, 然后被远离脉冲源的地震检波器记录下来。这是子波与地层反射系数的褶积。在本研究中, 为了制作合成地震道, 笔者使用了从地震数据中提取的子波(见图1), 并且根据测井数据计算出了波阻抗。
在正演模拟时, 子波在确定地震数据的振幅、相位和频率方面至关重要, 本研究中所使用的子波具有适当振幅和相位, 源自实际测井和地震数据[64, 65]。振幅谱完全是根据地震数据统计得出, 相位谱是从测井数据中提取的。以这种方式提取地震子波, 以确保了井眼合成地震道可以很好地代表井旁地震道, 并且深度与地震剖面深度完全匹配。
原始、替代和叠加数据的MF-DFA将阐明多重分形的类型和来源。图2显示了原始序列、替代序列和叠加序列中H对q的依赖性。当H> 0.5时, 它显示出正相关和持续时间序列。地震道的多分形性来源既有长记忆相关性, 又有PDF广度。叠加序列和原始序列之间的赫斯特指数差值大于替代序列和原始序列之间的赫斯特指数差值。因此, 相关性引起的多重分形性强于肥尾引起的多重分形性。这是由于地层的两个物理特性造成的:沉积环境增强了相关性, 而非均质性则导致了PDF广度, 两者均由地震数据所记录。MF-DFA证明这些数据中存在多重分形, 并且每一个地层都有代表其分形特征的特定H值。
在SAE模型分段中, 研究的间隔和e(t)的方差很重要。赫斯特指数估计对时间序列的分段长度敏感, 并且分段水平受e(t)的方差影响, 两者都是通过反复试验来检查和选择的。因此, 在运行最终模型之前, 首先要对模型进行测试以确定评估赫斯特指数的最佳时间间隔。通过几种方法在不同的时间间隔内估算赫斯特指数, 并通过比较得出相同的结果。其次, 在对段的长度初始化之后, 方差取决于模型在时间间隔内找到的分区数。地震道的理想分段间隔为80 ms, 较小的间隔值会增加赫斯特指数估计的误差, 而较大的间隔值会降低分段的分辨率。选择0.02 ms作为e(t)方差的最佳值, 值越大, 分区数越小, 反之亦然。
2.2.1 理论楔形模型分析
研究表明, 在不同标度下岩石的分形特性与其特性之间存在相关性, 它们是良好的分形体, 其分形特性与其标度无关。这些特征包括岩石类型、总有机质含量、在对流和扩散过程中酸性和活性流体含量、润湿性、颗粒大小、总孔隙体积、孔隙结构、颗粒间和颗粒内孔隙体积大小、比表面积、黏土矿物含量、渗透性等。这些研究的结果表明, 估计的H值取决于许多因素。页岩H值的范围为0~1, 灰岩H值的范围为0.25~0.65[66, 67, 68, 69, 70, 71, 72, 73]。为进行合成楔形建模, 笔者分析了页岩和灰岩这两种岩石类型, 并将灰岩的H平均值定为0.45, 将页岩的H平均值定为0.70。
楔形建模用于了解地震数据处理的垂直分辨率。调谐使两个反射信号要么显示为一个信号, 要么显示为无信号。因此, 该厚度表示子波可以识别的最小地层分辨率。在当前的楔形建模中, 将雷克子波与地层反射系数进行褶积, 以分析SAE模型的最小分辨率。地震数据的平均频率为25 Hz。因此, 使用25 Hz频率的雷克子波对20度楔形模型进行2D零偏移测量。地表均为泥岩, 密度为2.3 g/cm3, 声波速度为3 000 m/s; 楔形体为灰岩, 密度为2.6 g/cm3, 声波速度为5 000 m/s。楔形模型的合成地震数据有2 000道, 记录的采样率为1 ms, 道间距为1 m。
楔形模型的反射率剖面如图3a所示。SAE方法利用地面的分形特性对地层进行检测和分类, 因此, 类似于实际数据, 在泥页岩地区, 认为H值为0.7的fBm的小反射构成了页岩介质; 在灰岩楔形体中, H值为0.45的fBm的小反射为灰岩介质。两个区域边界处的反射系数为± 0.3, 这取决于这两个区域的声波阻抗差。
该楔形模型的最终2D零偏移剖面如图3b, 针对不同地震道的SAE分段如图3c所示。可以看出, 当楔形体的时间厚度小于100 ms(薄层)时, 该模型只能检测到第1个界面, CDP(共反射点道集)为500; 当时间厚度大于100 ms时, 两个界面都可以很好地检测到(CDP为1 500和2 000); 当厚度为100 ms左右时, 可以很好地检测到第1个界面, 但在检测第2个界面时出错(CDP为1 000)。
2.2.2 实际数据分析
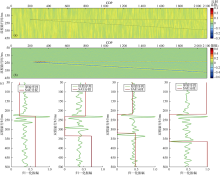
声波阻抗上的SAE模型分段结果, A、B和C井的合成地震道以及井旁地震道上SAE模型分段结果如图4、图5和图6所示。为了更好地进行曲线对比, 所有x轴数据都在最小值和最大值之间进行了归一化处理。
由于A井有部分声波阻抗数据缺失, 故本次对B井和C井使用声波阻抗、合成地震道和实际地震道进行地质分层。在B井中, 可以通过声波阻抗和合成地震道很好地识别所有小层的顶部; 使用地震道数据成功识别出6个小层的顶部, 但在识别F5和F10小层时略有偏移, 未能识别出F2、F4和F9小层顶部。对于C井中的8个小层的顶部, 其中6个可以通过各种数据很好地识别, 唯F1小层的顶部不能通过声波阻抗来识别, 但F7小层的顶部只能通过声波阻抗来识别。总体而言, 与测井数据相比, 地层厚度小、地震道质量差是导致使用SAE方法地层识别时出现误差的两个主要原因。
尽管实验地震数据的质量较差(最小分辨率约为10 m), 但仍能很好地识别具有特定分形特性的地层, 测井数据的分辨率为几厘米。识别结果是地层的边界, 与岩性变化相对应, 并不总是等于地层顶部。分段间隔大小是降低结果分辨率的另一个因素, 因为某些点为新的分形点, 并且SAE模型的结果显示出较小的上移和下移。
对测井、合成地震数据和实际地震数据的声波阻抗进行的自相似分段与地层顶部结果对比发现, 在某些情况下, 地震数据的自相似分段在检测地层顶部时更为准确。这项研究的结果与Shiri等人在2012年研究的测井数据的SAE模型分段相当[2]。
MF-DFA是研究确定信号(如地震数据)的多重分形特性的有用方法, 通过比较原始、叠加和替代的地震道, 发现多重分形的原因更多是与长期相关性有关, 而不是PDF广度。此外, 影响长期相关性和PDF广度的主要因素是沉积环境和非均质性。本文提出的SAE模型分段是对叠后地震数据和测井数据进行的, 研究结果表明, 地震数据和测井数据的SAE模型分段可以检测垂向上岩性的突变和渐变。基于地层的固有分形特性(反映在地震和测井数据上)的SAE模型分段是识别地层岩石物性变化的有效工具, 当数据是地震道且常规统计方法无法检测地层时, 这种方法的效果更加明显。
符号注释:
A(q, θ )— — 自回归部分; B(q, θ )— — 外生变量; CDP— — 共深度点; e(k)— — 一种不稳定的白噪声; F(l, v)— — 趋势剖面的方差; Fq(l)— — 局部波动; h(q)— — 广义Hurst指数; hshuffle(q)— — 混合序列的广义Hurst指数; H— — Hurst指数; i— — 时间序列编号; j— — 包含部分截面的总和; k— — 假定变量和相关系数指数; l— — 时间序列长度; nb— — 多项式的最后指数; N— — 总时间步长数; Nl— — 段数; P(i)— — 截面; Pv(i)— — 拟合多项式; q— — 局部波动次序; RXX(k)— — X时间序列自相关函数; S(ω )— — 功率谱; t— — 时间; T— — 转置; u(k), y(k)— — 信号; X(t)— — 地震总旅行时; Xi— — 时间序列; ŷ (k, θ )— — 线性回归函数; ξ i— — 步长随机变量; τ — — 时间步长变量; ξ N— — 时间步长长度; ω — — 频率; θ — — 系数向量; φ (k)— — 部分信号; υ — — 段。
(编辑 黄昌武)
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|
| [39] |
|
| [40] |
|
| [41] |
|
| [42] |
|
| [43] |
|
| [44] |
|
| [45] |
|
| [46] |
|
| [47] |
|
| [48] |
|
| [49] |
|
| [50] |
|
| [51] |
|
| [52] |
|
| [53] |
|
| [54] |
|
| [55] |
|
| [56] |
|
| [57] |
|
| [58] |
|
| [59] |
|
| [60] |
|
| [61] |
|
| [62] |
|
| [63] |
|
| [64] |
|
| [65] |
|
| [66] |
|
| [67] |
|
| [68] |
|
| [69] |
|
| [70] |
|
| [71] |
|
| [72] |
|
| [73] |
|