引用本文
洪迪峰, 唐雪平, 高文凯, 毛为民, 王鹏, 刘珂. 基于邻井相对位置的井眼分离系数计算方法[J]. 石油勘探与开发, 2020,47(1): 186-192.
HONG Difeng, TANG Xueping, GAO Wenkai, MAO Weimin, WANG Peng, LIU Ke. A new calculation approach of wellbore separation factor based on the relative position of adjacent wells[J]. Petroleum Exploration & Development, 2020,47(1): 186-192.  
Doi: 10.11698/PED.2020.01.18
Permissions
Copyright©2020, 石油勘探与开发》编辑部
石油勘探与开发》编辑部 所有
基于邻井相对位置的井眼分离系数计算方法
洪迪峰, 唐雪平, 高文凯, 毛为民, 王鹏, 刘珂
中国石油集团工程技术研究院有限公司,北京 102206

第一作者简介：洪迪峰（1983-）,男,浙江绍兴人,博士,中国石油集团工程技术研究院有限公司高级工程师,主要从事力学和井下控制工程方面的研究。地址：北京市昌平区黄河街5号院1号楼,邮政编码：102200。E-mail：hdfdr@cnpc.com.cn

收稿日期: 2019-06-21
基金项目: 中国科学院战略性先导科技专项（XDA14020500）; 中国石油天然气集团有限公司科技重大专项（2019A-3912,2018E-2107）
摘要

针对现有井眼分离系数计算方法存在的不足,提出了基于邻井相对位置的井眼分离系数计算方法（简称相对位置法）,并进行了算例分析。在轨迹误差椭球模型的基础上,考虑邻井轨迹误差的相关性,推导了邻井相对误差椭球的计算公式,提出了基于邻井相对位置的分离系数计算公式,并利用共轭梯度法进行求解。算例分析表明,与椭球缩放法和椭球间距法相比,相对位置法计算结果更加精确,适用性更强,能更合理地评价井眼交碰状态。采用提出的方法进行大批量计算,并结合相应的防碰技术规范要求,可以快速简便地寻找关键设计参数的许用范围,在丛式井和定向井设计中具有较好的应用价值。图6表3参24

关键词: 井眼分离系数; 井眼防碰; 邻井轨迹误差; 共轭梯度法; 丛式井
中图分类号:TE21 文献标志码:A 文章编号:1000-0747(2020)01-0186-07
A new calculation approach of wellbore separation factor based on the relative position of adjacent wells
HONG Difeng, TANG Xueping, GAO Wenkai, MAO Weimin, WANG Peng, LIU Ke
CNPC Engineering Technology R&D Company Limited, Beijing 102206, China
Abstract

As the current calculation methods for wellbore separation factor have some deficiencies, a new calculation approach for wellbore separation factor based on the relative position of adjacent wellbores, named as relative position method for short, was proposed and analyzed. Based on the trajectory error ellipsoid model of single wellbore, the error ellipsoids model of adjacent wellbore was derived considering the correlation of trajectory errors between adjacent wells. Furthermore, the calculation formula of the separation factor based on relative position of adjacent wellbore was derived and solved with the conjugate gradient algorithm. Case study shows that the new approach is more precise and higher in applicability than the ellipsoid scalar method and the minimum distance method, it can evaluate the state of well collision more reasonably. By doing batch calculation with the new method and following the criterion of well collision avoidance, the permissible ranges of key parameters in the well design can be worked out quickly. This method has good application in the design of cluster wells and directional wells.

Keyword: wellhole separation factor; wellhole collision avoidance; relative wellbores error; conjugate gradient algorithm; cluster wells
0 引言

丛式井可节约油气资源开发投入, 减少土地资源占用和环境污染, 在海洋和陆地钻井中均有广泛的应用。随着油田的开发, 丛式井和加密井数量不断增加, 井眼空间距离越来越小, 对井眼防碰技术提出了更高的要求。中国制定了行业标准[1], 国外井眼测量精度工业导向委员会（ISCWSA）也长期致力于井眼防碰工作[2]。井眼防碰技术主要应用于丛式井、加密井和定向井等的钻前设计和实钻监测, 可用于评价轨道设计的合理性, 也可用于实时监测钻头与邻井的交碰情况, 进行风险预警。

井眼防碰评价方法以井距扫描计算和轨迹测量误差分析为基础, 评价指标包括邻井最近距离[3, 4]、井眼分离系数[3, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]和井眼交碰概率[3, 17, 18, 19]等。其中, 井眼分离系数综合考虑了邻井距离和井眼轨迹误差的影响, 评价结果比邻井最近距离可靠, 计算过程比井眼交碰概率简单, 是目前国内外普遍采用的评价指标。

现有的井眼分离系数计算方法主要有传统分离系数法、中心向量法[3, 13]、垂足线法[3, 13]、定向分离系数法[6, 7, 8, 9, 10, 12, 14, 16]、椭球缩放法[13, 20]和椭球间距法[21]等。

研究表明, 传统分离系数法和垂足线法的评价结果过于保守[3, 13], 中心向量法和定向分离系数法的评价结果又过于乐观[3, 13, 20], 椭球缩放法和椭球间距法能够获得比较客观的评价结果[13, 20, 21], 但是理论完备性和计算精度方面仍然存在不足。在理论完备性方面, 现有计算方法独立计算轨迹坐标和误差椭球, 再研究邻井误差椭球的相对位置与几何关系, 没有考虑邻井轨迹误差的相关性。在计算精度方面, 采用邻井距离扫描方法（法面距离扫描、最近距离扫描和水平距离扫描）建立邻井轨迹深度对应关系, 计算各深度的分离系数后再寻找最小值, 但这种方法得到的最小值不一定是全局最小值。为了完善理论模型、提高计算精度, 提出了基于邻井相对位置的分离系数理论公式和计算方法（简称相对位置法）, 考虑邻井轨迹误差的相关性, 并采用共轭梯度法求解全局最小值, 以期更客观地评价邻井轨迹之间的空间分离程度, 更好地满足密集丛式井设计和钻井防碰分析的应用需要。

1 计算方法

计算井眼分离系数主要包括3个步骤：①分别计算比较井和参考井的井眼轨迹和轨迹不确定性; ②计算比较井相对参考井的相对位置和相对位置不确定性; ③计算比较井和参考井之间的井眼分离系数。

1.1 单井的井眼轨迹和轨迹不确定性

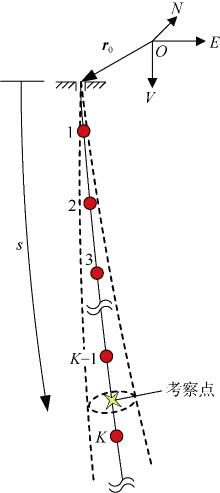
以北东地为全局坐标系, 依据国内外行业标准[22, 23], 采用最小曲率法计算井眼轨迹坐标。如图1所示, 考察点落在井眼轨迹的第K-1个与第$K$个测点间, 坐标矢量为：

$\mathbf{r}={{\mathbf{r}}_{K-1}}+\left( U{{\mathbf{\tau }}_{K-1}}+V{{\mathbf{\tau }}_{K}} \right)\Delta {{L}_{K}}$ （1）

图1 单井的井眼轨迹和轨迹不确定性

其中 ${{\mathbf{\tau }}_{k}}={{\left[ \begin{matrix} \sin {{I}_{k}}\cos {{A}_{k}} & \sin {{I}_{k}}\sin {{A}_{k}} & \cos {{I}_{k}} \\ \end{matrix} \right]}^{\text{T}}}$

（k=1, 2, …, K）

$\Delta {{L}_{k}}={{L}_{k}}-{{L}_{k-1}}$

${{\mathbf{r}}_{k}}={{\mathbf{r}}_{0}}+\sum\limits_{j=1}^{k}{\Delta {{L}_{j}}\left( {{\mathbf{\tau }}_{j-1}}+{{\mathbf{\tau }}_{j}} \right){\tan \left( {{\theta }_{j}}/2 \right)}/{{{\theta }_{j}}}\; }$

${{\theta }_{k}}=\arccos \left( \mathbf{\tau }_{k-1}^{\text{T}}{{\mathbf{\tau }}_{k}} \right)$

$U={\left[ \cos \left( {{\theta }_{K}}-\xi {{\theta }_{K}} \right)-\cos {{\theta }_{K}} \right]}/{\left( {{\theta }_{K}}\sin {{\theta }_{K}} \right)}\; $

$V={\left[ 1-\cos \left( \xi {{\theta }_{K}} \right) \right]}/{\left( {{\theta }_{K}}\sin {{\theta }_{K}} \right)}\; $

$\xi ={\left( s-{{L}_{K-1}} \right)}/{\Delta {{L}_{K}}}\; $

为计算简便, 采用平衡正切法计算轨迹不确定性。研究表明, 基于平衡正切法计算轨迹不确定性能够保证计算精度[11]。轨迹上任意点的坐标是井口坐标、测点数据和考察点局部坐标的函数。忽略井口坐标和考察点局部坐标的误差, 测点数据误差采用ISCWSA误差模型[2], 轨迹误差表示为：

$\text{ }\!\!\delta\!\!\text{ }\mathbf{r}=\sum\limits_{k=1}^{K}{\frac{\partial \mathbf{r}}{\partial {{\mathbf{p}}_{k}}}\text{ }\!\!\delta\!\!\text{ }{{\mathbf{p}}_{k}}}=\sum\limits_{i}{\sum\limits_{k=1}^{K}{{{\mathbf{e}}_{i, k}}{{u}_{i, k}}}}$ （2）

其中 ${{\mathbf{e}}_{i, k}}=\frac{\partial \mathbf{r}}{\partial {{\mathbf{p}}_{k}}}\frac{\partial {{\mathbf{p}}_{k}}}{\partial {{\varepsilon }_{i}}}{{\sigma }_{i, k}}$ $\frac{\partial \mathbf{r}}{\partial {{\mathbf{p}}_{k}}}=\left[ \begin{matrix} \frac{\partial \mathbf{r}}{\partial {{L}_{k}}} & \frac{\partial \mathbf{r}}{\partial {{I}_{k}}} & \frac{\partial \mathbf{r}}{\partial {{A}_{k}}} \\ \end{matrix} \right]$

$\frac{\partial \mathbf{r}}{\partial {{L}_{k}}}=\frac{1}{2}\left\{ \begin{align} & \left( {{\mathbf{\tau }}_{k-1}}-{{\mathbf{\tau }}_{k+1}} \right)\quad k< K-1 \\ & \left[ {{\mathbf{\tau }}_{K-2}}-\xi {{\mathbf{\tau }}_{K-1}}+\left( 1-\xi \right){{\mathbf{\tau }}_{K}} \right]\ k=K-1 \\ & \xi \left( {{\mathbf{\tau }}_{K-1}}+{{\mathbf{\tau }}_{K}} \right)\quad k=K \\ \end{align} \right.$

$\frac{\partial \mathbf{r}}{\partial {{I}_{k}}}=\frac{\partial {{\mathbf{\tau }}_{k}}}{\partial {{I}_{k}}}\left\{ \begin{align} & \left( {{L}_{k+1}}-{{L}_{k-1}} \right)k< K-1 \\ & \left( s-{{L}_{k-1}} \right)k=K-1, K \\ \end{align} \right.$

$\frac{\partial \mathbf{r}}{\partial {{A}_{k}}}=\frac{\partial {{\mathbf{\tau }}_{k}}}{\partial {{A}_{k}}}\left\{ \begin{align} & \left( {{L}_{k+1}}-{{L}_{k-1}} \right)k< K-1 \\ & \left( s-{{L}_{k-1}} \right)k=K-1, K \\ \end{align} \right.$

$\frac{\partial {{\mathbf{\tau }}_{k}}}{\partial {{I}_{k}}}={{\left[ \begin{matrix} \cos {{I}_{k}}\cos {{A}_{k}} & \cos {{I}_{k}}\sin {{A}_{k}} & -\sin {{I}_{k}} \\ \end{matrix} \right]}^{\text{T}}}$

$\frac{\partial {{\mathbf{\tau }}_{k}}}{\partial {{A}_{k}}}={{\left[ \begin{matrix} -\sin {{I}_{k}}\sin {{A}_{k}} & \sin {{I}_{k}}\cos {{A}_{k}} & 0 \\ \end{matrix} \right]}^{\text{T}}}$

测量误差项共有5种类型, 分别为随机误差、系统误差、井间误差、全局误差和偏移误差[11]。区分误差类型是为了计算随机变量的相关性。这5类误差项的相关系数如表1所示。

表1 5类误差项对应随机变量的相关系数

由随机数学相关定理可知, δ r为三维随机向量, 满足三维高斯分布规律, 其概率分布等值面为椭球面, 椭球特征矩阵即为δ r的协方差矩阵[11], 表达式为：

$\mathbf{C}\left( s \right)=\mathbf{C}_{\text{rand}}^{{}}+\mathbf{C}_{\text{syst}}^{{}}+\mathbf{C}_{\text{well}}^{{}}+\mathbf{C}_{\text{glob}}^{{}}+\mathbf{C}_{\text{bias}}^{{}}$ （3）

其中$\mathbf{C}_{\text{rand}}^{{}}=\sum\limits_{i\in R}{\sum\limits_{k}{{{\mathbf{e}}_{i, k}}\mathbf{e}_{i, k}^{\text{T}}}}$

$\mathbf{C}_{\text{syst}}^{{}}=\sum\limits_{i\in S}{\sum\limits_{S}{\left[ \left( \sum\limits_{\forall S}{{{\mathbf{e}}_{i, k}}} \right){{\left( \sum\limits_{\forall S}{{{\mathbf{e}}_{i, k}}} \right)}^{\text{T}}} \right]}}$

$\mathbf{C}_{\text{well}}^{{}}=\sum\limits_{i\in W}{\left[ \left( \sum\limits_{k}{{{\mathbf{e}}_{i, k}}} \right){{\left( \sum\limits_{k}{{{\mathbf{e}}_{i, k}}} \right)}^{\text{T}}} \right]}$

$\mathbf{C}_{\text{glob}}^{{}}=\sum\limits_{i\in G}{\left[ \left( \sum\limits_{k}{{{\mathbf{e}}_{i, k}}} \right){{\left( \sum\limits_{k}{{{\mathbf{e}}_{i, k}}} \right)}^{\text{T}}} \right]}$

$\mathbf{C}_{\text{bias}}^{{}}=\left( \sum\limits_{i\in B}{\sum\limits_{k}{{{\mathbf{e}}_{i, k}}}} \right){{\left( \sum\limits_{i\in B}{\sum\limits_{k}{{{\mathbf{e}}_{i, k}}}} \right)}^{\text{T}}}$

（3）式中, 系统误差的协方差矩阵计算比较特殊, 需要按照测量工具进行累加。首先累加特定误差项在同一套测量工具内的所有误差向量, 然后计算该测量工具所有测点的协方差矩阵, 最后累加全部测量工具的协方差矩阵。

对应的井眼轨迹误差椭球方程为：

${{\mathbf{r}}^{\text{T}}}{{\mathbf{C}}^{-1}}\mathbf{r}={{\lambda }^{2}}$ （4）

椭球放大因子λ 与置信概率Pb相关[17]：

${{P}_{\text{b}}}=\sqrt{{2}/{\text{ }\!\!\pi\!\!\text{ }}\; }\int_{0}^{\lambda }{{{r}^{2}}\exp \left( -{{{r}^{2}}}/{2}\; \right)\text{d}r}$ （5）

（5）式可采用数值积分计算。椭球放大因子1.0, 1.5, 2.0, 2.5, 3.0和4.0对应的置信概率分别为19.9%, 47.8%, 73.9%, 90.0%, 97.1%和99.9%。在井眼轨迹的误差分析中, 通常取椭球放大因子为2.0~3.0。本文中取椭球放大因子为2.5, 此时井眼位置落入误差椭球内的概率约为90%。

1.2 邻井的相对位置和相对位置不确定性

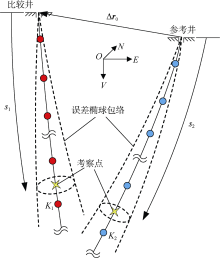
按照（1）式计算比较井和参考井上考察点（见图2）的坐标r1和r2, 则比较井相对参考井的相对位置为：

$\mathbf{d}\left( {{s}_{1}}, {{s}_{2}} \right)={{\mathbf{r}}_{1}}\left( {{s}_{1}} \right)-{{\mathbf{r}}_{2}}\left( {{s}_{2}} \right)$ （6）

图2 邻井的相对位置和相对位置不确定性

根据ISCWSA误差模型, 井眼轨迹相对位置的误差也满足三维高斯分布规律, 其概率分布等值面为椭球面, 其协方差矩阵[11]为：

$\mathbf{C}\left( {{s}_{1}}, {{s}_{2}} \right)={{\mathbf{C}}_{1}}\left( {{s}_{1}} \right)+{{\mathbf{C}}_{2}}\left( {{s}_{2}} \right)-\mathbf{D}_{\text{glob}}^{{}}-\mathbf{D}_{\text{bias}}^{{}}$ （7）

（7）式中, C1(s1)和C2(s2)按照（3）式进行计算, Dglob和Dbias按照以下公式计算：

$\mathbf{D}_{\text{glob}}^{{}}=\sum\limits_{i\in G}{\left( \sum\limits_{k}{\mathbf{e}_{i, k, 2}^{{}}}\sum\limits_{k}{\mathbf{e}{{_{i, k, 1}^{{}}}^{\text{T}}}}+\sum\limits_{k}{\mathbf{e}_{i, k, 1}^{{}}}\sum\limits_{k}{\mathbf{e}{{_{i, k, 2}^{{}}}^{\text{T}}}} \right)}$ （8）

$\mathbf{D}_{\text{bias}}^{{}}=\sum\limits_{i\in B}{\sum\limits_{k}{\mathbf{e}_{i, k, 2}^{{}}}}\sum\limits_{i\in B}{\sum\limits_{k}{\mathbf{e}{{_{i, k, 1}^{{}}}^{\text{T}}}}}+\sum\limits_{i\in B}{\sum\limits_{k}{\mathbf{e}_{i, k, 1}^{{}}}}\sum\limits_{i\in B}{\sum\limits_{k}{\mathbf{e}{{_{i, k, 2}^{{}}}^{\text{T}}}}}$ （9）

考虑井径和防碰安全余量[2, 8], 比较井和参考井上两个考察点之间的分离系数为：

$f\left( {{s}_{1}}, {{s}_{2}} \right)=\frac{1}{\lambda }\left( 1-\frac{{{d}_{\text{s}}}}{\left\| \mathbf{d} \right\|} \right)\sqrt{{{\mathbf{d}}^{\text{T}}}{{\mathbf{C}}^{-1}}\mathbf{d}}$ （10）

其中 ${{d}_{\text{s}}}={\left( {{D}_{1}}+{{D}_{2}} \right)}/{2}\; +{{d}_{0}}$

比较井和参考井之间的分离系数即为（10）式的全局最小值：

${{F}_{\text{s}}}=\underset{{{s}_{1}}, {{s}_{2}}}{\mathop{\min }}\, \frac{1}{\lambda }\left( 1-\frac{{{d}_{\text{s}}}}{\left\| \mathbf{d} \right\|} \right)\sqrt{{{\mathbf{d}}^{\text{T}}}{{\mathbf{C}}^{-1}}\mathbf{d}}$ （11）

1.3 相对位置法井眼分离系数计算方法

（11）式给出了相对位置法井眼分离系数的计算公式, 这是一个二维非线性最小值问题, 采用共轭梯度法进行求解。目标函数为：

$\min f\left( {{s}_{1}}, {{s}_{2}} \right)=\frac{1}{\lambda }\left( 1-\frac{{{d}_{\text{s}}}}{\left\| \mathbf{d} \right\|} \right)\sqrt{{{\mathbf{d}}^{\text{T}}}{{\mathbf{C}}^{-1}}\mathbf{d}}$ （12）

根据Richard外推法计算目标函数的梯度：

$\mathbf{g}\left( {{s}_{1}}, {{s}_{2}} \right)={{\left[ \begin{matrix} {\partial f}/{\partial {{s}_{1}}}\; & {\partial f}/{\partial {{s}_{2}}}\; \\ \end{matrix} \right]}^{\text{T}}}$ （13）

其中

$\frac{\partial f}{\partial {{s}_{1}}}\approx \frac{1}{6h}\left[ 8f\left( {{s}_{1}}+h, {{s}_{2}} \right)-f\left( {{s}_{1}}+2h, {{s}_{2}} \right)-7f\left( {{s}_{1}}, {{s}_{2}} \right) \right]$

$\frac{\partial f}{\partial {{s}_{2}}}\approx \frac{1}{6h}\left[ 8f\left( {{s}_{1}}, {{s}_{2}}+h \right)-f\left( {{s}_{1}}, {{s}_{2}}+2h \right)-7f\left( {{s}_{1}}, {{s}_{2}} \right) \right]$

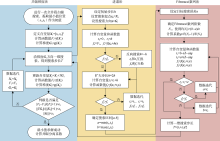
相对位置法井眼分离系数的计算流程如图3所示。为初步定位全局最小值位置, 先进行一次全井段的扫描搜索, 由扫描结果中的最小值位置作为共轭梯度法的初值。一般取扫描间隔30 m, 如果一些特殊井段变化过于剧烈, 则需要适当减小扫描间隔。该计算流程中, 共轭梯度法是主流程, 进退法和Fibonacci数列法组成了一维搜索算法。采用进退法可以快速确定最小值区间, 而采用Fibonacci数列法可以快速精确定位最小值, 这两者配合组成的一维搜索算法具有稳定性强、搜索速度快和计算精度高等优点。

图3 相对位置法井眼分离系数的计算流程

1.4 最小分离系数扫描法

在全井段扫描搜索中, 本文推荐采用最小分离系数扫描法, 以便更快初步定位全局最小值。该扫描法的数学问题表述为：选定比较井上考察点, 寻找参考井上的对应点, 使两点之间分离系数最小, 即：

$\min f\left( {{s}_{2}} \right)=\frac{1}{\lambda }\left( 1-\frac{{{d}_{\text{s}}}}{\left\| \mathbf{d} \right\|} \right)\sqrt{{{\mathbf{d}}^{\text{T}}}{{\mathbf{C}}^{-1}}\mathbf{d}}$ （14）

该问题直接采用图3所示的一维搜索算法计算。

2 算例分析
2.1 算例1

某油田采用三维丛式水平井开发[21], 其中比较井与参考井的井口坐标偏差：Δ N0为4.10 m, Δ E0为9.10 m, Δ V0为0.09 m。参考井只有1套方案, 比较井有2套方案, 它们的轨道设计数据如表2所示。设计采用MWD（随钻测量）进行轨迹监测, 计算模型包括25项误差源[24], 取椭球放大因子为2.5, 忽略井径和防碰安全余量。

表2 井眼轨道设计数据和误差椭球

在表2中轨道设计关键点的基础上, 以30 m为测段长度, 分别计算各测点的轨迹坐标和轨迹不确定性。限于篇幅, 本文只列举了轨道设计关键点的坐标、误差椭球半轴长度和姿态欧拉角, 如表2所示。计算井间分离系数时, 以30 m为步长进行一次全井段扫描, 提取分离系数最小值位置作为共轭梯度法初值, 根据图3所示流程进行计算。

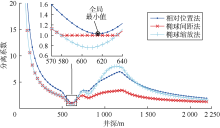
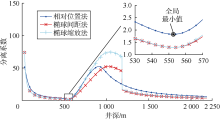
文献[20]比较研究了等效误差椭球法、中心向量法、椭球缩放法和传统分离系数法的分析结果, 认为传统分离系数法过于保守, 等效误差椭球法和中心向量法过于乐观, 椭球缩放法结果居中。文献[21]比较研究了定向分离系数法、中心向量法、椭球间距法、垂足线法和传统分离系数法的分析结果, 认为中心向量法和定向分离系数法计算结果偏乐观, 传统分离系数法和垂足线法结果偏保守, 椭球间距法在5种方法中居中。基于以上文献调研结果, 认为椭球缩放法和椭球间距法能够获得比较客观的评价结果, 因此本文进一步比较相对位置法、椭球缩放法和椭球间距法。分别采用相对位置法、椭球缩放法和椭球间距法计算井眼分离系数, 结果如表3、图4和图5所示。可以看出：①相对位置法、椭球缩放法和椭球间距法的计算结果总体接近, 但椭球缩放法和椭球间距法结果仍旧偏保守。②当误差椭球不相交时, 椭球缩放法和椭球间距法的结果一致; 当误差椭球相交时, 椭球间距法失效, 分离系数为1, 椭球缩放法仍有效。③椭球缩放法和椭球间距法采用最近距离扫描法, 分离系数随井深可能出现跳变, 如图5中井深1 183 m处; 相对位置法采用最小分离系数扫描法, 分离系数随井深连续变化。综合以上比对分析, 认为与椭球缩放法和椭球间距法相比, 相对位置法计算结果更加精确, 适用性更强, 能够更合理地评价井眼交碰状态。

表3 椭球缩放法、椭球间距法和相对位置法的计算结果对比

图4 比较井A与参考井的井眼分离系数

图5 比较井B与参考井的井眼分离系数

2.2 算例2

研究算例1中比较井B的布井位置对分离系数的影响。比较井B相对参考井的井口坐标：Δ N0为-15~15 m, Δ E0为-20~20 m, Δ V0为0.09 m。同样设计采用MWD进行轨迹监测, 计算模型包括25项误差源[24], 取椭球放大因子为2.5。

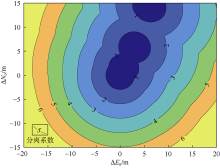
以0.25 m为步长, 南北方向插值121个点, 东西方向插值161个点, 共计算121× 161=19 481组布井位置时的井眼分离系数。采用C++编写计算程序, 在普通个人计算机上进行计算, 采用CPU型号为Intel Core i7-8700, 主频3.0 GHz, 总共计算用时约10 min, 平均每组计算耗时约30 ms, 计算速度较快。分离系数图版如图6所示。

图6 比较井B井口位置对应的分离系数

国外依据井眼分离系数划分了井眼交碰风险等级, 制定了相应的防碰技术规范[6, 9]。通常情况下, Fs> 5.0时可以安全钻进, 1.5< Fs≤ 5.0时需要警戒和实时监测, 1.0< Fs≤ 1.5时建议关闭邻井, Fs≤ 1.0时要求停钻, 直至危险消除。按照这一要求, 布井位置应该选择分离系数大于5.0的区域, 这在图6中可以快速查找。

采用本文的方法进行大批量计算, 再结合防碰技术规范, 可以快速简便地寻找关键设计参数的许用范围, 并不局限于井口位置, 也可用于井段设计和靶点设计等, 对丛式井的井眼防碰设计具有重要的应用价值。

3 结语

本文提出的相对位置法采用邻井相对位置的误差椭球计算分离系数, 考虑了邻井轨迹误差的相关性, 完善了井眼分离系数的理论模型。

传统井眼分离系数评价方法采用邻井距离扫描方法寻找到的最小分离系数不一定是全局最小值, 而相对位置法采用共轭梯度法求解全局最小值, 是一种更加实用、快速、精确的求解方法。

符号注释：

a, b— — 搜索区间下限和上限, m; Ak— — 第k个测点的方位角, rad; B, G, R, S, W— — 偏移误差、全局误差、随机误差、系统误差、井间误差项序号集合; C(s)— — 指定深度点的轨迹误差协方差矩阵; C(s1, s2)— — 相对轨迹误差协方差矩阵; C1(s1)— — 比较井在井深s1处的轨迹误差协方差矩阵; C2(s2)— — 参考井在井深s2处的轨迹误差协方差矩阵; Cbias, Cglob, Crand, Csyst, Cwell— — 指定深度点的偏移误差、全局误差、随机误差、系统误差、井间误差协方差矩阵; d(s1, s2)— — 比较井相对参考井的轨迹坐标矢量; d0— — 比较井和参考井之间的防碰安全余量, m; D1, D2— — 比较井和参考井的井径, m; Dbias— — 比较井和参考井的偏移误差互相关矩阵; Dglob— — 比较井和参考井的全局误差互相关矩阵; e— — 目标搜索误差, m; e1, e2, e3— — 迭代精度; ei, k— — 第k个测点第i个误差项的误差向量; ei, k, 1, ei, k, 2— — 比较井和参考井上第k个测点第i个误差项的误差向量; f(s1, s2)— — 比较井和参考井上两个考察点之间的分离系数; Fs— — 比较井和参考井之间的分离系数; g(s1, s2)— — 分离系数随深度变化的梯度向量; h— — Richard外推法所用的微分步长, 一般取1× 10-6~1× 10-3 m; i— — 误差项序号; Ik— — 第k个测点的井斜角, rad; j— — 次级测点序号; k— — 测点序号; K— — 轨迹考察点所在测段末端的测点序号; K1, K2— — 比较井和参考井上轨迹考察点所在测段末端的测点序号; Lk— — 第k个测点的井深, m; Δ Lk— — 第k-1个与第k个测点间测段的长度, m; N, E, V— — 北、东、地坐标, m; Nf— — Fibonacci数列阶数; N0, E0, V0— — 井口北、东、地坐标, m; Δ N0, Δ E0, Δ V0— — 比较井相对参考井的井口北、东、地坐标, m; pk— — 第k个测点的测量数据向量, pk=[Lk Ik Ak]T; δ pk— — 第k个测点的测量误差向量; ${\partial {{\mathbf{p}}_{k}}}/{\partial {{\varepsilon }_{i}}}\; $— — 第k个测点对第i个误差项的权函数, 由ISCWSA误差模型给定; Pb— — 置信概率, 即井眼位置落入误差椭球内的概率; q— — 系数; r— — 井眼半径, m; r— — 轨迹考察点的坐标矢量; δ r— — 指定深度点的轨迹误差向量; r0— — 井口坐标矢量, r0=[N0E0V0]T; Δ r0— — 比较井相对参考井的井口坐标矢量, Δ r0=[Δ N0 Δ E0 Δ V0]T; r1, r2— — 比较井和参考井上轨迹考察点的坐标矢量; rk— — 第k个测点的坐标矢量; s— — 轨迹考察点的井深, m; s— — 搜索方向矢量; s1, s2— — 比较井和参考井上轨迹考察点的井深, m; T— — 搜索步长, m; ui, k— — 第k个测点第i个误差项对应的随机变量, 该随机变量满足高斯分布, 数学期望为0, 方差为1; θ k— — 第k-1个与第k个测点间测段的圆弧角度, rad; λ — — 椭球放大因子; ξ — — 轨迹考察点在测段内的相对深度; ξ 1, ξ 2— — 比较井和参考井上轨迹考察点在测段内的相对深度; σ i, k— — 第k个测点第i个误差项的幅值, 由ISCWSA误差模型给定; τ k— — 第k个测点的井眼轴线矢量。

（编辑 胡苇玮）

参考文献
[1] 国家能源局. 丛式井平台布置及井眼防碰技术要求: SY/T 6396—2014[S]. 北京: 石油工业出版社, 2015.
National Energy Administration. Slot layout and anti-collision technical requirements of platform cluster well drilling: SY/T 6396—2014[S]. Beijing: Petroleum Industry Press, 2015. [本文引用:1]
[2] Industry Steering Committee on Wellbore Survey Accuracy. Collision avoidance calculations: Current common practice[EB/OL]. (2013-10-02)[2019-05-20]. https://www.iscwsa.net/articles/collision-avoidance-calculations-current-common-practice/. [本文引用:3]
[3] JAMIESON A. Introduction to wellbore positioning: An ISCWSA initiative[EB/OL]. (2017-09-10)[2019-06-10]. https://www.uhi.ac.uk/en/t4-media/one-web/university/research/eBook_V9_10_2017-redux.pdf. [本文引用:7]
[4] 中国石油天然气集团公司. 密集丛式井上部井段防碰设计与施工技术规范: Q/SY 1296—2010[S]. 北京: 石油工业出版社, 2010.
China National Petroleum Corporation. Specifications of anti-collision design and construction for upper section of dense cluster well: Q/SY 1296—2010[S]. Beijing: Petroleum Industry Press, 2010. [本文引用:1]
[5] DE WARDT J P, MULLIN S, THOROGOOD J, et al. Well bore collision avoidance and interceptions: State of the art[R]. SPE 0313-0042-JPT, 2013. [本文引用:1]
[6] POEDJONO B, PHILLIPS W J, LOMBARDO G J. Anti-collision risk management stand ard for well placement[R]. SPE 121040-MS, 2009. [本文引用:3]
[7] POEDJONO B, CONRAN G, AKINNIRANYE G, et al. Minimizing the risk of well collisions in land and offshore drilling[R]. SPE 108279-MS, 2007. [本文引用:2]
[8] POEDJONO B, AVILA C M, VAN CHINH P, et al. Case studies in the application of an effective anticollision risk management stand ard[R]. SPE 126722-MS, 2010. [本文引用:3]
[9] POEDJONO B, AKINNIRANYE G, CONRAN G, et al. Well-collision risk in congested environments[R]. SPE 101719-MS, 2006. [本文引用:3]
[10] POEDJONO B, AKINNIRANYE G, CONRAN G, et al. A comprehensive approach to well-collision avoidance[R]. Houston, Texas: 2007 AADE National Technical Conference, 2007. [本文引用:2]
[11] WILLIAMSON H S. Accuracy prediction for directional measurement while drilling[J]. SPE Drilling & Completion, 2013, 15(4): 221-233. [本文引用:5]
[12] WILLIAMSON H S. Towards risk-based well separation rules[J]. SPE Drilling & Completion, 1998, 13(1): 47-51. [本文引用:2]
[13] SAWARYN S J, JAMIESON A, MCGREGOR A E. Explicit calculation of expansion factors for collision avoidance between two co-planar survey error ellipses[J]. SPE Drilling & Completion, 2012, 28(1): 75-85. [本文引用:7]
[14] MCNAIR G A, LANCE S J, CODLING J, et al. Implementation of a new risk based well collision avoidance method[R]. SPE 92554-MS, 2005. [本文引用:2]
[15] CHENG K, CHENG Z, WEI Y, et al. China offshore anti-collision risk management stand ard and remedial measures[R]. SPE 141089-MS, 2011. [本文引用:1]
[16] 刁斌斌, 高德利. 邻井定向分离系数计算方法[J]. 石油钻探技术, 2012, 40(1): 22-27.
DIAO Binbin, GAO Deli. Calculation method of adjacent well oriented separation factor[J]. Petroleum Drilling Techniques, 2012, 40(1): 22-27. [本文引用:2]
[17] 柳贡慧, 董本京, 高德利. 误差椭球(圆)及井眼交碰概率分析[J]. 钻采工艺, 2000, 23(3): 7-14.
LIU Gonghui, DONG Benjing, GAO Deli. Probability analysis of error ellipsoid (ellipse) and hole intersection[J]. Drilling & Production Technology, 2000, 23(3): 7-14. [本文引用:2]
[18] BROOKS A G, WILSON H. An improved method for computing wellbore position uncertainty and its application to collision and target intersection probability analysis[R]. SPE 36863-MS, 1996. [本文引用:1]
[19] BROOKS A G. A new look at wellbore collision probability[R]. SPE 116155-MS, 2008. [本文引用:1]
[20] 史玉才, 张晨, 薛磊, 等. 井眼分离系数计算新方法[J]. 石油学报, 2015, 36(12): 1580-1585.
SHI Yucai, ZHANG Chen, XUE Lei, et al. A new calculation method of wellbore separation factor[J]. Acta Petrolei Sinica, 2015, 36(12): 1580-1585. [本文引用:4]
[21] 唐宁, 王少萍, 洪迪峰. 井眼测量误差椭球最小间距计算方法[J]. 石油学报, 2017, 38(11): 1320-1325.
TANG Ning, WANG Shaoping, HONG Difeng. A calculation method of minimum distance between wellbore survey error ellipsoids[J]. Acta Petrolei Sinica, 2017, 38(11): 1320-1325. [本文引用:4]
[22] 国家能源局. 定向井轨道设计与轨迹计算: SY/T 5435—2012[S]. 北京: 石油工业出版社, 2012.
National Energy Administration. Wellpath planning & trajectory calculation for directional wells: SY/T 5435—2012[S]. Beijing: Petroleum Industry Press, 2012. [本文引用:1]
[23] API. Directional drilling survey calculation methods and terminology: API Bulletin D20[S]. Washington D. C. : API, 1985. [本文引用:1]
[24] ISCWSA Sub-Committees. ISCWSA MWD error model revision 4[EB/OL]. (2015-06-05)[2019-04-16]. https://www.iscwsa.net/articles/iscwsa-mwd-error-model-revision-4/. [本文引用:2]