基于多井模型的压裂参数-开发井距系统优化
[王军磊
, 贾爱林, 位云生, 贾成业, 齐亚东, 袁贺, 金亦秋]
, 贾爱林, 位云生, 贾成业, 齐亚东, 袁贺, 金亦秋]
引用本文
王军磊, 贾爱林, 位云生, 贾成业, 齐亚东, 袁贺, 金亦秋. 基于多井模型的压裂参数-开发井距系统优化[J]. 石油勘探与开发, 2019,46(5): 981-992.
WANG Junlei, JIA Ailin, WEI Yunsheng, JIA Chengye, QI Yadong, YUAN He, JIN Yiqiu. Optimization workflow for stimulation-well spacing design in a multiwell pad[J]. Petroleum Exploration & Development, 2019,46(5): 981-992.
Doi: 10.11698/PED.2019.05.18WANG Junlei, JIA Ailin, WEI Yunsheng, JIA Chengye, QI Yadong, YUAN He, JIN Yiqiu. Optimization workflow for stimulation-well spacing design in a multiwell pad[J]. Petroleum Exploration & Development, 2019,46(5): 981-992.
Permissions
Copyright©2019, 石油勘探与开发》编辑部
基于多井模型的压裂参数-开发井距系统优化
第一作者简介：王军磊（1986-）,男,山东文登人,博士,中国石油勘探开发研究院工程师,主要从事渗流力学理论、非常规天然气生产动态分析及页岩气地质工程一体化研究。地址：北京市海淀区学院路20号,中国石油勘探开发研究院气田开发研究所,邮政编码：100083。E-mail：wangjunlei@petrochina.com.cn
摘要
以变缝宽导流裂缝为基本流动单元,建立考虑井间干扰和缝间干扰的多水平井渗流数学模型,采用半解析方法求解模型,模拟多井开发平台全生命周期生产动态,分析裂缝长度、裂缝导流能力、井距、缝距等因素对生产效果的影响。在此基础上提出了以压裂规模为内部约束条件,以经济效益为外部约束条件的“嵌套式”全局优化方法来优化水平井-裂缝等钻完井参数。研究表明,不考虑约束条件时,增加裂缝与地层接触面积、降低缝/井间干扰强度、平衡裂缝与地层流入流出关系均能有效提高平台开发效果,但不存在最优钻完井参数。仅考虑内部约束条件时,存在最优裂缝导流能力和长度,但不存在最优井距、缝距。同时考虑内外部约束条件时,裂缝导流能力、裂缝长度、井距、缝距等因素间产生关联,出现参数优化空间,在压裂规模较小时宜采用小井距、宽缝距、短裂缝的水平井部署模式;在压裂规模较大时则宜采用大井距、窄缝距、长裂缝的部署模式。
关键词:
水平井; 多段压裂; 裂缝导流能力; 裂缝长度; 井距; 缝距; 参数优化
中图分类号:TE357
文献标志码:A
文章编号:1000-0747(2019)05-0981-12
Optimization workflow for stimulation-well spacing design in a multiwell pad
Abstract
A flow mathematical model with multiple horizontal wells considering interference between wells and fractures was established by taking the variable width conductivity fractures as basic flow units. Then a semi-analytical approach was proposed to model the production performance of whole life cycle in well pad and to investigate the effect of fracture length, flow capacity, well spacing and fracture spacing on ultimate recovery (EUR). Finally, a workflow of nested optimization with economic profit as the outer constraint and fracturing scale as inner constraint was developed to optimize drilling and completion parameters of the horizontal well fracturing. The results show that, when the constraint conditions aren’t considered, increasing contact area between fracture and formation, reducing interference between fractures/wells, balancing inflow and outflow between fracture and formation all can effectively improve the development effect of the well pad, but there are no best drilling and completion parameters. When only the inner constraint condition is considered, there exists the optimal fracture flow capacity and fracture length. The fracture flow capacity and fracture length, well space, fracture space are correlated when considering both inner and outer constraints for parameter optimization. Small well space, wide fracture space and short fracture should be adopted when the fracturing scale is small. When the fracturing scale is large, big well space, small fracture space and long fracture should be used.
Keyword:
horizontal well; multi-staged fracturing; fracture flow capacity; fracture length; well space; fracture space; parameters optimization
0 引言
水平井钻井及分段压裂技术广泛应用于非常规储集层油气开发。研究表明影响井产能的主控因素众多, 主要分为地层参数、流体参数及钻完井参数[1], 其中地层参数和流体参数是不可控因素, 钻完井参数由工程设计确定, 属于人为可控因素。从油藏工程角度看, 水平井多段压裂的目的是在尽可能增加裂缝与地层接触面积的前提下, 提高裂缝内部的有效导流能力, 降低流动过程中的渗流阻力, 改善生产效果。对于包括多口压裂水平井的开发平台而言, 最主要的设计指标包括井距、段距、支撑剂用量、裂缝长度及导流能力等[2, 3, 4]。
开发平台设计指标优化的难点主要体现在模拟要充分体现缝间干扰、井间干扰、裂缝导流影响下的生产动态特征, 以及厘清主控因素与生产动态的对应关系和主控因素间的关联性。在生产动态模拟方面, 王晓冬等[5]在Chen和Raghavan[6]研究基础上采用均匀流量裂缝和裂缝导流因子的方法获得了非稳态渗流解析解, 解决裂缝间干扰问题, 较好地模拟了单口压裂水平井压力动态特征; Chen等[7]建立了考虑有限导流裂缝空间分布复杂性的地层-裂缝耦合流动模型, 并给出了相应的边界元求解方法, 有效解决了复杂形态裂缝的非稳态渗流问题; 方文超等[8]建立了考虑复杂裂缝跨尺度特性的离散裂缝数值模型, 突破了单井尺度的规模限制, 模拟了包含3口长体积压裂水平井的开发平台生产动态; Yu等[9]采用半解析方法描述了不同井间连通条件下的多口压裂水平井井间响应机制, 重点研究了开发井距对邻井压力干扰响应的影响。在主控因素影响分析方面, 目前多数研究采用单因素控制法逐个分析特定影响因素, 该方法忽略了各因素间的关联性, 分析结果局限性大, 对其他因素随之产生的影响考虑不周[10, 11, 12, 13]; 正交试验、灰色关联等分析手段虽然改进了单因素控制分析法的局限性, 但仍属于多方案设计对比分析方法, 难以全部覆盖最优解空间[14, 15, 16]; 以输出结果为导向的遗传算法、神经网络等智能算法计算量大, 尤其是当井数和压裂段数增加时计算量更大, 不便于推广应用[17, 18]。
水平井-压裂设计参数的同步优化是一项复杂的多参数优化技术, 既是非线性规划的数学问题, 又是涉及多学科交叉的油藏工程问题。本文以变缝宽导流裂缝为基本流动单元, 建立多井系统全生命周期生产动态模型, 并获得产量、累计产量的半解析解; 以此为基础, 将经典支撑剂指数法改进应用至多井/缝的非稳态生产阶段, 同时结合压裂设计和经济评价模型, 约束影响参数的优化空间, 最终形成一套具有油藏工程意义的多参数全局优化方法。
1 多井非稳态产能评价模型
1.1 模型介绍
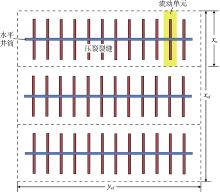
本文以“ 井工厂” 平台的半支为基本研究单元, 为了减小非均质性影响, 平台采用水平井均匀部署、裂缝平行排列的模式, 同时裂缝属性相同（见图1）。水平井以常压生产, 井底压力为pwf。假设储集层为均
质地层, 裂缝高度等于储集层厚度, 裂缝内产出微可压缩流体。气体在致密介质内遵循非线性渗流规律, 根据Ertekin模型, 基质内流动速度可分解为经典达西流和滑脱流[19]：
\[{{v}_{\text{m}}}=\frac{{{K}_{\text{m}}}}{{{\mu }_{\text{g}}}}\left( 1+{{b}_{\text{am}}} \right)\nabla {{p}_{\text{m}}}\ （1）\]
其中 \[{{b}_{\text{am}}}\text{=}\frac{{{D}_{\text{g}}}{{\mu }_{\text{g}}}{{c}_{\text{g}}}{{p}_{\text{m}}}}{{{K}_{\text{m}}}}\frac{1}{{{p}_{\text{m}}}}\]
（1）式中的滑脱速度是由基质内浓度差引起的, 基质与水力裂缝交界面上的浓度差可忽略不计[20], 滑脱效应趋近于零, 即：
.x\[{{b}_{\text{am}}}(x, y)=\left\{ \begin{align} & 0 \ \ 交界面 \ \ \ \ \ \\ & {{b}_{\text{am}}}\ \ 非交界面\ \ \\ \end{align} \right.\ （2）\]
气体流动问题通常引入拟函数变量对非线性流动进行拟线性化处理, 其中裂缝内拟压力、基质内拟压力分别如下式所示：
\[{{m}_{\text{f}}}=\frac{{{\mu }_{\text{gi}}}{{Z}_{\text{gi}}}}{{{p}_{\text{i}}}}\int_{{{p}_{\text{i}}}}^{p}{\frac{\xi }{{{\mu }_{\text{g}}}(\xi ){{Z}_{\text{g}}}(\xi )}\text{d}\xi }\ （3）\]
\[{{m}_{\text{m}}}=\frac{{{\mu }_{\text{gi}}}{{Z}_{\text{gi}}}}{{{p}_{\text{i}}}}\int_{{{p}_{\text{i}}}}^{p}{\frac{{{\gamma }_{\text{m}}}(\xi )\xi }{{{\mu }_{\text{g}}}(\xi ){{Z}_{\text{g}}}(\xi )}\text{d}\xi }\ （4）\]
非线性流动修正因子及与之对应的拟时间分别为：
\[{{\gamma }_{\text{m}}}({{p}_{\text{m}}})=1+{{b}_{\text{am}}}\ （5）\]
\[{{t}_{\text{a}}}=\int_{0}^{t}{\frac{{{\gamma }_{\text{m}}}(\tau ){{\mu }_{\text{gi}}}{{c}_{\text{ti}}}}{{{\mu }_{\text{g}}}(\tau ){{c}_{\text{t}}}(\tau )}\text{d}\tau }=t{{\beta }_{\text{m}}}(t)\ （6）\]
其中 \({{\beta }_{\text{m}}}(t)=\frac{1}{t}\int_{0}^{t}{{{\lambda }_{\text{m}}}(\tau )\text{d}\tau }\) \({{\lambda }_{\text{m}}}(t)=\frac{{{\gamma }_{\text{m}}}(t)}{\frac{{{\mu }_{\text{g}}}(t)}{{{\mu }_{\text{gi}}}}\frac{{{c}_{\text{t}}}(t)}{{{c}_{\text{ti}}}}}\)处理后可以将非线性气体流动在形式上等效转换为线性化液体流动。
 | 图1 平台半分支多口压裂水平井部署示意图 |
由于整个渗流系统处于同一压力系统, 流动过程可分解为连续的裂缝内和地层内流动两部分。对流动全过程进行建模时, 裂缝和地层采用两套独立空间坐标, 通过将两部分流动在裂缝面进行压力和流量耦合, 可得到不同时刻地层任一点的压力和沿裂缝的流量分布。
考虑不同井距条件下水力压裂对裂缝开启的影响, 本文采用变缝宽裂缝模型。当裂缝延展方向平行于最大主应力方向时, 越远离井筒的位置井间应力阴影越显著, 导致裂缝开启所需净压力增加、支撑剂运移受阻, 裂缝宽度自井筒向外呈现递减趋势[21], 如下所示：
\[{{w}_{\text{f}}}({{x}_{\text{hf}}})={{w}_{f, \max }}\left[ -{{({{x}_{\text{hf}}}/{{x}_{\text{f}}})}^{2}}+2({{x}_{\text{hf}}}/{{x}_{\text{f}}}) \right]\ （7）\]
为了便于数学建模, 本文定义无因次压力、无因次产量、无因次累计产量为：
\[{{p}_{\text{mD}}}=\frac{{{m}_{\text{m}}}({{p}_{\text{i}}})-{{m}_{\text{m}}}({{p}_{\text{m}}})}{{{m}_{\text{m}}}({{p}_{\text{i}}})-{{m}_{\text{m}}}({{p}_{\text{wf}}})}\ （8）\]
\[{{p}_{\text{fD}}}=\frac{{{m}_{\text{f}}}({{p}_{\text{i}}})-{{m}_{\text{f}}}({{p}_{\text{f}}})}{{{m}_{\text{m}}}({{p}_{\text{i}}})-{{m}_{\text{m}}}({{p}_{\text{wf}}})}\ （9）\]
\[{{q}_{\text{wD}}}=\frac{\chi {{q}_{\text{w}}}{{\mu }_{\text{gi}}}{{B}_{\text{gi}}}}{{{K}_{\text{m}}}h\left[ {{m}_{\text{m}}}({{p}_{\text{i}}})-{{m}_{\text{m}}}({{p}_{\text{wf}}}) \right]}\ （10）\]
\[{{G}_{\text{pD}}}=\frac{\chi {{B}_{\text{gi}}}{{G}_{\text{p}}}}{h\left[ {{m}_{\text{m}}}({{p}_{\text{i}}})-{{m}_{\text{m}}}({{p}_{\text{wf}}}) \right]{{\phi }_{\text{m}}}{{c}_{\text{ti}}}L_{\text{ref}}^{2}}\ （11）\]
其余无因次时间、无因次长度、无因次导流能力及无因次裂缝流量密度为：
\[{{t}_{\text{D}}}=\psi \frac{{{K}_{\text{m}}}{{t}_{\text{a}}}}{{{\phi }_{\text{m}}}{{\mu }_{\text{gi}}}{{c}_{\text{ti}}}L_{\text{ref}}^{2}}\ （12）\]
\[{{\zeta }_{\text{D}}}=\frac{\zeta }{{{L}_{\text{ref}}}}\ （13）\]
\[{{C}_{\text{fD}}}=\frac{{{K}_{\text{f}}}{{w}_{\text{f}}}}{{{K}_{\text{m}}}{{L}_{\text{ref}}}}\ （14）\]
\[{{q}_{\text{fD}}}=\chi \frac{{{q}_{\text{f}}}{{L}_{\text{ref}}}{{\mu }_{\text{gi}}}{{B}_{\text{gi}}}}{{{K}_{\text{m}}}h\left[ {{m}_{\text{m}}}({{p}_{\text{i}}})-{{m}_{\text{m}}}({{p}_{\text{wf}}}) \right]}\ （15）\]
其中χ , ψ 为单位转换系数。当采用SI单位制时, χ = 0.5/π , ψ =1; 当采用矿场单位制时, χ =1.842, ψ =0.003 6。
1.2 地层流动模型
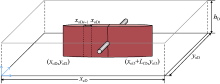
根据模型假设平台内多口水平井处于同一压力系统, 将地层内气体流动控制方程变量转化为拟压力、拟时间, 控制方程符合线性流动规律, 因此可以采用压力叠加原理解决缝间、井间的相互干扰问题。根据压力干扰效应可以将平台流动系统分解为以单裂缝为基本单元的子流动系统, 如图2所示。根据物质守恒原理, 气体拟压力控制方程满足：
\[\frac{{{\partial }^{2}}{{m}_{\text{m}}}}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}{{m}_{\text{m}}}}{\partial {{y}^{2}}}+\frac{{{\mu }_{\text{gi}}}{{B}_{\text{gi}}}}{{{K}_{\text{m}}}h}{{S}_{\text{f}}}(x, y, t)-\frac{{{\mu }_{\text{gi}}}}{{{K}_{\text{m}}}}{{q}_{\text{de}}}(t)= \frac{{{\phi }_{\text{m}}}{{\mu }_{\text{gi}}}{{c}_{\text{ti}}}}{{{K}_{\text{m}}}}\frac{\partial {{m}_{\text{m}}}}{\partial {{t}_{\text{a}}}}\ （16）\]
 | 图2 单裂缝引起的压力扰动示意图 |
其中, Sf(x, y, t)为水力裂缝内流动引起的扰动函数：
\[{{S}_{\text{f}}}=\int_{0}^{t}{\int_{{{x}_{\text{o}}}}^{{{x}_{\text{o}}}+{{L}_{\text{f}}}}{{{q}_{\text{f}}}(u, t-\tau )\delta (x-{{x}_{\text{o}}}-u, \tau )\delta (y-{{y}_{\text{o}}}, \tau )dud\tau }}\ （17）\]
考虑页岩解吸气影响时, qde(t)为解吸气的供给函数[7]：
\[{{q}_{\text{de}}}(t)=\frac{{{Z}_{\text{gi}}}{{p}_{\text{sc}}}T}{{{T}_{\text{sc}}}{{p}_{\text{i}}}}\frac{6{{D}_{\text{g}}}{{\pi }^{2}}}{R_{\text{m}}^{2}}({{V}_{\text{E}}}-V)\ （18）\]
将裂缝视为一个汇源中分布的连续函数\(\tilde{q}\)fd(s), 将额外气体供给处理为双孔介质模型f(s), 同时无因次化处理（16）式并进行Laplace时间变换, 可以得到无因次拟压力控制方程：
\[\frac{{{\partial }^{2}}{{{\tilde{p}}}_{\text{mD}}}}{\partial x_{\text{D}}^{2}}+\frac{{{\partial }^{2}}{{{\tilde{p}}}_{\text{mD}}}}{\partial y_{\text{D}}^{2}}+ \pi \int_{{{x}_{\text{oD}}}}^{{{x}_{\text{oD}}}+{{L}_{\text{fD}}}}{{{{\tilde{q}}}_{\text{fD}}}(s)\tilde{\delta }({{x}_{\text{D}}}-{{x}_{\text{oD}}}-{{u}_{\text{D}}})\tilde{\delta }({{y}_{\text{D}}}-{{y}_{\text{oD}}})d{{u}_{\text{D}}}}=sf(s){{\tilde{p}}_{\text{mD}}}\ （19）\]
从储集层角度看, 可以将裂缝进一步分解为N个带有不同流量强度的微元体, 同时假设每个微元体内流量分布均匀, 流量为qfDi且长度为\(\Delta {{x}_{fDi}}\)。根据压力叠加原理, 可以得到多裂缝在地层内任一点的压力：
\[{{\tilde{p}}_{\text{mD}}}({{x}_{\text{D}j}}, {{y}_{\text{D}j}})=\sum\limits_{i=1}^{N}{{{{\tilde{q}}}_{\text{D}i}}\tilde{p}_{\text{uD}j, i}^{{}}({{\beta }_{\text{D}j}}, {{\beta }_{\text{D}i}}, \text{ }\!\!\Delta\!\!\text{ }{{x}_{\text{fD}i}}, {{x}_{\text{eD}}}, {{y}_{\text{eD}}}, s)}\ （20）\]
其中\(\tilde{p}\)uDj, i代表第i个微元在第j个微元处引起的压力扰动, 利用Green函数和Newman乘积法[22], 同时结合Laplace变换, 计算裂缝微元段引起的不稳定压力分布：
\[{{\tilde{p}}_{\text{uD}j, i}}({{\beta }_{\text{wD}j}}, {{\beta }_{\text{wD}i}})=\frac{2\pi \text{ }\!\!\Delta\!\!\text{ }{{x}_{\text{fD}i}}}{{{x}_{\text{eD}}}}{{\tilde{H}}_{0}}+\ {{\tilde{F}}_{ji}}+ 4\sum\limits_{n=1}^{\infty }{\frac{{{{\tilde{H}}}_{n}}-1}{n{{\varepsilon }_{n}}}\cos \frac{n\pi {{x}_{\text{D}j}}}{{{x}_{\text{eD}}}}\sin \frac{n\pi {{x}_{\text{D}i}}}{{{x}_{\text{eD}}}}\cos \frac{n\pi \text{ }\!\!\Delta\!\!\text{ }{{x}_{\text{fD}i}}}{{{x}_{\text{eD}}}}}\ （21）\]
其中[7]
\[{{\tilde{H}}_{n}}=\frac{\cosh \left[ {{\varepsilon }_{n}}({{y}_{\text{eD}}}-|{{y}_{\text{D}j}}-{{y}_{\text{wD}i}}|) \right]}{\sinh ({{\varepsilon }_{n}}{{y}_{\text{eD}}})}\text{+}\frac{\cosh \left[ {{\varepsilon }_{n}}({{y}_{\text{eD}}}-|{{y}_{\text{D}j}}+{{y}_{\text{wD}i}}|) \right]}{\sinh ({{\varepsilon }_{n}}{{y}_{\text{eD}}})}\]
\[{{\tilde{F}}_{ji}}=\int_{-\text{ }\!\!\Delta\!\!\text{ }{{x}_{\text{fD}i}}}^{\text{ }\!\!\Delta\!\!\text{ }{{x}_{\text{fD}i}}}{\left( \frac{2\pi }{{{x}_{\text{eD}}}}\sum\limits_{n=1}^{\infty }{\frac{1}{{{\varepsilon }_{n}}}\cos \frac{n\pi {{x}_{\text{D}j}}}{{{x}_{\text{eD}}}}\cos \frac{n\pi {{u}_{\text{D}}}}{{{x}_{\text{eD}}}}} \right)d{{u}_{\text{D}}}}\]
\[{{\beta }_{\text{wD}j}}=({{x}_{\text{D}j}}, {{y}_{\text{D}j}})\] \[{{\varepsilon }_{n}}=\sqrt{sf(s)+{{n}^{2}}{{\pi }^{2}}/x_{\text{eD}}^{2}}\]
\[f(s)=\omega +\frac{{{a}_{\text{g}}}{{D}_{\text{D}}}(1-\omega )}{s+{{D}_{\text{D}}}}\]
由此可以获得沿着裂缝面的地层压力分布。为了便于计算, 将（20）式改写成矩阵形式：
\[\left( \begin{matrix} & {{{\tilde{p}}}_{\text{mD}1}} \\ & \ \ \vdots \\ & {{{\tilde{p}}}_{\text{mD}N}} \\ \end{matrix} \right)=\left( \begin{matrix} & \tilde{p}_{\text{uD}1, 1}^{{}}({{\beta }_{\text{wD}1}}, {{\beta }_{\text{wD}1}})\ \cdots \ \tilde{p}_{\text{uD}1, N}^{{}}({{\beta }_{\text{wD}1}}, {{\beta }_{\text{wD}N}}) \\ & \ \ \vdots \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots \ \ \ \ \ \ \ \ \ \ \ \\ & \tilde{p}_{\text{uD}N, 1}^{{}}({{\beta }_{\text{wD}N}}, {{\beta }_{\text{wD}1}})\ \cdots \ \tilde{p}_{\text{uD}N, N}^{{}}({{\beta }_{\text{wD}N}}, {{\beta }_{\text{wD}N}}) \\ \end{matrix} \right)\times \left( \begin{matrix} & {{{\tilde{q}}}_{\text{D}1}} \\ & \ \ \vdots \\ & {{{\tilde{q}}}_{\text{D}N}} \\ \end{matrix} \right)\ （22）\]
1.3 变导流裂缝流动模型
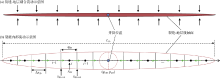
从裂缝角度看, 裂缝内的流动可视为有源汇的一维流动区域, 其中源指的是有流体不断从地层流入裂缝。单位长度裂缝流量（即流量密度）为qf(x, t); 在裂缝与井筒交汇处存在着汇, 流体从裂缝流入井筒, 裂缝流量为qw(t), 整个流动过程呈典型的变质量流（见图3a）。
 | 图3 裂缝内变质量流动示意图 |
本文建立了变缝宽的裂缝模型（见图3b）, 裂缝内的一维流动规律可使用如下无因次数学模型进行描述：
\[\frac{\partial }{\partial x_{\text{hfD}}^{{}}}\left[ {{C}_{\text{fD}}}(x_{\text{hfD}}^{{}})\frac{\partial {{{\tilde{p}}}_{\text{fD}}}}{\partial x_{\text{hfD}}^{{}}} \right]-2\pi {{\tilde{q}}_{\text{fD}}}({{x}_{\text{hfD}}})+ 2\pi \left[ {{{\tilde{q}}}_{\text{wD}}}({{t}_{\text{D}}})\delta ({{x}_{\text{hfD}}}, {{x}_{\text{whfD}}}) \right]=0\ （23）\]
其中, δ 为Dirac函数, 无因次变导流能力函数为：
\[{{C}_{\text{fD}}}({{x}_{\text{hfD}}})={{C}_{\text{fDmax}}}(-x_{\text{hfD}}^{2}+2{{x}_{\text{hfD}}})\ （24）\]
（23）式为非常系数线性微分方程, 无法直接求解, 引入坐标变换法对其进行常系数化处理。坐标转换方程如下：
\[{{\xi }_{\text{D}}}({{x}_{\text{hfD}}})={{\hat{C}}_{\text{fD}}}\int_{0}^{{{x}_{\text{hfD}}}}{C_{\text{fD}}^{-1}\left[ {{p}_{\text{fD}}}({{x}_{\text{D}}}) \right]d{{x}_{\text{D}}}}\ （25）\]
其中 \[{{\hat{C}}_{\text{fD}}}=\frac{{{L}_{\text{fD}}}}{\int_{0}^{{{L}_{\text{fD}}}}{C_{\text{fD}}^{-1}\left[ {{p}_{\text{fD}}}({{x}_{\text{D}}}) \right]d{{x}_{\text{D}}}}}\]
使用（25）式对（23）式进行处理, 可以在新坐标下获得常系数线性微分方程, 在此基础上使用边界元方法进行双重积分处理[23], 得到裂缝内的无因次压力分布：
\[\tilde{p}_{\text{wD}}^{{}}-\tilde{p}_{\text{fD}}^{{}}({{\xi }_{\text{D}}})=\frac{2\pi }{{{{\hat{C}}}_{\text{fD}}}}{{\tilde{q}}_{\text{wD}}}G({{\xi }_{\text{D}}}, {{\xi }_{\text{wD}}})-\frac{2\pi }{{{{\hat{C}}}_{\text{fD}}}}\left[ I({{\xi }_{\text{D}}})-I({{\xi }_{\text{wD}}}) \right]\ （26）\]
其中, G为Heaviside阶跃函数的积分函数, Fredholm积分式为：
\[I({{\xi }_{\text{D}}})=\int_{0}^{{{\xi }_{\text{D}}}}{d\zeta \int_{0}^{\zeta }{{{{\tilde{q}}}_{\text{fD}}}(\varsigma )d\varsigma }}\ （27）\]
考虑到裂缝与井筒相交点周围的聚流效应, 引入聚流表皮因子Sc[24], 修正裂缝内压力降：
\[\tilde{p}_{\text{wD}}^{{}}-\tilde{p}_{\text{fD}}^{{}}({{\xi }_{\text{D}}})=\frac{2\pi }{{{{\hat{C}}}_{\text{fD}}}}{{\tilde{q}}_{\text{wD}}}G({{\xi }_{\text{D}}}, {{\xi }_{\text{wD}}})-\frac{2\pi }{{{{\hat{C}}}_{\text{fD}}}}\left[ I({{\xi }_{\text{D}}})-I({{\xi }_{\text{wD}}}) \right]+{{\tilde{q}}_{\text{wD}}}{{S}_{\text{c}}}\ （28）\]
其中 \({{S}_{\text{c}}}=\frac{2{{h}_{\text{D}}}}{{{{\hat{C}}}_{\text{fD}}}{{L}_{\text{fD}}}}\left[ \ln \left( \frac{{{h}_{\text{D}}}}{2{{r}_{\text{wD}}}} \right)-\frac{\pi }{2} \right]\)
同样地, 可以将（28）式改写为矩阵形式：
\[\left(\begin{matrix} & {{{\tilde{p}}}_{\text{wD}}} \\ & \vdots \\ & {{{\tilde{p}}}_{\text{wD}}} \\ \end{matrix} \right)-\left(\begin{matrix} & {{{\tilde{p}}}_{\text{fD}1}} \\ & \vdots \\ & {{{\tilde{p}}}_{\text{fD}N}} \\ \end{matrix} \right)=\frac{2\pi }{{{{\hat{C}}}_{\text{fD}}}}\left(\begin{matrix} & {{{\tilde{q}}}_{\text{wD}}}{{\gamma }_{1}} \\ & \vdots \\ & {{{\tilde{q}}}_{\text{wD}}}{{\gamma }_{N}} \\ \end{matrix} \right)- \\ \frac{2\pi }{{{{\hat{C}}}_{\text{fD}}}}\left(\begin{matrix} & \alpha _{1, 1}^{{}}\ \ \ \cdots \ \ \alpha _{1, N}^{{}} \\ & \vdots \ \ \ \ \ \ \ \ \ \vdots \ \\ & \alpha _{N, 1}^{{}}\ \ \cdots \ \ \alpha _{N, N}^{{}} \\ \end{matrix} \right)\times \left(\begin{matrix} & {{{\tilde{q}}}_{\text{fD}1}} \\ & \vdots \\ & {{{\tilde{q}}}_{\text{fD}N}} \\ \end{matrix} \right)+{{S}_{\text{c}}}\left(\begin{matrix} & {{{\tilde{q}}}_{\text{wD}}} \\ & \vdots \\ & {{{\tilde{q}}}_{\text{wD}}} \\ \end{matrix} \right)\ （29）\]
其中 \[{{\gamma }_{i}}=G({{\xi }_{Di}}, {{\xi }_{wD}})\] \[{{\alpha }_{j, i}}=R{{S}_{i}}+R{{T}_{i}}\]
\[G(x, {{x}_{0}})=\left\{ \begin{align} & x-{{x}_{0}}\ \ (x\ge {{x}_{0}}) \\ & 0\ \, \ (x< {{x}_{0}}) \\ \end{align} \right.\]
\[R{{S}_{i}}=\left\{ \begin{align} & {{\xi }_{\text{D}j}}\text{ }\!\!\Delta\!\!\text{ }{{\xi }_{\text{D}j}}-0.5(\xi _{\text{oD, }i}^{2}-\xi _{\text{oD, }i-1}^{2})\quad (i< j) \\ & {{\xi }_{\text{D}j}}({{\xi }_{\text{D}j}}-{{\xi }_{\text{oD, }j-1}})-0.5(\xi _{\text{D}j}^{2}-\xi _{\text{oD, }j-1}^{2})\quad \ (i=j) \\ \end{align} \right.\]
\[R{{T}_{i}}=\left\{ \begin{align} & ({{\xi }_{\text{wD}}}-{{\xi }_{\text{D}i}})\text{ }\!\!\Delta\!\!\text{ }{{\xi }_{\text{D}j}}\quad (i< 1+\Xi \text{)} \\ & \left( {{\xi }_{\text{wD}}}-\sum\limits_{i=1}^{\Xi }{\text{ }\!\!\Delta\!\!\text{ }{{\xi }_{\text{D}i}}} \right)\left( 0.5{{\xi }_{\text{wD}}}+\sum\limits_{i=1}^{\Xi }{\text{ }\!\!\Delta\!\!\text{ }{{\xi }_{\text{D}i}}} \right)\quad (i=1+\Xi ) \\ \end{align} \right.\]
2 模型求解及验证
地层流动模型与裂缝流动模型在裂缝面进行流量、压力耦合, 满足如下公式：
\[\left\{ \begin{align} & {{{\tilde{p}}}_{\text{fD}}}({{x}_{\text{hfD}}})={{{\tilde{p}}}_{\text{mD}}}({{x}_{\text{oD}}}+{{x}_{\text{hfD}}}, {{y}_{\text{oD}}}) \\ & {{{\tilde{q}}}_{\text{fD}}}={{{\tilde{q}}}_{\text{mD}}} \\ \end{align} \right.\ （30）\]
值得注意的是, 经过坐标转换后的无因次裂缝流量qwD与无因次裂缝流量密度qfDj的关系为：
\[{{\tilde{q}}_{\text{wD}}}=\sum\limits_{j=1}^{N}{{{{\tilde{q}}}_{\text{fD}j}}{{f}_{\text{c}j}}} \ （31）\]
其中\({{f}_{\text{c}j}}=\Delta {{\xi }_{\text{D}j}}/\Delta {{x}_{\text{D}j}}\)那么（22）式中矩阵元素\(\tilde{p}_{\text{uD}j, i}^{{}}({{\beta }_{\text{wD}j}}, {{\beta }_{\text{wD}i}})\)修正为\({{f}_{\text{c}j}}\tilde{p}_{\text{uD}j, i}^{{}}({{\beta }_{\text{wD}j}}, {{\beta }_{\text{wD}i}})\)。
利用压降叠加原理, 将多井平台渗流系统分解为多个单级裂缝, 以单裂缝为基本评价单元。针对单条裂缝联立（22）式和（29）式辅以相应的耦合条件（30）— （31）式, 通过求解耦合矩阵可以计算沿裂缝的流量分布, 进而计算产量, 同时根据累计产量与产量在Laplace空间下的转换关系（\(\tilde{G}\)pD=\(\tilde{q}\)wD/s）获得累计产量。上述求解方程中的未知量可表述为如下矩阵：
\[{{X}^{T}}= \begin{align} & \left( \tilde{q}_{\text{fD}1, 1}^{\quad \left\langle 1 \right\rangle }, \tilde{q}_{\text{fD}1, 2}^{\quad \left\langle 1 \right\rangle }, \cdots , \tilde{q}_{\text{fD}1, N}^{\quad \left\langle 1 \right\rangle }, \ldots , \tilde{q}_{\text{fD}{{n}_{f}}, 1}^{\quad \left\langle 1 \right\rangle }, \tilde{q}_{\text{fD}{{n}_{f}}, 2}^{\quad \left\langle 1 \right\rangle }, \ldots , \tilde{q}_{\text{fD}{{n}_{f}}, N}^{\quad \ \ \ \left\langle 1 \right\rangle }, \tilde{q}_{\text{wD}}^{\ \, \left\langle 1 \right\rangle }, \tilde{G}_{\text{pD}}^{\ \ \left\langle 1 \right\rangle }, \ldots , \right. \\ & \left. \tilde{q}_{\text{fD}1, 1}^{\ \left\langle {{n}_{w}} \right\rangle }, \tilde{q}_{\text{fD}1, 2}^{\ \left\langle {{n}_{w}} \right\rangle }, \cdots , \tilde{q}_{\text{fD}1, N}^{\quad \left\langle {{n}_{w}} \right\rangle }, \ldots , \tilde{q}_{\text{fD}{{n}_{f}}, 1}^{\quad \left\langle {{n}_{w}} \right\rangle }, \tilde{q}_{\text{fD}{{n}_{f}}, 2}^{\quad \left\langle {{n}_{w}} \right\rangle }, \ldots , \tilde{q}_{\text{fD}{{n}_{f}}, N}^{\left\langle {{n}_{w}} \right\rangle }, \tilde{q}_{\text{wD}}^{\left\langle {{n}_{w}} \right\rangle }, \tilde{G}_{\text{pD}}^{\left\langle {{n}_{w}} \right\rangle } \right) \\ \end{align}\ （32）\]
需要指明的是, 拟时间是关于时间和空间的积分函数, 可将拟时间近似处理为平均地层压力关于时间的单重积分函数, 如（33）式所示, 结合物质平衡（34）式进行计算, 具体算法可参考文献[25]。
\[{{t}_{\text{a}}}=t\ {{\beta }_{\text{m}}}\left[ {{p}_{\text{avg}}}\left( t \right) \right]\ （33）\]
\[\frac{{{p}_{\text{avg}}}(t)}{{{Z}_{\text{avg}}}(t)}=\frac{{{p}_{\text{i}}}}{{{Z}_{\text{i}}}}\left( 1-\frac{{{G}_{\text{p}}}}{OGIP} \right)\ （34）\]
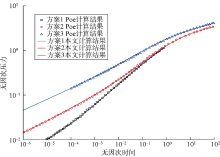
.分别使用解析模型和数值模型验证模型的可靠性。Poe等将裂缝单翼分成4个不同的流动区域, 建立了非均质裂缝定产量模型, 并.获得了经典无因次压力图版[26]。本文将聚流表皮因子去除后计算定产量条件下的无因次压力, 计算结果与Poe图版的3个方案分别进行对比。如图4所示, 2种模型计算结果完全一致, 从而验证了本文算法在单条变缝宽裂缝压力动态模拟条件下的适用性。
 | 图4 非均质导流能力垂直裂缝无因次压力对比 |
为进一步验证, 借助Eclipse数值模拟器建立多口分段压裂水平井模型。模型参数如下：原始地层压力45.0 MPa, 井底压力6.5 MPa, 有效裂缝高度20 m, 地层有效孔隙度8%, 含油饱和度85%, 综合压缩系数4.35× 10-4 MPa-1, 有效泄流区域内地层平均渗透率0.01× 10-3 μ m2, 井底压力6.5 MPa。原油黏度1 mPa· s, 体积系数1.0 m3/m3, 井筒半径0.019 m。裂缝段数为30, 地层几何尺寸为1 500 m× 1 600 m× 20 m, 裂缝有效半长114.95 m, 裂缝宽度为0.012 7 m, 孔隙度为35%。为精确模拟生产动态, 裂缝采用网格对数加密描述, 在裂缝导流能力相同的条件下, 数值模型中裂缝等效宽度0.1 m, 等效孔隙度为4.4%, 等效裂缝最大渗透率采用公式Kfmax=12CfD计算, 在本文算例中分别为37.68× 10-3, 376.8× 10-3, 3 768× 10-3 μ m2, 沿裂缝渗透率分布如图5所示。
 | 图5 沿主裂缝渗透率分布 |
由于采用均匀布井, 3口井压力分布一致。对比本文算法与数值模拟获得的无因次生产动态数据（见图6）, 结果表明2种算法获得的单井产量与累计产量高度吻合, 进一步验证了本文算法在多井、多裂缝条件下的适用性。
 | 图6 2种算法计算得到的无因次产量及累计产量对比 |
3 裂缝与井距参数优化
影响开发平台生产动态的主要因素包括裂缝数、裂缝长度、导流能力、水平井数、压裂段长度以及相应的位置分布等。由于影响因素较多, 为便于讨论, 把握主要因素间的内在关联, 本文假设一种理想模式, 即裂缝与水平井均匀分布, 缝与缝、井与井之间参数一致。具有相同属性的裂缝占相同的子泄流面积（子泄流面积为总泄流面积的1/（nwnf））, 这样影响多井平台生产特征的因素可归结为两大类：裂缝总长度和裂缝导流能力。
在给定支撑剂量条件下裂缝总长度和裂缝导流能力增加会共同“ 争夺” 支撑剂体积, 当两者间达到平衡状态时, 生产井产能指数达到最大, 即Economides等提出的支撑剂指数法, 传统支撑剂指数法理论仅适用于单条均匀导流裂缝的拟稳态假设条件, 以拟稳态产能指数为优化目标, 与时间无关[27, 28]。
本文以多井系统为研究对象, 以总支撑剂体积（与压裂规模相关）为约束条件, 以动态累计产量为优化目标, 建立全生命周期的压裂-水平井参数动态优化方法。其中, 改进的支撑剂指数定义为：
\[{{N}_{\text{prop}}}=\frac{4{{x}_{\text{ef}}}}{3{{y}_{\text{ef}}}}\frac{{{n}_{\text{f}}}{{C}_{\text{fDmax}}}I_{\text{x}}^{2}}{{{n}_{\text{w}}}}\ （35）\]
为方便标记, 下文中提及的无因次导流能力即为（35）式中的CfDmax。
3.1 裂缝导流能力和长度优化
裂缝导流能力和裂缝长度是平衡裂缝与地层流入流出关系的关键指标（本文假设裂缝高度与地层厚度相等）, 考虑到裂缝宽度与裂缝渗透率之间呈正相关关系, 使用裂缝导流能力（Kfwf）代替裂缝宽度。本文以单裂缝为研究对象, 聚焦裂缝导流能力和长度优化过程, 地层尺寸假设为400 m× 50 m× 20 m, 使用裂缝穿透率表征裂缝长度（Ix=Lf/xe）, 无因次导流能力表征裂缝导流能力。
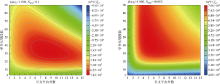
裂缝导流能力和长度随支撑剂指数变化的优化结果如图7所示, 当压裂规模不考虑支撑剂体积约束时, 无因次累计产量随裂缝穿透比和导流能力增加而单调递增, 但递增幅度逐渐减小, 直到极限值, 此时裂缝完全贯穿地层且达到无限导流能力; 而考虑约束时, 累计产量与裂缝导流能力和长度存在最优值, 即图中离散点, 最大无因次累计产量随着支撑剂指数增加而增加。对比图7a和图7b可以看出, 不同时刻下最优裂缝导流能力和长度结果不同。
 | 图7 不同时刻有限导流裂缝导流能力和长度优化 |
为厘清生产时间对优化结果的影响, 重新计算获得裂缝导流能力随时间变化的优化结果（见图8）。以图8a为例, 最大无因次累计产量随着生产时间增加而增加, 而最优裂缝无因次导流能力却逐渐递减且趋近于常数。对比图8a— 8d可以看出, 支撑剂指数越大, 在相同时刻下所对应的最大无因次累计产量越大, 在相同时间间隔内最优无因次导流能力值的变化区间越大, 且所趋近的常数也越大。图8b在无因次时间为0.01~1 000时对应的最优无因次导流能力为1.62~100.00, 趋近值为1.62; 图8d在相同的时间间隔内最优无因次导流能力为15~400, 趋近于15。
 | 图8 不同支撑剂指数下的有限导流裂缝导流能力动态优化图版 |
图9总结了不同时刻、不同支撑剂指数下的最优裂缝导流能力和长度、最大累计产量的变化规律。图9a表明当支撑剂指数较小时, 随着支撑剂指数的减小最优无因次导流能力逐渐递减且趋近于常量; 无因次时间越大, 最优无因次导流能力维持常量所对应的支撑剂指数区间越大, 如无因次时间为1 000时最优无因次导流能力在支撑剂指数为1× 10-8~1× 10-1时均为常量, 无因次时间为0.01时最优无因次导流能力在支撑剂指数为1× 10-8~1× 10-7时为常量。随着支撑剂指数增加, 最优无因次导流能力和最优裂缝穿透比均增加, 当裂缝完全贯穿地层时（Ix=1）, 最优无因次导流能力与支撑剂指数呈线性关系。图9b表明当支撑剂指数一定时, 随着生产时间的增加, 最优无因次导流能力不断减小且趋近于常量, 常量值与支撑剂指数呈正相关关系, 如支撑剂指数为1× 10-2时对应最优无因次导流能力为1.62, 支撑剂指数为1× 103时对应最优无因次导流能力为175。总的来看, 当无因次生产时间（即生产周期）较短时, 可压裂长度较小且导流能力较高的裂缝; 当无因次生产时间较长时, 可压裂长度较大且导流能力较低的裂缝。需要强调的是, 最优无因次导流能力所趋近特征值1.62与Valko和Economides优化结果基本一致[27], 也证明了本文优化方法的可靠性。
 | 图9 生产时间和支撑剂指数对裂缝导流能力和长度优化的影响 |
3.2 缝距-井距优化
在泄流面积不变的条件下, 裂缝泄流面积形状会影响裂缝导流能力和长度的优化结果, 本文使用缝距与井距比值（λ =ye/xe）表征泄流面积形状, 该值由裂缝数和水平井数确定（ye=yef/nf, xe=xef/nw）。图10反映了λ 值对裂缝生产动态的影响, 其中假设裂缝为完全贯穿、无限导流。当产量递减至近似为0时无因次累计产量趋近于极限值（0.5xeDyeD/π ）, 由于泄流面积相等, 不同λ 值下的极限累计产量相同。当λ 值较小时, 对应泄流面积呈长条状, 裂缝与地层接触面积较大, 渗流阻力较小, 裂缝早期产量较高, 能在较短时间内达到极限累计产量。同时, λ 较小时所对应的无因次累计产量在整个生产周期内始终高于λ 较大时。
 | 图10 缝距与井距比值对生产动态特征的影响图版 |
考虑支撑剂指数约束后, λ 值对最大无因次累计产量及最优裂缝导流能力和长度均会产生影响（见图11）。如图11a所示, 随着支撑剂指数的增加最大无因次累计产量趋近于最高值, λ 值越小（窄缝距、大井距模式）对应的最高值越大, 此时裂缝达到无限导流能力且完全贯穿地层（见图11b）。当支撑剂指数较小时（小于1× 103）, 不同λ 值对应的最优无因次导流能力相同, 但较大λ 值对应的最优裂缝穿透比较大（见图11b）, 所以相应的最大无因次累计产量较大（见图11a）。需要强调的是, 图版所反映的特征与生产时间取值有关, 当时间足够大时所有λ 值对应的无因次最大累计产量均相等, 而当时间足够小时在低支撑剂指数下λ 值对图版的影响很小。
 | 图11 缝距与井距比值对裂缝导流能力和长度优化的影响（tD=1 000） |
3.3 多参数系统优化
优化多井平台压裂水平井的开发效果主要通过增加裂缝与地层接触面积、降低井间干扰和缝间干扰、平衡裂缝与地层的流入流出关系实现, 当这几种关系达到平衡时生产效果最佳。
本文假定半支平台几何尺寸为1 500 m× 1 500 m× 20 m, 以支撑剂体积为约束条件, 以总NPV值（净现值）为目标函数, 采用嵌套式方法进行多参数优化。优化流程主要分为以下步骤：①定义输入基本参量, 包括地层参数、流体参数、支撑剂参数和生产周期; ②定义3种待优化变量, 包括平台内井数、单井压裂段数和支撑剂体积; ③根据前文所述支撑剂指数法计算不同井数、压裂段数和支撑剂体积条件下的最优裂缝导流能力和长度及对应的最大累计产量; ④计算相应的NPV值; ⑤基于多元函数Powell全局优化算法重复步骤②, 直到NPV值最大, 此时对应的水平井-压裂参数即为最优设计参数。其中, NPV计算模型为[16]：
\[\begin{align} & NPV=\sum\limits_{ii=1}^{{{n}_{year}}}{\frac{({{G}_{\text{p}, ii}}-{{G}_{\text{p}, ii-1}}){{P}_{\text{gas}}}}{{{(1+{{i}_{r}})}^{ii}}}}- \\ & \ \ \ \ \ \ \ \ \ \ \left[ FC+\sum\limits_{k=1}^{{{n}_{\text{w}}}}{({{C}_{\text{well}}}+\sum\limits_{k=1}^{{{n}_{\text{f}}}}{{{C}_{\text{fracture}}}})} \right] \\ \end{align}\ （36）\]
本文设定无因次时间1 000为生产周期, 考虑到实际压裂规模受工程条件限制, 将平台总支撑剂体积设定为固定的约束条件, 使用图解法说明多参数优化流程。
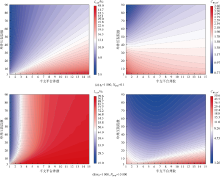
图12为不同水平井数、不同单井压裂段数下的平台最大累计产量。由图12可知, 平台最大累计产量随井数和单井压裂段数的增加而单调增加, 当支撑剂指数较小时平台最大累计产量随井数和段数的增加幅度基本一致（见图12a）; 当支撑剂指数较大时平台最大累计产量增加幅度相对减小, 在单井压裂段数大于30、平台井数大于5的区域内平台最大累计产量几乎不再增加（见图12b）。因此, 以平台最大累计产量为目标函数、压裂规模为约束条件的情况下, 平台内部仅存在最优裂缝导流能力和长度, 但不存在最优井距（井数）、缝距（缝数）。
将开发指标计算结果代入经济评价模型, 以NPV为目标函数重新进行优化, 结果如图13所示。图13中出现了明显的极值点, 说明存在最优井距、缝距。同样地, 对应的裂缝导流能力和长度优化结果如图14所示。随着压裂段数和井数的增加, 虽然提高了平台的开发效果, 但投资成本随之增加, 当开发效果增加幅度小于投资增长幅度时经济效益变差。因此在压裂规模和经济效益双重约束下多井平台内存在最优井距、缝距及裂缝导流能力和长度, 这为开发技术政策的制定提供了优化空间。
由图13和图14看出, 在本文算例中, 当压裂规模较小时（Nprop=0.1）, 最优井距较小（nw, opt≈ 8）、最优缝距较宽（nf, opt≈ 35）, 裂缝穿透率较小（Ix, opt≈ 11%）、裂缝导流能力较低（CfD, opt≈ 1.60）。当压裂规模较大时（Nprop=1× 104）, 相比于小规模压裂情况, 最优井距增加（nw, opt≈ 6）、最优缝距减小（nf, opt≈ 50）, 裂缝穿透率大幅度提高（Ix, opt≈ 72%）, 但裂缝导流能力仍处于较低水平（CfD, opt≈ 3.54）。
开发平台水平井-压裂参数优化结果与设定的参数条件相关, 如平台几何尺寸、开发评价周期、经济参数、裂缝形态复杂程度以及压裂规模约束类型（固定单缝、单井或平台支撑剂体积）等。
 | 图12 不同支撑剂指数条件下半支平台最大无因次累计产量值 |
 | 图13 不同支撑剂指数条件下半支平台最大NPV值 |
 | 图14 多井平台下的裂缝导流能力和长度优化图版 |
4 结论
针对开发平台内多口存在变缝宽裂缝的水平井, 利用压力叠加原理, 给出了一种新的变导流裂缝与储集层耦合流动的半解析模型。通过坐标变换将变导流裂缝转换为常导流裂缝, 可以处理空间位置及导流能力分布复杂的裂缝流动, 并给出灵活的地层-裂缝耦合流动矩阵, 方便模型快速求解。
考虑压裂规模约束时以累计产量为目标函数, 存在最佳裂缝导流能力和长度, 随着支撑剂指数和生产时间增加最大累计产量增加, 最优裂缝穿透比增加; 随着支撑剂指数减小、生产时间增加, 最优无因次导流能力值不断减小且趋近于经典特征值（1.62）。缝距与井距比值也将影响裂缝导流能力和长度的优化结果, 在高支撑剂指数情况下, 大井距、窄缝距的部署模式更具优势。
当不考虑经济效益时, 开发平台的生产效果随着单井裂缝数、水平井数的增加而增加, 不存在最优井数、段数, 增加幅度随着支撑剂指数的增加而降低, 当井数与单井压裂段数同时超过特定值时, 平台累计产量几乎不再增加。
以净现值为优化目标函数, 累计产量提高导致的正现金流与井数、段数增加产生的负现金流相互冲抵, 出现参数优化空间, 存在最优裂缝导流能力、裂缝长度、井数、段数, 在压裂规模较小情况下宜采用小井距、宽缝距、短裂缝的水平井部署模式; 在压裂规模较大情况下则宜采用大井距、窄缝距、长裂缝的部署模式。
符号注释：
ag— — 气体解吸系数, 无因次; Bg— — 气体体积系数, m3/m3; bam— — 滑脱因子, 无因次; CfD— — 无因次导流能力; Cfracture— — 单段裂缝压裂成本, 元; Cwell— — 单井钻井成本, 元; cg— — 气体压缩系数, Pa-1; ct— — 地层压缩系数, Pa-1; DD— — 无因次扩散系数; Dg— — 基质扩散系数, m2/s; FC— — 固定总投资, 元; Gp— — 累计产量, m3; Gp, ii— — 第ii年累计产量, m3; h— — 地层厚度, m; Ix— — 裂缝穿透比, %; ii— — 年份编号; ir— — 年利率; Kf— — 裂缝渗透率, m2; Km— — 地层渗透率, m2; Lf— — 裂缝全长, m; Lref— — 参考长度, m; mf— — 裂缝内拟压力, Pa; mm— — 基质内拟压力, Pa; N— — 裂缝微元段个数; Nprop— — 支撑剂指数; NPV— — 净现值, 元; n— — 无穷级数计数符号; nf— — 单井裂缝数; nw— — 开发平台内井数; nyear— — 生产年限, a; OGIP— — 原始地质储量, m3; Pgas— — 气价, 元/m3; p— — 压力, Pa; pf— — 裂缝内压力, Pa; pm— — 地层压力, Pa; pm— — 压力梯度, Pa/m; pw— — 井筒处压力, Pa; pwf— — 井底压力, Pa; qf— — 裂缝流量密度, m2/s; qm— — 地层流量密度, m2/s; qw— — 瞬时产量, m3/s;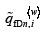 
（编辑 刘恋）
The authors have declared that no competing interests exist.
参考文献
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|