引用本文
刘修善. 井眼轨迹不确定性表征方法[J]. 石油勘探与开发, 2019,46(2): 391-396.
LIU Xiushan. Borehole trajectory uncertainty and its characterization[J]. Petroleum Exploration & Development, 2019,46(2): 391-396.  
Doi: 10.11698/PED.2019.02.20
Permissions
Copyright©2019, 《石油勘探与开发》编辑部
《石油勘探与开发》编辑部 所有
井眼轨迹不确定性表征方法
刘修善
中国石化石油工程技术研究院,北京100101

第一作者简介：刘修善（1962-）,男,黑龙江牡丹江人,博士,中国石化石油工程技术研究院教授级高级工程师,主要从事导向钻井工艺、井下信息测量与控制等方面的研究工作。地址：北京市朝阳区北辰东路8号北辰时代大厦9层,中国石化石油工程技术研究院,邮政编码：100101。E-mail：liuxs.sripe@sinopec.com

收稿日期: 2018-08-13
基金项目: 国家科技重大专项“海相碳酸盐岩超深油气井关键工程技术”（2017ZX05005-005）
摘要

针对井眼轨迹的不确定性问题提出了误差椭球姿态表征、截面误差椭圆解算、误差椭圆柱构建等方法,并进行实例计算。根据井斜角、方位角和工具面角定义,提出了井眼轨迹误差椭球姿态的表征方法;通过空间任意平面截取误差椭球,建立了截面误差椭圆的通用概念及算法,以分析井眼轨迹在水平面、铅垂面、法平面等任意平面上的误差;基于曲面相切和曲线投影理论,提出了井眼轨迹误差椭圆柱的构建方法,可评价井眼轨迹的轴向包络误差及其沿井深的变化情况。研究表明,井越深井眼轨迹误差越大;在使用常规随钻测量的深井超深井中,井眼轨迹位置误差可达数十米。提供了成套的井眼轨迹误差分析方法,用于评价井眼轨迹的监测精度及可靠性。图3表3参14

关键词: 钻井理论; 定向钻井; 井眼轨迹; 随钻测量; 不确定性; 误差分析
中图分类号:TE21 文献标志码:A 文章编号:1000-0747(2019)02-0391-06
Borehole trajectory uncertainty and its characterization
LIU Xiushan
Sinopec Research Institute of Petroleum Engineering, Beijing 100101, China
Abstract

To solve the problem of borehole trajectory uncertainty, some methods such as error ellipsoid posture characterization, sectional error ellipse solution and error elliptic cylinder construction were proposed and an application example was given. According to the definition of inclination, azimuth and tool-face angle, a characterization method of error ellipsoid posture of borehole trajectory was presented. By intercepting the error ellipsoid with an arbitrary plane in space, the general concept and algorithm of sectional error ellipse were established to analyze the borehole trajectory errors in horizontal plane, plumb plane, normal plane, etc. Based on the theory of surface tangency and curve projection, a construction method of error elliptic cylinder of borehole trajectory was put forward to evaluate the axial enveloping error of borehole trajectory and its variation along well depth. The research shows that the deeper the well, the greater the borehole trajectory error will be. In deep and ultra-deep wells measured using conventional measurement while drilling (MWD), the borehole trajectory position error reaches tens of meters. The research results provide a complete set of analysis methods for borehole trajectory error, which can evaluate the accuracy and reliability of borehole trajectory monitoring.

Keyword: drilling theory; directional drilling; borehole trajectory; measurement-while-drilling; uncertainty analysis; error analysis
0 引言

井眼轨迹设计、监测与控制的基本目标是定位井眼轨迹的空间位置。然而, 由于存在测量、计算等误差, 井眼轨迹定位不可能绝对准确。通过误差校正等途径能提高井眼轨迹定位精度, 但是却无法完全消除误差, 因此井眼轨迹存在不确定性问题。特别是密集井网、薄油层等油气田开发和海上平台、救援井等钻井作业更需要定量表征井眼轨迹的不确定性, 以降低钻井作业风险并提高油气田开发效果[1]。

为规范井眼轨迹不确定性的评价方法, 国际石油工程师协会（SPE）成立了专门的行业指导委员会（Industry Steering Committee for Wellbore Survey Accuracy, 简称ISCWSA）, 建立了ISCWSA井眼轨迹误差模型, 并随时更新和维护误差源及误差模型[2, 3, 4, 5, 6, 7, 8, 9, 10]。相比Wolff and De Wardt、SESTEM等模型[10, 11], ISCWSA模型被公认为是国际性行业标准。

基于井眼轨迹误差模型可以得到各测点处的协方差矩阵, 用以描述井眼轨迹空间位置的不确定性, 但是ISCWSA不提供井眼轨迹误差椭球的表征方法。虽然用椭球主轴与参考系坐标轴的夹角能表征误差椭球的空间姿态[12], 但是不符合行业习惯且使用不便。此外, 还有用水平面截取误差椭球以分析水平面上的井眼轨迹误差的研究成果[13, 14]。

为满足涉及井眼轨迹误差分析的各种工程需求, 本文提出了误差椭球姿态表征、截面误差椭圆解算、误差椭圆柱构建等方法, 用以分析井眼轨迹在空间任意平面上的误差和轴向包络误差及其沿井深变化情况, 具有清晰的物理和工程意义。

1 误差传播与集成模型

误差源是井眼轨迹误差分析的基本要素, ISCWSA已识别出80多个误差源[10], 常见误差源包括传感器误差、BHA（井下钻具组合）轴向及周向磁干扰、BHA下坠及工具组件径向不对称引起的不对中误差、地磁场不确定性、井深误差等。井眼轨迹误差模型主要考虑具有代表性的不确定性因素, 不包括偶然事件、测斜仪缺陷、录入数据有误等过失误差。误差模型的假设条件为[2, 3, 4, 5, 6, 7, 8, 9, 10]：①只考虑测量误差引起的井眼轨迹位置误差; ②每个测点可用井深、井斜角和方位角来表征; ③不同误差源的误差在统计学上相互独立; ④测量误差大小与相应井眼轨迹位置变化为线性关系; ⑤各种测量误差对井眼轨迹位置的综合影响等于各自影响的向量和。

为表征误差源对井眼轨迹位置误差的影响规律, Brooks和Wilson建立了误差传播方程[2, 3, 4, 5]：

${{\mathbf{e}}_{h}}={{\sigma }_{h}}\frac{d\mathbf{r}}{d\mathbf{p}}\frac{\partial \mathbf{p}}{\partial {{\varepsilon }_{h}}}$ （1）

其中 $\frac{\partial \mathbf{p}}{\partial {{\varepsilon }_{h}}}\text{=}{{\left[ \begin{matrix}\frac{\partial L}{\partial {{\varepsilon }_{h}}}, & \frac{\partial \alpha }{\partial {{\varepsilon }_{h}}}, & \frac{\partial \phi }{\partial {{\varepsilon }_{h}}} \\\end{matrix} \right]}^{T}}$

$\frac{d\mathbf{r}}{d\mathbf{p}}\text{=}\left[ \begin{matrix}\frac{dN}{dL} & \frac{dN}{d\alpha } & \frac{dN}{d\phi } \\\frac{dE}{dL} & \frac{dE}{d\alpha } & \frac{dE}{d\phi } \\\frac{dH}{dL} & \frac{dH}{d\alpha } & \frac{dH}{d\phi } \\\end{matrix} \right]$

为表征不同测点、多次测量以及不同井之间的误差相关性和累积效果, ISCWSA将误差传播模式分为随机误差、系统误差、单井误差和全局误差, 并定义了相关系数。据此, 任一测点K处的误差累计结果可表示为：

${{C}_{K}}=\sum\limits_{h\in Rand}{C_{h, K}^{{}}}+\sum\limits_{h\in Syst}{C_{h, K}^{{}}}+\sum\limits_{h\in \left\{ Well, Glob \right\}}{C_{h, K}^{{}}}$ （2）

ISCWSA提供了不同误差传播模式下的协方差矩阵计算方法[2, 3, 4, 5, 6, 7, 8, 9, 10], 所以在每个测点处都可得到3× 3协方差矩阵CK, 其中井口坐标系O-NEH下的协方差矩阵可表示为：

${{C}_{NEH}}=\left[ \begin{matrix}\sigma _{N}^{2} & {{\sigma }_{NE}} & {{\sigma }_{NH}} \\{{\sigma }_{NE}} & \sigma _{E}^{2} & {{\sigma }_{EH}} \\{{\sigma }_{NH}} & {{\sigma }_{EH}} & \sigma _{H}^{2} \\\end{matrix} \right]$ （3）

2 误差椭球及姿态表征

假设井眼轨迹的位置误差服从正态分布, 则误差分布的等概率密度面为[2, 3, 4, 5]：

${{\left( \delta \mathbf{r} \right)}^{T}}C_{NEH}^{-1}\left( \delta \mathbf{r} \right)={{k}^{2}}$ （4）

其中 $\delta \mathbf{r}={{\left[ \begin{matrix}\delta N, & \delta E, & \delta H \\\end{matrix} \right]}^{T}}$

这是关于放大系数k的椭球族, 给定1个k值就确定1个椭球。由于协方差矩阵CNEH是实对称矩阵, 所以存在正交矩阵H使其对角化。H由CNEH的特征向量构成, 将3个特征向量按列组装可得到：

$H=\left[ \begin{matrix}{{H}_{11}} & {{H}_{12}} & {{H}_{13}} \\{{H}_{21}} & {{H}_{22}} & {{H}_{23}} \\{{H}_{31}} & {{H}_{32}} & {{H}_{33}} \\\end{matrix} \right]$ （5）

根据线性代数理论, H与CNEH及特征值存在如下关系：

${{H}^{T}}{{C}_{NEH}}H\text{=}\left[ \begin{matrix}{{\lambda }_{1}} & {} & {} \\{} & {{\lambda }_{2}} & {} \\{} & {} & {{\lambda }_{3}} \\\end{matrix} \right]$ （6）

求得CNEH的特征值及特征向量后, 在误差椭球的主轴坐标系O° -UVW下, 便可得到标准形式的椭球方程：

$\frac{{{U}^{2}}}{{{\lambda }_{1}}}+\frac{{{V}^{2}}}{{{\lambda }_{2}}}+\frac{{{W}^{2}}}{{{\lambda }_{3}}}={{k}^{2}}$ （7）

误差椭球的尺寸可用3个主轴半径来表征, 即：

${{R}_{i}}\text{=}k\sqrt{{{\lambda }_{i}}}\quad $（i=1, 2, 3） （8）

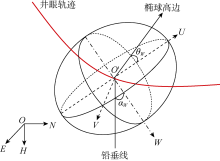
如图1所示, 根据井斜角、方位角和工具面角的定义, 选用误差椭球主轴W的井斜角α W、方位角

ϕ W及绕主轴W的偏转角θ W来表征误差椭球的姿态, 则有：

$\left\{ \begin{align}& \cos {{\alpha }_{W}}={{H}_{33}} \\& \tan {{\phi }_{W}}=\frac{{{H}_{23}}}{{{H}_{13}}} \\& \tan {{\theta }_{W}}=\frac{{{H}_{32}}}{-{{H}_{31}}} \\\end{align} \right.$ （9）

图1 误差椭球及姿态表征

在实际应用中, 往往需要确定特征值及特征向量与椭球主轴之间的对应关系。一般情况下, 可将靠近椭球高边方向的主轴作为U轴, 将靠近铅垂方向的主轴作为W轴, 并按右手法则确定V轴, 使U轴、V轴和W轴构成右手坐标系。

3 截面误差椭圆

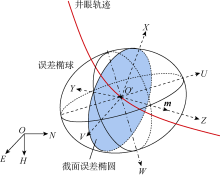
在钻井过程中, 往往需要分析井眼轨迹在水平面、铅垂面、法平面甚至任意平面上的误差, 用以评价井眼轨迹的不确定性。为此, 可用过误差椭球球心的平面来截取误差椭球, 在相应平面上得到截面误差椭圆（见图2）。

图2 误差椭球及截面误差椭圆

为建立截面误差椭圆的通用表征和计算方法, 用单位向量m表示任意姿态平面的法线方向, 则该法线的井斜角α m和方位角ϕ m确定了这个平面的空间姿态。如图2所示, 以误差椭球球心为原点, 建立截面坐标系O° -XYZ, 其中Z轴指向该平面的法线方向, X轴为该平面与过Z轴铅垂面的交线且指向高边方向, Y轴水平指向右侧。根据（3）式的协方差矩阵CNEH和坐标系间的旋转变换关系, 在截面坐标系O° -XYZ下协方差矩阵为：

${{C}_{XYZ}}=T{{C}_{NEH}}{{T}^{T}}$ （10）

其中 $T=\left[ \begin{matrix}\cos {{\alpha }_{m}}\cos {{\phi }_{m}} & \cos {{\alpha }_{m}}\sin {{\phi }_{m}} & -\sin {{\alpha }_{m}} \\-\sin {{\phi }_{m}} & \cos {{\phi }_{m}} & 0 \\\sin {{\alpha }_{m}}\cos {{\phi }_{m}} & \sin {{\alpha }_{m}}\sin {{\phi }_{m}} & \cos {{\alpha }_{m}} \\\end{matrix} \right]\, $

将CNEH分块并保留参数X和Y相关项, 可得到截面误差椭圆的方程为：

${{\left[ \begin{matrix}\delta X \\\delta Y \\\end{matrix} \right]}^{T}}{{\left[ \begin{matrix}\sigma _{X}^{2} & {{\sigma }_{XY}} \\{{\sigma }_{XY}} & \sigma _{Y}^{2} \\\end{matrix} \right]}^{-1}}\left[ \begin{matrix}\mathrm{ }\!\!\delta\!\!\text{ }X \\\mathrm{ }\!\!\delta\!\!\text{ }Y \\\end{matrix} \right]={{k}^{2}}$ （11）

截面误差椭圆的尺寸和姿态可用2个主轴半径和1个偏转角来表征, 计算公式为：

$\left\{ \begin{align}& {{r}_{i}}\text{=}k\sqrt{{{\lambda }_{i}}}\quad \left( i=12 \right) \\& \tan 2\theta =\frac{2{{\sigma }_{XY}}}{\sigma _{X}^{2}-\sigma _{Y}^{2}} \\\end{align} \right.$ （12）

其中 ${{\lambda }_{1}}^{2}=\sigma _{X}^{2}{{\cos }^{2}}\theta +{{\sigma }_{XY}}\sin 2\theta +\sigma _{Y}^{2}{{\sin }^{2}}\theta $

${{\lambda }_{2}}^{2}=\sigma _{X}^{2}{{\sin }^{2}}\theta -{{\sigma }_{XY}}\sin 2\theta +\sigma _{Y}^{2}{{\cos }^{2}}\theta $

常用的平面姿态包括水平面、铅垂面和法平面, 分别截取误差椭球得到水平截面、铅垂截面和法截面误差椭圆。以下3种情况为上述通用方法的特例, 只需适当选取法线的井斜角和方位角便可得到相应结果：①水平截面误差椭圆。取α m=ϕ m=0, 矩阵T为单位矩阵, 偏转角θ 从正北方向起算; ②铅垂截面误差椭圆。取α m=90° , ϕ m为铅垂平面的法向方位角, 此时偏转角θ 从铅垂方向起算; ③法截面误差椭圆。α m和ϕ m取值分别为井眼轨迹的井斜角α 和方位角ϕ , 此时偏转角θ 从井眼高边方向起算。

4 误差椭圆柱

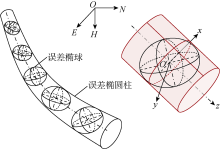
将井眼轨迹的误差椭球依次串联在井眼轨迹上, 误差椭球中心位于测点处。若用一个曲面来包络这些误差椭球, 将得到一个误差椭圆柱面, 由此构成的椭圆柱体可表征井眼轨迹的轴向包络误差及其沿井深的变化情况（见图3）。

图3 误差椭圆柱及构建原理

然而, 误差椭圆柱的形态十分复杂。首先, 井眼轨迹（即椭圆柱轴线）是三维挠曲线, 而非直线、圆弧等形状简单的曲线; 其次, 椭圆柱的横截面为椭圆形, 由于各测点处的误差椭球尺寸不同, 所以横截面椭圆的长短半径随井深变化; 再者, 由于各误差椭球的姿态不同, 所以椭圆柱面沿井眼轨迹是扭曲面。事实上, 误差椭圆柱面是不可展曲面, 并不是严格意义上的包络面。

为便于理解误差椭圆柱的形成原理, 假想地层为冰, 而误差椭球具有高温, 当误差椭球沿井眼轨迹移动时, 将消溶所触及到的冰体。这样, 在地层中所形成的“ 井筒” 就是误差椭圆柱, 而“ 井壁” 就是误差椭圆柱面。

如图3所示, 误差椭圆柱面与误差椭球相切, 其切点构成一条闭合曲线。在井眼坐标系O° -xyz下, 将这条闭合曲线投影到xy平面上, 得到一条闭合的投影曲线。这条投影曲线就是误差椭球在xy平面上投影区域的边界曲线, 也是误差椭圆柱在该测点处的横截面边界曲线。显然, 误差椭圆柱的横截面边界曲线为椭圆, 若能得到各测点处误差椭圆柱的横截面椭圆, 就可确定整个误差椭圆柱。

首先, 基于坐标系的旋转变换关系, 可得到井眼坐标系O° -xyz下的误差椭球方程。若用3个向量Bi （i=1, 2, 3）表示坐标系O° -UVW与坐标系O° -xyz间的转换矩阵B, 用向量r表示井眼轨迹位置误差坐标（x, y, z）, 则误差椭球方程为：

$\sum\limits_{i=1}^{3}{{{\left( \frac{{{\mathbf{B}}_{i}}\mathbf{r}}{{{R}_{i}}} \right)}^{2}}}=1$ （13）

其中 ${{\mathbf{B}}_{i}}=\left[ \begin{matrix}{{B}_{i1}}, & {{B}_{i2}}, & {{B}_{i3}} \\\end{matrix} \right]$

$\mathbf{r}=\left[ \begin{matrix}x, & y, & z \\\end{matrix} \right]$ $\mathbf{B}={{H}^{T}}{{A}^{T}}$

$A=\left[ \begin{matrix}\cos \alpha \cos \phi & \cos \alpha \sin \phi & -\sin \alpha \\-\sin \phi & \cos \phi & 0 \\\sin \alpha \cos \phi & \sin \alpha \sin \phi & \cos \alpha \\\end{matrix} \right]\, $

而椭圆柱面与误差椭球的相切条件为：

$\sum\limits_{i=1}^{3}{\frac{{{B}_{i3}}}{R_{i}^{2}}\left( {{\mathbf{B}}_{i}}\mathbf{r} \right)}=0$ （14）

消去向量r中的参数z, 便得到误差椭圆柱面与误差椭球的相切曲线在xy平面上的投影曲线方程：

${{\left[ \begin{matrix}x \\y \\\end{matrix} \right]}^{T}}\left[ \begin{matrix}{{F}_{11}} & {{F}_{12}} \\{{F}_{21}} & {{F}_{22}} \\\end{matrix} \right]\left[ \begin{matrix}x \\y \\\end{matrix} \right]=1$ （15）

其中 ${{F}_{11}}={{\sum\limits_{i=1}^{3}{\left( \frac{{{D}_{i1}}}{{{R}_{i}}} \right)}}^{2}}$ ${{F}_{12}}={{F}_{21}}=\sum\limits_{i=1}^{3}{\left( \frac{{{D}_{i1}}{{D}_{i2}}}{R_{i}^{2}} \right)}$

${{F}_{22}}={{\sum\limits_{i=1}^{3}{\left( \frac{{{D}_{i2}}}{{{R}_{i}}} \right)}}^{2}}$

${{D}_{ij}}={{B}_{ij}}-{{B}_{i3}}{{C}_{j}}\quad $（i=1, 2, 3; j=1, 2）

${{C}_{1}}=\frac{\sum\limits_{i=1}^{3}{\frac{{{B}_{i1}}{{B}_{i3}}}{R_{i}^{2}}}}{\sum\limits_{i=1}^{3}{{{\left( \frac{{{B}_{i3}}}{{{R}_{i}}} \right)}^{2}}}}$ ${{C}_{2}}=\frac{\sum\limits_{i=1}^{3}{\frac{{{B}_{i2}}{{B}_{i3}}}{R_{i}^{2}}}}{\sum\limits_{i=1}^{3}{{{\left( \frac{{{B}_{i3}}}{{{R}_{i}}} \right)}^{2}}}}$

若用矩阵G表示矩阵F的逆矩阵, 则误差椭圆柱的横截面椭圆主轴半径及偏转角为：

$\left\{ \begin{align}& r_{1}^{2}={{G}_{11}}{{\cos }^{2}}\theta +{{G}_{12}}\sin 2\theta +{{G}_{22}}{{\sin }^{2}}\theta \\& r_{2}^{2}={{G}_{11}}{{\sin }^{2}}\theta -{{G}_{12}}\sin 2\theta +{{G}_{22}}{{\cos }^{2}}\theta \\& \tan 2\theta =\frac{2{{G}_{12}}}{{{G}_{11}}-{{G}_{22}}} \\\end{align} \right.$ （16）

将各测点处的横截面椭圆沿井眼轨迹串联起来就构成了误差椭圆柱, 可用于评价井眼轨迹的轴向包络误差及其沿井深变化情况。

5 实例分析

某水平井按行业规程实施测量和井眼轨迹计算, 得到以真北为参考基准的计算结果（见表1）。该井的地磁场强度为56 356.51 nT, 磁偏角为-10.60° , 磁倾角为64.72° , 子午线收敛角为0.876° , 误差椭球放大系数取2.0。采用无轴向校正及BHA下坠等基本MWD（随钻测量）误差模型, 按本文的井眼轨迹误差表征和计算方法, 得到如表2和表3所示的评价结果（限于篇幅, 表1— 表3仅列出部分数据）。

表1 井眼轨迹计算结果
表2 井眼轨迹误差椭球及误差椭圆柱评价结果
表3 井眼轨迹截面误差椭圆评价结果
6 结论

井越深井眼轨迹误差越大, 深井超深井的井眼轨迹位置误差可达数十米。要提高井眼轨迹监测与控制精度, 首先必须严格按行业规程进行测斜作业, 包括定期校验测量仪器、现场检验地磁场及重力场、按行业规范确定MWD无磁间距和测点间距等。

井眼轨迹的误差椭球主轴与井眼坐标系的坐标轴不重合。用误差椭球主轴的井斜角、方位角及偏转角来表征误差椭球的空间姿态, 具有明确的物理意义, 便于工程应用。

井眼轨迹截面误差椭圆的概念及算法具有通用性, 可评价井眼轨迹在水平面、铅垂面、法平面、甚至任意平面上的误差, 还可用于中靶概率分析等。

井眼轨迹的误差椭圆柱可评价井眼轨迹的轴向包络误差及其沿井深变化情况, 误差椭圆柱横截面椭圆的最大主轴半径大于等于法截面误差椭圆的最大主轴半径, 甚至有可能大于误差椭球的最大主轴半径。

符号注释：

A、B、H、F、T— — 坐标变换矩阵; C— — 协方差矩阵; E— — 东坐标, m; e— — 井眼轨迹关于N、E、H坐标的误差向量; Glob— — 全局误差; G— — 矩阵F的逆矩阵; H— — 垂深, m; h— — 误差源的编号; k— — 误差椭球的放大系数, 无因次; L— — 井深, m; m— — 法向量; N— — 北坐标, m; Rand— — 随机误差; R— — 误差椭球的主轴半径, m; r— — 误差椭圆的主轴半径, m; r— — 井眼轨迹的位置误差向量; Syst— — 系统误差; U, V, W— — 误差椭球主轴坐标系, m; Well— — 单井误差; X— — 截面坐标系的高边坐标, m; x— — 井眼高边坐标, m; Y— — 截面坐标系的右向坐标, m; y— — 井眼右向坐标, m; Z— — 截面坐标系的法向坐标, m; z— — 井眼切向坐标, m; α — — 井斜角, （° ）; ε — — 误差源; ϕ — — 方位角, （° ）; λ — — 协方差矩阵的特征值, m2; θ — — 误差椭球及椭圆的偏转角, （° ）; σ — — 误差大小, 或方差及协方差, m2; $\frac{\partial \mathbf{p}}{\partial \varepsilon }$— — 权函数向量; $\frac{\text{d}\mathbf{r}}{\text{d}\mathbf{p}}$— — 测量误差对N、E、H坐标的影响矩阵。

The authors have declared that no competing interests exist.

参考文献
[1] 郭艳利, 孙宝江, 高永海, 等. 碳酸盐岩储集层钻井井涌特征及井涌风险评价[J]. 石油勘探与开发, 2017, 44(3): 431-438.
GUO Yanli, SUN Baojiang, GAO Yonghai, et al. Gas kick during carbonate reservoirs drilling and its risk assessment[J]. Petroleum Exploration and Development, 2017, 44(3): 431-438. [本文引用:1]
[2] BROOKS A G, WILSON H. An improved method for computing wellbore position uncertainty and its application to collision and target intersection probability analysis[R]. SPE 36863, 1996. [本文引用:5]
[3] WILLIAMSON H S. Accuracy prediction for directional MWD[R]. SPE 56702, 1999. [本文引用:5]
[4] WILLIAMSON H S. Accuracy prediction for directional measurement while drilling[J]. SPE Drilling & Completion, 2000, 15(4): 221-233. [本文引用:5]
[5] BROOKS A G, WILSON H, JAMIESON A L, et al. Quantification of depth accuracy[R]. SPE 95611, 2005. [本文引用:5]
[6] GRINDROD S J, CLARK P J, LIGHTFOOT J D, et al. OWSG stand ard survey tool error model set for improved quality and implementation in directional survey management[R]. SPE 178843, 2016. [本文引用:3]
[7] TORKILDSEN T, HAVARSTEIN S T, WESTON J L, et al. Prediction of wellbore position accuracy when surveyed with gyroscopic tools[R]. SPE 90408, 2008. [本文引用:3]
[8] EKSETH R, TORKILDSEN T, BROOKS A G, et al. The reliability problem related to directional survey data[R]. SPE 103734, 2006. [本文引用:3]
[9] EKSETH R, TORKILDSEN T, BROOKS A G, et al. High integrity wellbore surveys: Methods for eliminating gross errors[R]. SPE 105558, 2007. [本文引用:3]
[10] JAMIESON A. Introduction to wellbore positioning[M]. Scotland : University of the Highland s & Island s, 2017. [本文引用:5]
[11] WOLFF C J M, de WARDT J P. Borehole position uncertainty-analysis of measuring methods and derivation of systematic error model[J]. Journal of Petroleum Technology, 1981, 33(12): 2338-2350. [本文引用:1]
[12] 刘修善. 导向钻具定向造斜方程及井眼轨迹控制机制[J]. 石油勘探与开发, 2017, 44(5): 788-793.
LIU Xiushan. Directional deflection equations for steerable drilling tools and the control mechanism of wellbore trajectory[J]. Petroleum Exploration and Development, 2017, 44(5): 788-793. [本文引用:1]
[13] 董本京, 高德利, 柳贡慧. 井眼轨迹不确定性分析方法的探讨[J]. 天然气工业, 1999, 19(4): 59-63.
DONG Benjing, GAO Deli, LIU Gonghui. Discussion on the analytical method of well track uncertainty[J]. Natural Gas Industry, 1999, 19(4): 59-63. [本文引用:1]
[14] 柳贡慧, 董本京, 高德利. 误差椭球(圆)及井眼交碰概率分析[J]. 钻采工艺, 2000, 23(3): 5-12.
LIU Gonghui, DONG Benjing, GAO Deli. Probability analysis of error ellipsoid (ellipse) and hole intersection[J]. Drilling & Production Technology, 2000, 23(3): 5-12. [本文引用:1]