引用本文
夏文鹤, 孟英峰, 唐波, 官文婷. 变内径钻柱中微波传输衰减规律[J]. 石油勘探与开发, 2018,45(3): 500-506.
XIA Wenhe, MENG Yingfeng, TANG Bo, GUAN Wenting. Attenuation of microwave transmission in a diameter-variable drill string bore[J]. Petroleum Exploration & Development, 2018,45(3): 500-506.  
Doi: 10.11698/PED.2018.03.15
Permissions
Copyright©2018, 《石油勘探与开发》编辑部
《石油勘探与开发》编辑部 所有
变内径钻柱中微波传输衰减规律
夏文鹤1,2, 孟英峰1, 唐波3, 官文婷4
1. “油气藏地质及开发工程”国家重点实验室 西南石油大学,成都 610500;
2. 西南石油大学电气信息学院,成都 610500
3. 中国石化胜利石油工程有限公司钻井工艺研究院,山东东营 257017
4. 中国石油西南油气田公司工程技术研究院,成都 610050

第一作者简介：夏文鹤（1978-）,男,四川成都人,博士,西南石油大学电气信息学院副教授,主要从事气体钻井井下随钻测量方面的研究工作。地址：四川省成都市新都区新都大道8号,西南石油大学电气信息学院,邮政编码：610500。E-mail：swpuxwh@swpu.edu.cn

收稿日期: 2017-12-10
基金项目: “十三五”国家科技重大专项（2016ZX05021-003-003HZ）
摘要

为确定钻柱内孔微波传输的最佳工作频点,获取微波信道的衰减规律及有效传输距离,将钻柱内孔视为超长不规则有耗圆波导,采用电磁波耦合理论计算了微波传输最佳工作频点,分析了波导中的微波模式,采用微波传输等效电路法建立了信道模型及信号衰减规律模型。针对超长钻柱,提出单位长度功率衰减系数从而对有效传输距离进行简化分析。研究表明,139.7 mm（5.5 in）和127.0 mm（5 in）API标准钻杆最佳工作频点分别为2.04 GHz和2.61 GHz,钻柱内孔沿轴向存在多个内径渐变段和突变点,微波传输存在大量反射过程,信道的阻抗变化是影响传输性能的主要因素。室内及现场测试结果表明,建立的微波传输衰减规律模型计算结果准确,可用于微波传输随钻监测系统的设计。图5表4参18

关键词: 气体钻井; 随钻测量; 微波传输; 钻柱内孔; 最佳频点; 圆波导; 有效传输距离
中图分类号:TE927 文献标志码:A 文章编号:1000-0747(2018)03-0500-07
Attenuation of microwave transmission in a diameter-variable drill string bore
XIA Wenhe1,2, MENG Yingfeng1, TANG Bo3, GUAN Wenting4
1. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu 610500, China
2. School of Electrical and Information Engineering, Southwest Petroleum University, Chengdu 610500, China
3. Drilling Technology Research Institute of Shengli Petroleum Engineering Corporation Limited, Sinopec, Dongying 257017, China
4. Engineering Technology Research Institute, PetroChina Southwest Oil & Gasfield Company, Chengdu 610050, China;
Abstract

With the drill string hole being regarded as an ultra-long irregular lossy cylindrical waveguide, the optimal frequency point for microwave transmission was calculated according to the electromagnetic wave coupling theory, the attenuation law and efficient transmission distance of microwave channel were obtained and the microwave mode in the waveguide was analyzed. Furthermore, the channel model and signal attenuation model were established by the microwave transmission equivalent circuit method. The power attenuation coefficient per unit of length was proposed to simplify the analysis on effective transmission distance for the ultra-long drill string. The optimal frequency points of 139.7 mm (5.5 in) and 127 mm (5 in) API drill pipes are 2.04 GHz and 2.61 GHz, respectively, and there are several inner diameter varying sections and break points in the drill string hole along the axial direction. The microwave transmission suffers a lot of reflections. The channel impedance change is a key factor affecting the transmission quality. The lab and field tests reveal that the attenuation model established in this paper is accurate, and it is helpful for guiding the design of microwave transmission measurement while drilling system.

Keyword: gas drilling; measure while drilling; microwave transmission; drill string bore; optimal frequency point; cylindrical waveguide; effective transmission distance
0 引言

气体钻井对随钻安全监测系统有非常高的要求, 但在这一关键技术领域仍然存在一些难题[1]。近年来, 电磁波随钻测量（EM-MWD）技术因其传输速率高且不依赖钻井液脉冲等优点成为随钻监测领域的研究热点[2]。该技术将整个钻柱作为天线, 通过地层传播电磁波信号以传输井下信息[3], 因此可应用于采用气体作为循环介质的气体钻井。但是电磁波信号在传输过程中会随地层加深而迅速衰减, 且难以在低电阻率地层和非均匀地层传输[4], 井深超过有效传输距离后难以从地面接收信号并提取有效信息[5]。此外, 施工现场的电磁环境也会对电磁波信号产生极大干扰, 使得目前EM-MWD技术的信号有效传输距离仍较短[5]。虽然可采用有线加无线接力、配置无线中继器等方法提升EM-MWD技术信号传输深度, 但有线加无线接力的方式操作复杂, 接头处信号传输不稳定, 可靠性较差; 而使用无线中继器难以保证多套信号收发装置在井筒高温高压条件下的稳定性和持久性[6]。因此总体而言, EM-MWD技术目前尚不成熟。这导致在气体钻井领域至今还未形成一套较为实用的随钻监测系统, 大部分气体钻井作业过程中只能依靠地面监测系统对井下状况进行推测, 大幅降低了监测的准确性和时效性[7]。

基于EM-MWD的技术思路, 可以在近钻头位置安装随钻测量短节采集信号, 利用钻柱内孔作为微波波导, 将井下测量信息传输到地面, 并进行数据分析和处理, 这就是微波传输随钻测量（MT-MWD）技术。该技术在钻柱内孔中激发、传播微波信号, 能够有效避免地层因素对微波信道的影响, 从而提高传输效率, 并形成多级中继链式传输网络, 增加测传深度, 以实现大量井下测试数据高速实时地传输到地面, 满足气体钻井随钻测量的需求[8]。由于该技术不受地层电阻率的影响, 因此本文研究的重点为信道最佳工作频点的设置、微波在钻柱内孔中传输时的衰减规律以及有效传输距离的确定。

1 钻柱内孔微波传输波形及最佳频点
1.1 传输可行性及耦合波形

微波是波长为厘米级或毫米级的电磁波, 用普通的电缆或导线传输会产生很大损耗, 因此微波的馈送一般采用截面为矩形或圆形的金属管道, 称为波导。钻柱由多段不同的金属管连接而成, 在内孔激发对应频段的微波信号, 即可构成微波信道。根据瑞利准则[9], 钻柱内孔可视为理想导体。若在钻柱接头段内孔激发微波信号, 则整个钻柱内孔可视为1段同轴的不连续圆波导, 并向两边延伸[10]。由波导理论可知, 圆波导内只能存在TM波（横磁波）或TE波（横电波）。根据波导内电磁波传播最基本的波动方程[11]可得到截止波长表达式：

$\frac{\lambda _{ij, \text{TM}}^{{}}}{a}=\frac{\text{ }\!\!\pi\!\!\text{ }}{{{\rho }_{ij}}}$ （1）

$\frac{{{\lambda }_{ij, \text{TE}}}}{a}=\frac{\text{ }\!\!\pi\!\!\text{ }}{{{{{\rho }'}}_{ij}}}$ （2）

ρ ij和${{{\rho }'}_{ij}}$为常数, 可以查表获得。表1、表2分别给出了若干个TM波和TE波的λ ij/a值。

表1 圆波导中TMij波的λ ij/a值
表2 圆波导中TEij波的λ ij/a值

根据波导内径及表1、表2中的数据确定各模式波形的截止波长, 再根据工作频点确定微波信号的实际波长。若实际波长小于截止波长, 则波导中该模式波形未截止, 即存在该模式波形。波导内微波传输的衰减主要缘于波导内壁的表面电流和波导内部的填充介质。若忽略钻柱内气体填充介质的影响, 则各TM、TE波形在波导中的衰减系数分别为：

$\alpha _{ij, \text{TM}}^{{}}=\frac{2{{R}_{\text{s}}}}{a{{Z}_{0}}\sqrt{1-{{\left( \frac{\lambda }{\lambda _{ij, \text{TM}}^{{}}} \right)}^{2}}}}$ （3）

其中 ${{Z}_{0}}=\sqrt{{{{\mu }_{0}}}/{{{\varepsilon }_{0}}}\; }$ ${{R}_{\text{s}}}=\sqrt{{\text{ }\!\!\pi\!\!\text{ }f\mu }/{\sigma }\; }$

${{\alpha }_{ij, \text{TE}}}=\frac{2{{R}_{\text{s}}}}{a{{Z}_{0}}\sqrt{1-{{\left( \frac{\lambda }{{{\lambda }_{ij, \text{TE}}}} \right)}^{2}}}}\left[ {{\left( \frac{\lambda }{{{\lambda }_{ij, \text{TE}}}} \right)}^{2}}+\frac{{{n}^{2}}}{{{{{\rho }'}}_{ij}}^{2}-{{n}^{2}}} \right]$ （4）

显然, 衰减系数与波形有关, 各种波形截止波长差别较大, 导致各种波形的衰减系数差别较大。其中圆波导最低次基模TE11波形的衰减系数最小, 而次高模TM01及第2次高模TE21波形的衰减系数远大于TE11波形。若在钻柱内孔中激发出TM01和TE21波形, 会迅速衰减。但微波激发时其能量会按比例耦合于不同波形, 假设采用3种波形共存的多模方式传输, 则其中TE11波形的能量仅为单模方式的1/3, 另外2/3的能量会激发为迅速消耗衰减的TM01和TE21波形[12]。因此, 与单模传输方式相比多模传输方式总能量衰减速度大幅提高, 故传输过程应采用单模传输方式, 并抑制衰减系数大的波形的形成, 以增加微波的有效传输距离。钻柱内孔结构固定且空间狭小, 难以安装复杂的电磁机构, 因此主要采用设置最佳工作频点的方式实现单模传输。

1.2 最佳工作频点

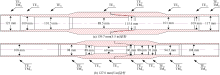
钻柱内孔主要是钻杆内孔, 因此设置微波工作频点时应保证微波能在钻杆最小内径段传播, 并保证一定的信号带宽。以气体钻井常用的139.7 mm（5.5 in）和127.0 mm（5 in）API标准钻杆（见图1）为例, 其最小内径分别为88.5 mm和69.0 mm。

图1 钻柱接头结构尺寸图

由表2可知, 若要在139.7 mm和127.0 mm钻杆中激发最低次基模TE11波传输, 截止波长分别为151.00 mm和117.73 mm, 即工作频点应分别高于1.98 GHz和2.55 GHz。根据国际电信联盟的频带划分, 在2.0~2.6 GHz频段, 可以采用的物联网通信协议主要为Zigbee通信协议和蓝牙通信协议。这两种协议均需要在该频段设置16个间隔为5 MHz的信道, 即在工作频点处保留± 40 MHz共80 MHz带宽[13]。频点越高微波振荡激发元件功耗越大, 且微波在钻柱内孔粗糙表面的导体损耗越大, 因此应尽量降低工作频点。此外, 为了保证TE11波形的有效激发, TE11波形工作频点应与波形最低激发频点存在20 MHz频带间隔, 故139.7 mm和127.0 mm API标准钻杆最佳频点分别设置为2.04 GHz和2.61 GHz。

虽然该最佳频点会在内径较大的管段激发出TM01波形（见图1）, 但是根据微波模式转换条件[14]可知：若将源激发点设置于仅能激发出TE11波形的管段, 则在钻柱弯曲幅度较小的条件下, 不具备波形转换条件, 即使钻柱内孔中存在多个内径渐变的过渡管段和突变点, 整个钻柱内孔仍可保持单模方式进行传输。同时单模传输时波形能量更集中, 也减少了各模式之间的干扰损耗, 传输特性更好。此外也有利于简化传输分析模型, 减少分析误差[15]。

2 钻柱内孔变径结构对微波传输的影响

（3）式、（4）式求得的衰减系数仅考虑波导内壁导体损耗因素, 适用于等径波导元件。但钻柱内孔为超长不规则圆波导, 由图1可知钻柱内孔波导存在多个变径段和内径突变点, 会产生微波信号的反射, 增加信号衰减。因此除导体损耗外, 应充分考虑由波导结构引起的损耗。在单模传输条件下, 该损耗可采用等效电路法确定。

2.1 钻柱内孔波导模型

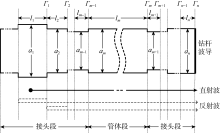
根据钻柱结构图纸与实测尺寸, 用紧密连接后钻柱内壁呈现的结构建立钻柱内孔波导模型, 忽略螺纹及小缝隙因素。通过连接后钻柱结构剖视图（见图2）可知, 钻柱内孔内径突变点一般存在于钻具公接头顶面, 其余部分内径变化均为渐变方式。将内径固定管段视为等径波导段; 将内径不连续的突变点视为波导接头; 将轴向长度不超过1/4波长的短内径渐变段视为短渐变波导段; 将轴向长度超过1/4波长的长内径渐变段视为长渐变波导段[16]。

图2 钻柱结构剖视图

2.2 钻柱内孔波导等效电路模型

根据钻柱内孔单模传输状况, 采用微波传输线理论等效电路法[11], 可进一步将钻柱内孔信道分为3种情况进行分析：等径波导直接等效为1段有耗传输线; 内径变化较小的短渐变波导或内径突变的连接点, 等效为1个传输线接头, 接头两端分别与原等径波导连接; 内径变化较大的长渐变波导, 等效为多个阶梯波导的级联。则等效后的钻柱内孔波导段可视为由n段长度为ln、内径为an的等径波导段与n个反射面的级联, 如图3所示。

图3 钻柱内孔波导示意图

图3中有耗传输线的阻抗用其填充空气介质时的等效阻抗计算：

${{Z}_{n}}=\frac{520}{\sqrt{1-{{\left( \frac{\lambda }{\lambda _{n}^{{}}} \right)}^{2}}}}$ （5）

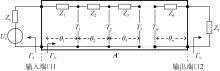
两有耗传输线（阻抗为Zn-1、Zn）之间采用波导接头Tm连接, 则波导等效电路[11]如图4所示。

图4 钻柱内孔波导等效电路

由微波传输线理论, 对于阻抗为Zn的有耗传输线, 其转移参量矩阵为：

${{A}_{n}}=\left( \begin{matrix} \text{cos}{{\theta }_{n}} & {{Z}_{n}}+\text{i}\, \text{sin}{{\theta }_{n}} \\ \text{i}\, \text{sin}{{\theta }_{n}} & \text{i}\, {{Z}_{n}}\text{sin}{{\theta }_{n}}+\text{cos}{{\theta }_{n}} \\\end{matrix} \right)$ （6）

其中 ${{\theta }_{n}}={{\beta }_{n}}{{l}_{n}}$

对于波导接头Tm, 转移参量矩阵为：

${{A}_{m}}=\left( \begin{matrix} \sqrt{\frac{{{Z}_{m+1}}}{{{Z}_{m}}}} & 0 \\ 0 & \sqrt{\frac{{{Z}_{m}}}{{{Z}_{m+1}}}} \\\end{matrix} \right)$ （7）

根据微波网络级联原则, 对于级联等效波导段, 其2× 2维波导转移矩阵为：

${A}'=\left( \begin{matrix} A & B \\ C & D \\\end{matrix} \right)=$

$\left( \begin{matrix} \text{cos}{{\theta }_{1}} & {{Z}_{1}}+\text{i}\, \text{sin}{{\theta }_{1}} \\ \text{i}\, \text{sin}{{\theta }_{1}} & \text{i}\, {{Z}_{1}}\text{sin}{{\theta }_{1}}+\text{cos}{{\theta }_{1}} \\\end{matrix} \right)\left( \begin{matrix} \sqrt{\frac{{{Z}_{2}}}{{{Z}_{1}}}} & 0 \\ 0 & \sqrt{\frac{{{Z}_{1}}}{{{Z}_{2}}}} \\\end{matrix} \right)\times $

$\left( \begin{matrix} \text{cos}{{\theta }_{2}} & {{Z}_{2}}+\text{i}\, \text{sin}{{\theta }_{2}} \\ \text{i}\, \text{sin}{{\theta }_{2}} & \text{i}\, {{Z}_{2}}\text{sin}{{\theta }_{2}}+\text{cos}{{\theta }_{2}} \\\end{matrix} \right)\left( \begin{matrix} \sqrt{\frac{{{Z}_{3}}}{{{Z}_{2}}}} & 0 \\ 0 & \sqrt{\frac{{{Z}_{2}}}{{{Z}_{3}}}} \\\end{matrix} \right)\times \cdots \times $

$\left( \begin{matrix} \text{cos}{{\theta }_{n-1}} & {{Z}_{n-1}}+\text{i}\, \text{sin}{{\theta }_{n-1}} \\ \text{i}\, \text{sin}{{\theta }_{n-1}} & \text{i}\, {{Z}_{n-1}}\text{sin}{{\theta }_{n-1}}+\text{cos}{{\theta }_{n-1}} \\\end{matrix} \right)\left( \begin{matrix} \sqrt{\frac{{{Z}_{n}}}{{{Z}_{n-1}}}} & 0 \\ 0 & \sqrt{\frac{{{Z}_{n-1}}}{{{Z}_{n}}}} \\\end{matrix} \right)\times $

$\left( \begin{matrix} \text{cos}{{\theta }_{n}} & {{Z}_{n}}+\text{i}\, \text{sin}{{\theta }_{n}} \\ \text{i}\, \text{sin}{{\theta }_{n}} & \text{i}\, {{Z}_{n}}\text{sin}{{\theta }_{n}}+\text{cos}{{\theta }_{n}} \\\end{matrix} \right)$ （8）

为充分利用钻柱结构的周期性, 减少计算量, （8）式可由1根钻杆作为基本单元建立转移矩阵。则由N根钻杆连接后构成的转移矩阵为：

${{{A}'}_{N}}=\prod\limits_{N}{{{A}'}}=\left( \begin{matrix} {{A}_{N}} & {{B}_{N}} \\ {{C}_{N}} & {{D}_{N}} \\\end{matrix} \right)$ （9）

进一步采用微波元件的分析方法, 将微波输入的平面视为输入端口1, 微波输出的平面视为输出端口2, 则N根钻杆连接后的级联钻杆波导散射矩阵为：

${{S}_{N}}=\left( \begin{matrix} {{S}_{N, 11}} & {{S}_{N, 12}} \\ {{S}_{N, 21}} & {{S}_{N, 22}} \\\end{matrix} \right)=$

$\left( \begin{matrix} \frac{{{A}_{N}}+{{B}_{N}}-{{C}_{N}}-{{D}_{N}}}{{{A}_{N}}+{{B}_{N}}+{{C}_{N}}+{{D}_{N}}} & \frac{2\left| {{{{A}'}}_{N}} \right|}{{{A}_{N}}+{{B}_{N}}+{{C}_{N}}+{{D}_{N}}} \\ \frac{2}{{{A}_{N}}+{{B}_{N}}+{{C}_{N}}+{{D}_{N}}} & \frac{-{{A}_{N}}+{{B}_{N}}-{{C}_{N}}+{{D}_{N}}}{{{A}_{N}}+{{B}_{N}}+{{C}_{N}}+{{D}_{N}}} \\\end{matrix} \right)$ （10）

将信号发射器视为信号源, 电压为Us, 内阻抗为Zs, 对应连接波导的特性阻抗为Z1; 将信号接收器视为负载, 内阻抗为ZL, 对应连接波导的特性阻抗为Zn。则输入端口向信号源的反射系数、输出端口向负载的反射系数、N根钻杆级联波导输入反射系数分别为：

${{\Gamma }_{\text{s}}}=\frac{{{Z}_{\text{s}}}-{{Z}_{1}}}{{{Z}_{\text{s}}}+{{Z}_{1}}}$ （11）

${{\Gamma }_{\text{L}}}=\frac{{{Z}_{\text{L}}}-{{Z}_{n}}}{{{Z}_{\text{L}}}+{{Z}_{n}}}$ （12）

${{\Gamma }_{N}}={{S}_{N, 11}}+\frac{{{S}_{N, 12}}{{S}_{N, 21}}{{\Gamma }_{\text{L}}}}{1-{{S}_{N, 22}}{{\Gamma }_{\text{L}}}}$ （13）

若信号发射器发射功率为Pt, N根钻杆连接后接收器能接收到的实际功率为PN, 则对于钻柱内孔微波信道, 由不同波导段阻抗变化所形成的阻抗传输系数和损耗功率分别为[11]：

${{G}_{\text{z}}}=\frac{{{P}_{N}}}{{{P}_{\text{t}}}}=\frac{{{\left| {{S}_{N, 22}} \right|}^{2}}\left( 1-{{\left| {{\Gamma }_{\text{s}}} \right|}^{2}} \right)\left( 1-{{\left| {{\Gamma }_{\text{L}}} \right|}^{2}} \right)}{{{\left| 1-{{\Gamma }_{\text{s}}}{{\Gamma }_{N}} \right|}^{2}}{{\left| 1-{{S}_{N, 22}}{{\Gamma }_{\text{L}}} \right|}^{2}}}$ （14）

${{P}_{\text{sz}}}=\left( 1-{{G}_{\text{z}}} \right){{P}_{\text{t}}}$ （15）

2.3 单位长度功率衰减系数计算模型

由于钻柱长度一般大于1 000 m, 且随着钻进过程会逐渐延长, 因此应视为超长不规则圆波导。若对整根钻柱的衰减规律进行精确分析, 则会因为计算量太大而难以实现。但钻柱结构具有一定周期性, 因此可将一、两根钻杆作为传输单元, 建立一、两根钻杆的传输模型, 并计算其单位长度的平均衰减系数, 进而推导整个钻柱的衰减规律。由上述信道模型的分析可知, 钻柱内孔结构对微波传输的影响主要体现为由变径结构造成的阻抗变化。若传输单元的长度为L, 则钻柱内孔单位长度功率衰减系数为[17]：

$\alpha =\frac{\text{ln}\frac{{{P}_{\text{sz}}}}{{{P}_{\text{t}}}}}{L}$ （16）

3 模型验证及现场应用

测试装置位于“ 油气藏地质及开发工程” 国家重点实验室, 测试模型由4根完整的139.7 mm（5.5 in）API钻杆和1个钻杆母接头短节连接而成。首先采用1根钻杆进行测试, 将发射天线安装在钻杆管体段的始端, 将接收天线安装在母接头短节中管体段的始端, 即收发天线之间存在8.10 m管体段和1对1.15 m上扣的连接接头, 距离约为9.25 m, 与1根连接后完整的钻杆单元长度相同[18]（见图2）。测试装置的接收天线可沿轴向在8.45~9.25 m距离内按20 cm步进移动, 模型内壁无明显锈蚀。

3.1 单位长度功率衰减系数计算模型验证

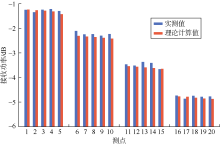
根据139.7 mm（5.5 in）API钻杆内孔结构, 利用本文模型计算得到单位长度功率衰减系数为0.133 dB/m。改变接收天线的位置, 用频谱分析仪测试2.4 GHz频点的接收功率。将接收天线在不同位置的实际接收功率与采用单位长度功率衰减系数计算的接收功率进行比较, 验证一致性。每根钻杆设置5个测试点, 1号钻杆测试完成后, 将1号、2号钻杆连接, 再将母头短节连接到2号钻杆的公头端, 3号、4号钻杆以此类推。各测试点处收发天线之间的距离如表3所示。测试结果如图5所示。

表3 功率衰减测试实验各测点处收发天线距离

图5 功率衰减状况对比图

由于钻柱长度增加量以单根钻杆长度为单位, 因此图5中理论计算与实测的接收功率总体呈阶梯状减小的趋势。而对于每根钻杆的5个测试点, 理论计算值基本按线性规律下降。由于电磁波传输阻抗存在1/4波长的变换性及1/2波长的重复性, 而测试过程中各测试点的距离并未按1/2波长增加, 因此各测试点阻抗值存在波动, 导致实测值也存在波动。但实测值与理论计算值的最大差值仅为0.22 dB, 验证了理论计算的正确性, 也充分说明由结构体自身阻抗变化所形成的功率损耗是影响微波传输的主要因素。

3.2 现场应用

利用钻柱内孔微波传输样机在四川盆地元陆29井进行了3趟钻的现场试验。元陆29井是1口预探直井, 该井设计井深4 930 m。二开采用气体钻井方式从702 m钻至3 402 m, 采用Φ 311.2 mm钻头, 钻压200~260 kN, 转速60~90 r/min, 注气排量控制在180~220 m3/min, 试验在二开气体钻井过程中进行。

钻具组合中采用127.0 mm（5 in）API标准钻杆进行钻井作业, 但钻杆主要包括两个批次钻杆, 新旧程度不同, 试验采用2.65 GHz频点进行钻柱内孔微波通信。根据钻杆内孔结构及试验前在管具中心对上井钻杆进行现场测试的数据, 通过软件建立了微波传输衰减规律模型。分析结果表明, 对于较新钻杆, 其衰减系数约为0.253 dB/m; 对于较旧钻杆, 其衰减系数约为0.295 dB/m。若将天线最低接收功率设为-50 dB, 则较新钻杆传输距离应高于194 m（21根钻杆）, 较旧钻杆传输距离应高于166 m（18根钻杆）。

由表4可知, 整个试验过程中, 系统样机实现最大测深3 077 m, 两级中继间最长传输距离为204.34 m。除去个别异常钻杆, 对于较旧钻杆, 微波传输距离能稳定在174 m（19根钻杆）左右; 对于较新钻杆, 微波传输距离能稳定在200 m左右（22根钻杆）。这与计算结果基本吻合, 验证了钻柱内孔微波传输的可行性及微波传输衰减规律模型的正确性。试验过程实时获取了井斜、方位等数据, 测得井底最高温度为56 ℃。全部设备工作正常, 未影响正常的钻进作业施工。设备最长工作时间120 h, 起钻取出后仍可继续正常工作, 说明传输系统具备继续增加中继器以提高测传深度的潜力。试验过程中, 井下最大测传速率为1.194 kb/s, 地面接收到的数据格式正确, 无乱码现象, 说明系统具备进一步增大测传速率的潜力。

表4 元陆29井第3趟钻微波中继加入情况
4 结论

钻柱为长直管状, 沿轴向存在内径渐变段和突变点, 其内孔可视为超长同轴不连续有耗圆波导, 建立2~3 GHz频段微波信道。139.7 mm（5.5 in）和127.0 mm（5 in）API标准钻杆最佳工作频点分别为2.04 GHz和2.61 GHz, 最佳工作频点可保证整个信道采用单模工作方式以避免多模损耗并减少导体损耗。

钻柱内孔变径结构会导致信道阻抗沿轴向发生多次变化, 增大微波损耗, 这是影响传输性能的主要因素。本文建立的微波传输衰减规律模型展示了微波在钻柱内孔信道中损耗的状况, 该模型的计算结果准确, 为确定信道传输距离等重要参数提供了依据, 对微波传输随钻监测系统的设计具有指导意义。根据理论计算和实际测试, 采用普通全向天线在钻柱中激发微波信号, 其单位长度功率衰减系数小于0.3 dB/m。若进一步采用圆极化定向天线将微波激发能量集中在轴向, 或提高接收元件灵敏度, 并使用内孔变径结构较少的钻具, 会大幅降低衰减系数, 从而提高有效传输距离。在有效距离范围内安装信号中继器形成链式传输网, 还可大幅延伸实际传输距离。

本文中分析和测试的对象主要是139.7 mm（5.5 in）和127.0 mm（5 in）API钻杆, 但微波信道模型建立和测试的方法可应用于其他类型的钻杆、套管、钻柱接头以及类似非标准波导元件的分析。由于钻柱结构的周期性, 采用了单根钻杆单元平均衰减系数模型对信道传输性能进行评价, 可大幅简化超长钻柱内孔信道的传输性能分析。

符号注释：

a— — 波导内径, m; an— — 等径波导段内径, m; A, B, C, D, AN, BN, CN, DN— — 中间变量; Am— — 波导接头的转移参量矩阵; An— — 有耗传输线的转移参量矩阵; ${{{A}'}_{N}}$— — N根钻杆连接后构成的波导转移矩阵; A° — — 波导转移矩阵; f— — 工作频点, Hz; Gz— — 阻抗传输系数; ln— — 等径波导段长度, m; L— — 传输单元长度, m; m— — 等径波导段编号; n— — 等径波导段数目; PN— — N根钻杆连接后接收器能接收到的实际功率, W; Psz— — 损耗功率, W; Pt— — 信号发射器发射功率, W; SN— — N根钻杆连接后的级联钻杆波导散射矩阵; SN, 11— — 级联钻杆波导输入端口1的电压反射系数; SN, 12— — 级联钻杆波导输出端口2到输入端口1的电压传输系数; SN, 21— — 端口1到端口2的电压传输系数; SN, 22— — 端口2的电压反射系数; Tm— — 波导接头; Us— — 信号源电压, V; ZL— — 负载内阻抗, Ω ; Zn— — 有耗传输线的阻抗, Ω ; Zs— — 信号源内阻抗, Ω ; α — — 钻柱内孔单位长度功率衰减系数, dB/m; α ij, TM, α ij, TE— — TMij、TEij波在波导内的衰减系数, m-1; β n— — 等径波导段的相移常数; Γ L— — 输出端口向负载的反射系数; Γ n— — 反射面的反射系数; Γ N— — N根钻杆级联波导输入反射系数; Γ s— — 输入端口向信号源的反射系数; ε 0— — 真空介电常数, F/m; λ — — 实际波长, m; λ n— — TE11波形在不同内径圆波导中对应的截止波长, m; λ ij, TM, λ ij, TE— — TMij、TEij波在波导内的截止波长, m; μ — — 波导导体内的磁导率, H/m; μ 0— — 真空磁导率, H/m; ρ ij— — 第1类i阶贝塞尔函数的第j个根, 无因次; ${{{\rho }'}_{ij}}$— — 第1类i阶贝塞尔函数导数的第j个根, 无因次; σ — — 波导导体内的电导率, S/m。

The authors have declared that no competing interests exist.

参考文献
[1] 李皋, 李诚, 孟英峰, 等. 气体钻井随钻安全风险识别与监控[J]. 天然气工业, 2015, 35(7): 66-72.
LI Gao, LI Cheng, MENG Yingfeng, et al. While-drilling safety risk identification and monitoring in air drilling[J]. Natural Gas Industry, 2015, 35(7): 66-72. [本文引用:1]
[2] CHEN W Y, FANG B, WANG Y. MWD drilling mud signal de-noising and signal extraction research based on the pulse-code information[C]//Proceedings of the 2010 International Conference on Wavelet Analysis and Pattern Recognition. Qingdao: IEEE, 2010. [本文引用:1]
[3] LI W, NIE Z P. Wireless transmission of MWD and LWD signal based on guidance of metal pipes and relay of transceivers[J]. IEEE Transactions on Geosciences and Remote Sensing, 2016, 54(8): 4855-4866. [本文引用:1]
[4] DAI J, LIU Q H. Efficient computation of electromagnetic waves in anisotropic orthogonal-plano-cylindrically layered media using the improved numerical mode matching method[J]. IEEE Transactions on Antennas & Propagation, 2015, 63(8): 3569-3578. [本文引用:1]
[5] 杜睿攀. 随钻测量数据的井下无线电磁传输系统设计研究[D]. 西安: 西安石油大学, 2013.
DU Ruipan. Design and research on down-hole wireless electromagnetic transmission system of measurement-while-drilling (MWD) data[D]. Xi’an: Xi’an Shiyou University, 2013. [本文引用:2]
[6] 邵春. 基于小波提高EM-MWD接收信号识别精度[D]. 北京: 中国地质大学(北京), 2017.
SHAO Chun. Improve recognition accuracy of EM-MWD received signal based on wavelet[D]. Beijing: China University of Geosciences (Beijing), 2017. [本文引用:1]
[7] HUSSAIN S, HUELVAN Y, ADAMS W. Measurement while drilling, logging while drilling, and rotary steerable systems performance, benefits, and challenges in managed pressure drilling and underbalanced drilling[R]. SPE 169220-MS, 2014. [本文引用:1]
[8] 孟晓峰, 陈一健, 周静, 等. 钻杆中微波传输特性的分析[J]. 北京师范大学学报(自然科学版), 2010, 46(2): 151-155.
MENG Xiaofeng, CHEN Yijian, ZHOU Jing, et al. Analyzing microwave propagation properties in drilling stem[J]. Journal of Beijing Normal University (Natural Science), 2010, 46(2): 151-155. [本文引用:1]
[9] KONG J A. Electromagnetic wave theory[M]. Beijing: Publishing House of Electronics Industry, 2003: 470-476. [本文引用:1]
[10] 王玉龙. 利用微波解除输气管道中天然气水合物堵塞的可行性研究[D]. 西安: 西安石油大学, 2013.
WANG Yulong. Feasibility study of natural gas hydrate in gas pipeline unplugging by using microwave[D]. Xi’an: Xi’an Shiyou University, 2013. [本文引用:1]
[11] 赵克玉, 许福永. 微波原理与技术[M]. 北京: 高等教育出版社, 2006: 80-93, 240-289.
ZHAO Keyu, XU Fuyong. Microwave theory and technology[M]. Beijing: Higher Education Press, 2006: 80-93, 240-289. [本文引用:4]
[12] 李宁平, 鄢扬, 袁学松. 非线性渐变圆波导的数值分析[J]. 真空电子技术, 2009(1): 44-47.
LI Ningping, YAN Yang, YUAN Xuesong. Numerical analysis of nonlinear circular wave guide taper[J]. Vacuum Electronics, 2009(1): 44-47. [本文引用:1]
[13] 陶亚雄. 现代通信原理[M]. 北京: 电子工业出版社, 2013: 8-13.
TAO Yaxiong. Modern communication principle[M]. Beijing: Electronics and Industry Press, 2013: 8-13. [本文引用:1]
[14] 于新华. 高功率毫米波模式变换和传输关键技术的研究[D]. 成都: 电子科技大学, 2010: 14-17.
YU Xinhua. Study of key techniques on high-power millimeter wave mode conversion and transmission[D]. Chengdu: University of Electronic Science and Technology of China, 2010: 14-17. [本文引用:1]
[15] 田昊展, 徐润章, 肖璐瑶, 等. 石油钻杆与套管间空气层中微波传输模式的分析[J]. 北京师范大学学报(自然科学版), 2012, 48(6): 613-616.
TIAN Haozhan, XU Runzhang, XIAO Luyao, et al. Analyzing microwave propagation in air between drilling stem and its cover tube[J]. Journal of Beijing Normal University (Natural Science), 2012, 48(6): 613-616. [本文引用:1]
[16] 李冰玉, 张申. 隧道内微波多径传播特性的仿真[J]. 微波学报, 2003, 19(4): 37-41.
LI Bingyu, ZHANG Shen. The simulation of multipath propagation characteristic of microwave in a tunnel[J]. Journal of Microwaves, 2003, 19(4): 37-41. [本文引用:1]
[17] 巨琰. 无线超宽带信道模型的分析与仿真[D]. 南京: 南京邮电大学, 2013: 42-43.
JU Yan. Modeling and simulation of UWB wireless communication channel[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2013: 42-43. [本文引用:1]
[18] XIA W H, MENG Y F. Study on multipath channels model of microwave propagation in a drill pipe[J]. Journal of Electromagnetic Waves and Applications, 2018, 32(2): 129-137. [本文引用:1]