第一作者简介:谢芳(1987-),女,湖北荆州人,博士,长江大学地球物理与石油资源学院讲师,现主要从事储集层测井评价、成像测井资料处理等方面研究。地址:湖北省武汉市蔡甸区大学路111号,长江大学(武汉校区)地球物理与石油资源学院测井系,邮政编码:430100。E-mail: xiefang1010@qq.com
联系作者简介:刘瑞林(1959-),男,湖北松滋人,博士,长江大学地球物理与石油资源学院教授,现主要从事储集层地球物理评价、成像测井资料处理与解释等方面研究。地址:湖北省武汉市蔡甸区大学路111号,长江大学(武汉校区)地球物理与石油资源学院测井系,邮政编码:430100。E-mail: ruilinabc@263.net
针对碳酸盐岩缝洞储集层中流体流动的非达西渗流特点,应用电成像测井资料图像分割技术,提出一种新的碳酸盐岩缝洞储集层电成像多尺度管流模型产量预测方法。该方法以描述细管中不可压缩流体流动的Hagen-Poiseuille定律为基础,根据碳酸盐岩缝洞储集层井筒内单个缝洞横截面积大小不同这一特征,建立碳酸盐岩缝洞储集层多尺度管流模型,给出碳酸盐岩缝洞储集层多尺度细管平面径向流流量计算公式;引入管流模型产量指数的概念,应用电成像测井资料图像分割结果提取的缝洞面积参数计算管流模型产量指数,最终实现碳酸盐岩缝洞储集层电成像测井资料产量预测。将此方法应用于塔里木盆地北部地区奥陶系碳酸盐岩缝洞储集层,预测结果与实际试油资料吻合较好。
Considering the fluid flow non-darcy characteristics in fracture-vug carbonate reservoirs, a new multi-scale conduit flow model production prediction method for fracture-vug carbonate reservoirs was presented using image segmentation technique of electric imaging logging data. Firstly, based on Hagen-Poiseuille’s law of incompressible fluid flow and the different cross-sectional areas in single fractures and vugs in carbonate reservoirs, a multi-scale conduit flow model for fracture-vug carbonate reservoir was established, and a multi-scale conduit radial fluid flow equation was deduced. Then, conduit flow production index was introduced. The conduit flow production index was calculated using fracture-vug area extracted from the result of electrical image segmentation. Finally, production prediction of fracture-vug carbonate reservoir was realized by using electric imaging logging data. The method has been applied to Ordovician fracture-vug carbonate reservoirs in the Tabei area, and the predicted results are in good agreement with the oil testing data.
塔里木盆地奥陶系碳酸盐岩储集层几乎不发育原生孔隙, 主要靠次生裂缝和溶蚀孔洞提供储渗空间和流体流动通道[1, 2, 3]。对于碳酸盐岩缝洞储集层, 流体的流动主要受孔隙结构和孔隙尺寸的影响。碳酸盐岩孔隙空间复杂, 非均质程度较强的次生孔隙空间(裂缝、溶蚀孔洞)发育[4], 以达西渗流为基础的产量预测模型对碳酸盐岩缝洞储集层精度较低。
国内外研究者应用测井资料进行的产量预测工作可分为两类。第1类以达西渗流理论为基础, 建立相应的地层模型, 推导相应的产量预测公式, 然后利用测井资料计算的参数进行产量预测[5, 6, 7, 8]。这种方法以达西渗流理论为基础, 不适用于碳酸盐岩缝洞储集层, 因为碳酸盐岩缝洞储集层储集空间为缝洞, 流体在缝洞中的流动不是达西渗流。第2类是利用测井资料计算储集层特征参数, 再结合试油资料, 建立经验关系或利用人工智能、模式识别等方法进行产量预测[9, 10, 11, 12, 13, 14, 15]。这种方法对地区经验依赖较大, 由于没有先验的理论作为基础, 需要大量的数据建立模型。
电成像测井是一种测量井壁附近地层电导率图像的测井方法。由于不同地质体电导率不同, 因而电成像测井资料能以图像的形式反映井壁附近地层中的裂缝、溶蚀孔洞、层理等地质现象。在纯的碳酸盐岩缝洞储集层井段, 应用图像分割技术[16, 17]可从电成像测井图像上提取缝洞参数表征缝洞储集层的有效性。目前还尚未见到考虑碳酸盐岩缝洞储集层流体流动特征, 应用电成像测井资料图像分割提取的缝洞参数进行产量预测的报道。
考虑碳酸盐岩缝洞储集层流体在裂缝和连通的溶蚀孔洞中的流动近管流这一特征, 本文以描述细管中不可压缩流体流动的Hagen-Poiseuille定律为基础, 推导碳酸盐岩缝洞储集层多尺度细管平面径向流流量计算公式; 引入管流模型产量指数的概念, 应用电成像测井资料图像分割结果提取的缝洞面积参数计算管流模型产量指数, 建立一种新的适用于碳酸盐岩缝洞储集层的多尺度管流模型产量预测方法, 并应用塔里木盆地北部地区奥陶系碳酸盐岩储集层资料验证本方法的可靠性。
塔里木盆地奥陶系碳酸盐岩缝洞储集层主要储渗空间为溶蚀裂缝和溶蚀孔洞, 地层钻开后井筒及井周地层剖面如图1a所示。流体在溶蚀裂缝和尺度大的溶蚀孔洞中的流动满足黏性不可压缩流体的Navier-Stokes方程[18, 19]。地层中裂缝宽度较大(如裂缝宽度大于2 mm)时, 流体的流动可近似地等效为穿过井筒无限延伸、有限长的平板间的恒定层流问题, 为近似的形状不规则的Hagen-Poiseuille流动[20, 21]。碳酸盐岩地层中溶蚀孔洞的形成一般要经过长时间的溶蚀, 有很长的溶蚀路径。溶蚀孔洞溶蚀路径的长度相对于溶蚀孔洞的孔径(直径小于2 mm的称为孔, 直径大于2 mm的称为洞)要大得多, 因此, 流体在溶蚀孔洞中的流动可以近似地等效为细管中的流体流动问题。在采油状态下, 流体在溶蚀孔、洞中的流速不高, 流动近似层流。不可压缩黏性流体在细管中的层流问题是Hagen- Poiseuille流动[22]。综合考虑, 对于不同孔径的溶蚀孔洞、有限长裂缝中流体流向井筒的流动, 将其统一等效成不同横截面积的细管中流体流向井筒的流动。
描述单个细管中不可压缩牛顿流体流动的Hagen- Poiseuille定律的流量表达式为:
$Q=\frac{\text{ }\!\!\pi\!\!\text{ }\Delta p{{R}
{4}}}{8\eta \Delta L}=\frac{\Delta p{{A}
{2}}}{8\text{ }\!\!\pi\!\!\text{ }\eta \Delta L} (1)$
由(1)式可知, 不可压缩牛顿流体流经细管的流量与细管的压力梯度成正比, 与细管的横截面积的平方成正比, 其微分形式为:
$Q=\frac{{{A}
{2}}}{8\text{ }\!\!\pi\!\!\text{ }\eta }\frac{\text{d}p}{\text{d}L} (2)$
将储集层流体在溶蚀裂缝和连通的溶蚀孔洞中的流动简化为管流, 与颗粒砂岩中流体的流动有重大区别。在后面的推导中, 假定Hagen-Poiseuille定律可以用来描述流体在碳酸盐岩缝洞储集层单个溶蚀裂缝或连通的溶蚀孔洞中的流动, 将溶蚀裂缝和连通的溶蚀孔洞等效成横截面积大小不一的多个细管, 建立碳酸盐岩缝洞储集层多尺度管流模型。
设Ai为井壁处第i个等效细管的横截面积(见图1b), \(\frac{\text{d}{{p}_{i}}}{\text{d}{{L}_{i}}}\)为第i个等效细管压力梯度。对于碳酸盐岩缝洞储集层多尺度管流模型, 储集层中流体流量计算公式的微分形式为:
$Q=\sum\limits_{i}{\frac{A_{i}
{2}}{8\text{ }\!\!\pi\!\!\text{ }\eta }\frac{\text{d}{{p}_{i}}}{\text{d}{{L}_{i}}}} (3)$
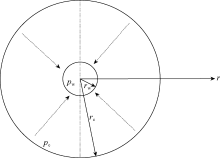
假设实际地层流体从径向深处到井筒的流动为平面径向流动, 压力差仅存在于径向, 垂向没有窜流(见图2)。平面径向流动关于井眼中心对称, 在圆柱坐标系中, 流体管流流量可表示为:
$Q=\sum\limits_{i}{\frac{A_{i}
{2}}{8\text{ }\!\!\pi\!\!\text{ }\eta }\frac{\text{d}{{p}_{i}}}{\text{d}{{r}_{i}}}}=\frac{\sum\limits_{i}{A_{i}
{2}}}{8\text{ }\!\!\pi\!\!\text{ }\eta }\frac{\text{d}p}{\text{d}r} (4)$
将(4)式改写为:
$Q\text{d}r=\frac{\sum\limits_{i}{A_{i}
{2}}}{8\text{ }\!\!\pi\!\!\text{ }\eta }\text{d}p (5)$
对供给半径积分得:
$\int_{{{r}_{\text{w}}}}
{{{r}_{\text{e}}}}{Q\text{d}r}=\frac{\sum\limits_{i}{A_{i}
{2}}}{8\text{ }\!\!\pi\!\!\text{ }\eta }\int_{{{p}_{\text{w}}}}
{{{p}_{\text{e}}}}{\text{d}p} (6)$
即可得到碳酸盐岩缝洞储集层多尺度细管平面径向流流量公式:
$Q\left( {{r}_{\text{e}}}-{{r}_{\text{w}}} \right)=\frac{\sum\limits_{i}{A_{i}
{2}}}{8\text{ }\!\!\pi\!\!\text{ }\eta }\left( {{p}_{\text{e}}}-{{p}_{\text{w}}} \right) (7)$
对(7)式两边同时乘以井筒泄油面积(${{A}_{\text{h}}}=2\text{ }\!\!\pi\!\!\text{ }{{r}_{\text{w}}}h$)的平方, 有:
$Q=\frac{{{A}_{\text{h}}}
{2}\left( {{p}_{\text{e}}}-{{p}_{\text{w}}} \right)}{8\text{ }\!\!\pi\!\!\text{ }\eta \left( {{r}_{\text{e}}}-{{r}_{\text{w}}} \right)}\frac{\sum\limits_{i}{A_{i}
{2}}}{{{A}_{\text{h}}}
{2}} (8)$
上式中\(\frac{\sum\limits_{i}{A_{i}
{2}}}{{{A}_{\text{h}}}
{2}}\)的含义是井壁次生裂缝和连通溶蚀孔洞横截面积平方和与井壁泄油面积平方之比, 它的大小与裂缝-溶蚀孔洞横截面积在井壁所占比例有关, 将此参数定义为管流模型产量指数:
\({{C}_{\text{h}}}=\frac{\sum\limits_{i}{A_{i}
{2}}}{{{A}_{\text{h}}}
{2}}\times 100% \ \ (9)\)
将上式代入(8)式得:
$Q=\frac{{{A}_{\text{h}}}
{2}\left( {{p}_{\text{e}}}-{{p}_{\text{w}}} \right)}{8\text{ }\!\!\pi\!\!\text{ }\eta \left( {{r}_{\text{e}}}-{{r}_{\text{w}}} \right)}{{C}_{\text{h}}} (10)$
由(10)式可见, 碳酸盐岩缝洞储集层产量与供给半径内的压力梯度\(\left( \frac{{{p}_{\text{e}}}-{{p}_{\text{w}}}}{{{r}_{\text{e}}}-{{r}_{\text{w}}}} \right)\)的大小成正比, 与地层流体的黏度成反比, 与井筒的泄油面积的平方成正比, 与管流模型产量指数成正比。当储集层供给半径内压力梯度、地层流体性质及井筒泄油面积一定时, 碳酸盐岩缝洞储集层产量仅取决于管流模型产量指数。
应用电成像图像分割技术能从浅侧向电阻率刻度后的电成像图像上分割出清晰的井壁裂缝-溶蚀孔洞子图像, 提取裂缝、溶蚀孔洞的横截面积等几何参数[16, 17]。电成像测井资料图像分割与缝洞参数提取是计算管流模型产量指数的基础。
应用针对电成像图像设计的一套多目标边缘拾取及目标几何参数提取算法求取电成像裂缝-溶蚀孔洞子图像中单个裂缝-溶蚀孔洞目标的边缘坐标, 计算每一个裂缝-溶蚀孔洞目标的面积。
电成像多目标边缘拾取及目标几何参数提取算法流程如图3所示, 该方法的思路是, 首先求取单个目标的边缘点序列, 统计记录目标边缘点序列内的像素点数, 并抹去目标; 然后移动至下一个目标, 拾取下一个目标的边缘点序列, 统计记录目标边缘点序列内的像素点数; 如此循环往复, 直至拾取完输入图像内的所有目标。
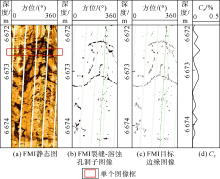
图4为电成像图像分割和多目标拾取试验结果图, 其中图4c是拾取的电成像裂缝-溶蚀孔洞子图像中所有目标的边缘, 拾取出电成像裂缝-溶蚀孔洞子图像中每个目标的边缘之后, 即可统计记录下每个目标边缘内的像素点数。
电成像多目标拾取算法能够拾取记录电成像裂缝-溶蚀孔洞子图像中单个裂缝或溶蚀孔洞目标边缘内的像素点数, 即单个裂缝或溶蚀孔洞目标的面积(Ai)。
应用电成像测井资料在逐点计算管流模型产量指数时, 以一个图像框为基本单元进行计算, 如图4所示。图像框纵向上的长度就是逐点计算管流模型产量指数的采样间隔。电成像测井的极板不能完全覆盖井壁, 单个图像框内的像素点仅覆盖部分井壁。设电成像测井资料的井眼覆盖率为β , 图像框的面积(像素点数)为Fz, 则图像框面积对应的实际井壁面积为\({{A}_{z}}=\frac{{{F}_{z}}}{\beta }\)。在此情况下, (8)式变为:
${{Q}_{z}}=\frac{{{\left( \frac{{{F}_{z}}}{\beta } \right)}
{2}}\left( {{p}_{\text{e}}}-{{p}_{\text{w}}} \right)}{8\text{ }\!\!\pi\!\!\text{ }\eta \left( {{r}_{\text{e}}}-{{r}_{\text{w}}} \right)}\frac{\sum\limits_{i}{A_{i}
{2}}}{{{\left( \frac{{{F}_{z}}}{\beta } \right)}
{2}}}=\frac{{{F}_{z}}
{2}\left( {{p}_{\text{e}}}-{{p}_{\text{w}}} \right)}{8\text{ }\!\!\pi\!\!\text{ }\eta \left( {{r}_{\text{e}}}-{{r}_{\text{w}}} \right)}\frac{\sum\limits_{i}{A_{i}
{2}}}{{{F}_{z}}
{2}} (11)$
对应的成像测井图像框内的管流模型产量指数变为:
${{C}_{z}}=\frac{\sum\limits_{i}{A_{i} {2}}}{{{A}_{z}} {2}}\times 100% $(12)
将(12)式代入(11)式得:
${{Q}_{z}}=\frac{{{F}_{z}}
{2}\left( {{p}_{\text{e}}}-{{p}_{\text{w}}} \right)}{8\text{ }\!\!\pi\!\!\text{ }\eta \left( {{r}_{\text{e}}}-{{r}_{\text{w}}} \right)}{{C}_{z}} (13)$
Qz是一个图像框深度间隔内的流量, 对于每一个图像框计算得到逐点的管流模型产量指数Cz, 由于已考虑了不同仪器井眼覆盖率的影响, Cz对于不同的井含义是相同的。
利用电成像图像分割结果计算管流模型产量指数的具体流程步骤如图5所示:①输入一个图像框的电成像图像分割结果数据; ②对输入图像框内的单个极板的图像分割结果进行多目标边缘拾取处理, 记录每个裂缝或溶蚀孔洞目标的面积; ③移动至下一个极板, 直至处理完所有的极板; ④根据管流模型产量指数定义式计算单个图像框的管流模型产量指数; ⑤移动至下一个图像框, 直至处理完整个井段, 输出管流模型产量指数数据。管流模型产量指数随深度的变化如图4d所示。
将碳酸盐岩缝洞储集层管流模型产量预测方法应用于塔里木盆地北部地区奥陶系碳酸盐岩缝洞储集层, 计算管流模型产量指数, 结合试油产量数据建立该地区奥陶系碳酸盐岩缝洞储集层多尺度管流模型产量预测模型。将得到的产量预测模型应用于实际资料, 对比预测产量与实际试油产量, 验证电成像多尺度管流模型产量预测方法的可靠性。
对塔里木盆地北部地区奥陶系碳酸盐岩电成像测井资料进行图像分割处理, 计算管流模型产量指数, 剔除硅质团块发育段、含泥层段、泥质纹层、缝合线等非储集层段, 统计8口井9个试油层段12个溶蚀孔洞型、裂缝型及裂缝-溶蚀孔洞型储集层的管流模型产量指数, 结合试油产量数据建立塔北地区奥陶系碳酸盐岩缝洞储集层多尺度管流模型产量预测模型。
令$B=\frac{{{F}_{z}}
{2}\left( {{p}_{\text{e}}}-{{p}_{\text{w}}} \right)}{8\text{ }\!\!\pi\!\!\text{ }\eta \left( {{r}_{\text{e}}}-{{r}_{\text{w}}} \right)}$, 则(13)式变为:
\[{{Q}_{z}}=B{{C}_{z}} \ \ (14)\]
在单井的整个储集层段内, 由于流体黏度、径向压力梯度不变, 图像框内的像素点数Fz不变, 系数B为常数。储集层段的总流量Q为对所有储集层厚度求和:
\[Q=\sum\limits_{z}{{{Q}_{z}}}=\sum\limits_{z}{B{{C}_{z}}}(15)\]
储集层的采油强度为:
$\bar{Q}=86\ 400\frac{Q}{H}=86\ 400B\frac{\sum\limits_{z}{{{C}_{z}}}}{H}=k{{\bar{C}}_{z}} (16)$
上式中, \({{\bar{C}}_{z}}=\frac{\sum\limits_{z}{{{C}_{z}}}}{H}\)是储集层段厚度内逐点管流模型产量指数的平均值。
实际上, 对于同一缝洞系统的不同井, 其供给半径内的压力梯度亦为一常数。只要供给半径内的流体性质一致, 则不同井之间的k值也应是一个常数, 这是笔者应用部分实际试油井数据标定k值后进行产量预测的依据。
根据(16)式中采油强度与储集层段内管流模型产量指数平均值之间的关系, 同时为保证不同井不同储集层段试油产量数据的一致性, 把试油折日产油量转换为10 mm油嘴工作制度下的折日产油量, 然后除以有效储集层厚度, 得到采油强度。
储集层段平均管流模型产量指数与10 mm油嘴工作制度下的采油强度关系如图6所示。由图6可见, 10 mm油嘴工作制度下的采油强度与根据电成像测井资料计算的管流模型产量指数有很好的线性正相关性, 与碳酸盐岩缝洞储集层多尺度细管平面径向流流量公式一致。这表明前述假设是成立的, 能够用Hagen- Poiseuille定律来描述流体在碳酸盐岩缝洞储集层裂缝和连通的溶蚀孔洞中的流动, 可以将次生裂缝和连通的溶蚀孔洞等效成横截面积大小不一的多个细管。
根据图6中的数据, 按照(16)式和误差平方和最小准则建立塔北地区奥陶系碳酸盐岩溶蚀孔洞型、
裂缝型及裂缝-溶蚀孔洞型储集层多尺度管流模型产量预测模型:
\[\bar{Q}=27\ 350{{\bar{C}}_{z}} \ \ (17)\]
对塔里木盆地北部地区另外8口井逐点计算管流模型产量指数, 扣除硅质团块发育段、含泥层段、泥质纹层、缝合线等非储集层段, 划分出试油井段内的有效储集层段, 统计有效储集层段的平均管流模型产量指数, 应用前面建立的塔北地区奥陶系碳酸盐岩溶蚀孔洞型、裂缝型及裂缝-溶蚀孔洞型储集层多尺度管流产量预测模型进行产量预测。
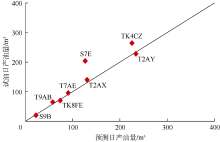
对比表1中的预测日产油量和试油日产量数据可以看出, 除S7E井和TK4CZ井误差较大外, 其余井的预测日产油量和试油日产油量都很接近。预测日产油量和试油日产油量对比关系如图7所示, 可见除S7E井和TK4CZ井数据点以外, 其余数据点均在对角线上或对角线两侧分布, 且分布均匀。表1和图7中的数据说明, 对于塔里木盆地北部地区奥陶系碳酸盐岩地层溶蚀孔洞型、裂缝型及裂缝-溶蚀孔洞型储集层, 电成像多尺度管流模型产量预测方法是可靠的, 其产量预测结果是合理的, 与实际情况吻合。
| 表1 塔北地区奥陶系碳酸盐岩缝洞储集层产量预测结果 |
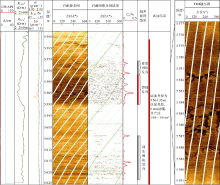
图8为T2AX井管流模型产量指数计算实例, 对该井5 561.35 m以深井段进行试油, 6 mm油嘴工作制度下日产油140~145 m3。综合常规测井资料和成像测井资料及管流模型产量指数曲线划分有效储集层段, 在试油井段内, 5 577.0~5 590.5 m井段为有效储集层段, 5 570.0~5 577.0 m井段和5 605.0~5 624.0 m井段为硅质团块发育段。在塔里木盆地奥陶系硅质团块发育的碳酸盐岩地层少见油气赋存[23], 在产量预测过程中需要扣除这一部分井段。统计的5 577.0~5 590.5 m井段平均管流模型产量指数为0.057%。由(17)式计算该
有效储集层段在6 mm油嘴工作制度下的日产油量为126.895 m3, 与实际酸压试油的日产油量较为接近。
S7E井的预测结果与试油结果差别较大主要是受储集层类型的影响, S7E井5 476.0~5 495.7 m发育溶蚀洞穴, 应用溶蚀孔洞型、裂缝型及裂缝-溶蚀孔洞型储集层多尺度管流模型产量预测模型对其进行产量预测必然会出现较大误差。
碳酸盐岩缝洞储集层电成像多尺度管流模型产量预测方法以电成像测井资料图像分割的裂缝-溶蚀孔洞子图像作为缝洞储集层产量预测依据, 因此, 电成像测井资料图像分割结果的准确性决定了产量预测的准确性。电成像测井资料图像分割的基础是溶蚀缝洞处的导电性与基块岩石的导电性存在差别。在水基钻井液条件下, 由于钻井液的侵入, 溶蚀缝洞处的导电性比岩石基块的导电性好, 这为电成像测井资料图像分割奠定了基础。
塔里木盆地奥陶系碳酸盐岩地层中尚存在一些在电成像测井资料上有类似储集层响应的地质现象, 如泥质纹层、硅质团块、泥质充填裂缝及泥质充填洞穴等, 在电成像测井资料上不易区分, 这些地质现象要结合其他测井资料加以仔细区分, 以排除这些地质现象对电成像图像分割的干扰。
由上面的讨论可以得出碳酸盐岩缝洞储集层电成像测井资料产量预测方法在碳酸盐岩缝洞储集层中的应用条件:①地层为岩性较纯的碳酸盐岩地层, 主要储渗空间为溶蚀缝洞; ②水基钻井液钻井, 井壁附近缝洞处的导电性较基块岩石好; ③储集层段没有泥质纹层、泥质充填缝洞以及硅质团块这些类似储集层的干扰。
对其他岩性的裂缝型地层, 若流体在裂缝中的流动对产量的贡献比流体在岩石基块中的渗流对产量的贡献大得多, 且岩石中没有其他矿物的附加导电性, 如裂缝性火山岩、裂缝性变质岩及裂缝性致密砂岩等, 在有质量较好的电成像测井资料的条件下, 原理上文中的方法也是适用的。
对塔里木盆地奥陶系碳酸盐岩缝洞储集层, 可将不同孔径溶蚀缝洞中流体向井筒的流动等效成横截面积大小不一的细管中流体向井筒的流动。以描述细管中不可压缩流体流动的Hagen-Poiseuille定律为基础, 根据碳酸盐岩缝洞储集层井筒内单个缝、洞横截面积大小不同这一特征, 给出了碳酸盐岩缝洞储集层多尺度细管平面径向流流量计算公式。引入管流模型产量指数的概念, 应用根据电成像测井资料图像分割结果提取的缝洞面积参数计算管流模型产量指数, 实现了碳酸盐岩缝洞储集层电成像测井资料产量预测。应用上述产量预测方法建立塔里木盆地北部地区奥陶系碳酸盐岩缝洞储集层产量预测模型, 预测结果与实际试油资料吻合较好。本文方法有一定使用条件:①地层为岩性较纯的碳酸盐岩地层, 主要储渗空间为溶蚀缝洞; ②水基钻井液钻井, 井壁附近缝洞处的导电性较基块岩石好; ③储集层段没有泥质纹层、泥质充填缝洞以及硅质团块这些类似储集层的干扰。
符号注释:
A— — 细管的横截面积, m2; Ah— — 井筒泄油面积, m2; Ai— — 井壁处第i个等效细管的横截面积, m2; Az— — 图像框面积对应的实际井壁面积, m2; B— — 常数, m3/s; Ch— — 管流模型产量指数, %; Cz— — 成像测井图像框内的管流模型产量指数, %; \({{\bar{C}}_{z}}\)— — 储集层段内管流模型产量指数平均值, %; Fz— — 图像框的面积, m2; h— — 储集层厚度, m; H— — 有效储集层段厚度, m; i— — 等效细管序号; k— — 常数, m3/(d· m); L— — 细管长度, m; Li— — 井壁处第i个等效细管的长度, m; Δ L— — 细管长度的变化量, m; n— — 边缘点数, 无因次; p— — 压力, MPa; pe— — 地层供给边界压力, MPa; pi— — 井壁处第i个等效细管的压力, MPa; pw— — 井底压力, MPa; Q— — 流量, m3/s; Δ p— — 沿细管方向压力的变化量, MPa; Qz— — 1个图像框深度间隔内的流量, m3/s; $\bar{Q}$— — 采油强度, m3/(d· m); r— — 径向距离, m; re— — 地层供给半径, m; ri— — 第i个等效细管到井眼中心的径向距离, m; rw— — 井眼半径, m; R— — 细管的半径, m; β — — 电成像测井资料的井眼覆盖率, %; η — — 流体黏度, 106 Pa· s。下标:z— — 图像框区域序号。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|