第一作者简介:高永海(1977-),男,山东临朐人,博士,中国石油大学(华东)石油工程学院副教授,主要从事井控、多相流动与传热、井筒流动安全与保障等方面的教学和研究工作。地址:山东省青岛市黄岛区长江西路66号,中国石油大学石油工程学院,邮政编码:266580。E-mail: upcgaoyh@126.com
联系作者简介:孙宝江(1963-),男,山东高青人,博士,中国石油大学(华东)石油工程学院教授,主要从事石油工程多相流、油气井工程等方面的教学和研究工作。地址:山东省青岛市黄岛区长江西路66号,中国石油大学石油工程学院,邮政编码:266580。E-mail: sunbj1128@126.com
针对深水油井测试过程中低温环境容易引起结蜡进而影响测试作业正常进行、增加作业成本和风险的问题,基于深水测试管柱温压场和析蜡条件计算模型,提出了测试管柱内结蜡区域预测方法,并对结蜡区域的影响因素进行了分析。研究表明:结蜡区域随着测试产量的增加而逐渐减小;随着地温梯度降低、水深增加及产出流体含水率降低,发生结蜡的区域会增大;随着地层压力的增加,结蜡区域略有增大;初开井阶段,由于温压场的共同作用,测试管柱内结蜡区域很大;循环测试关井后,随着关井时间的增加,结蜡区域逐渐增大。研究成果可为深水油井测试期间的井筒结蜡预防工作提供指导,以保证测试工作顺利进行。
During deep water oil well testing, the low temperature environment is easy to cause wax precipitation, which affects the normal operation of the test and increases operating costs and risks. Therefore, a numerical method for predicting the wax precipitation region in oil strings was proposed based on the temperature and pressure fields of deep water test string and the wax precipitation calculation model. And the factors affecting the wax precipitation region were analyzed. The results show that: the wax precipitation region decreases with the increase of production rate, and increases with the decrease of geothermal gradient, increase of water depth and drop of water-cut of produced fluid, and increases slightly with the increase of formation pressure. Due to the effect of temperature and pressure fields, wax precipitation region is large in test strings at the beginning of well production. Wax precipitation region gradually increases with the increase of shut-in time. These conclusions can guide wax prevention during the testing of deep water oil well, to ensure the success of the test.
油气井测试是油气勘探开发中的关键环节, 可为油气藏评价及开发方式确定提供可靠数据[1, 2]。但在深水油井测试作业中, 特殊的低温环境可能引起井筒严重结蜡。在测试期间, 当原油温度降低至蜡的初始结晶温度时, 蜡晶微粒便开始析出[3]。蜡的析出会增大管内流体黏度, 使压力损失增加[4], 蜡晶析出并沉积于管壁将会减小有效管径、增大沿程摩阻[3, 5, 6], 进而影响测试数据的准确性及测试施工效率。
国内外学者针对含蜡原油输送管道及生产期间井筒中的结蜡区域预测、蜡沉积速率计算开展了大量研究。在预测结蜡区域时, 蜡的热力学模型十分重要, 可以结合原油组分确定给定压力下原油的析蜡温度或给定温度下的析蜡压力[7]。对于蜡的热力学模型, 学者们进行了大量的实验和理论研究并提出了一系列数学模型, 用于计算析蜡条件。蜡的热力学模型大致可分为正规溶液模型[8, 9, 10, 11]、聚合体溶液模型[12, 13, 14, 15]、状态方程
模型[16, 17, 18]和原油组成模型[19, 20, 21]4类。在蜡沉积速率方面, 学者们对单相流情况下蜡沉积速率的研究较为成熟, 但对气液两相流情况下蜡沉积的研究还处于初始阶段且主要针对水平管道[22, 23, 24, 25, 26], 对气液两相流条件下井筒中蜡沉积规律的研究较少。
本文针对深水油井测试工况, 基于温压场计算模型, 结合析蜡条件, 对测试期间井筒内结蜡区域进行预测, 分析产量、地温梯度、水深、地层压力、含水率、开关井作业等因素对结蜡区域的影响规律。
测试管柱中温度、压力的分布是影响结蜡区域的重要因素, 通过对气液两相流基本模型的求解, 可以得到测试管柱中温度、压力等参数的分布。气液两相流基本模型主要有均相流动模型、分相流动模型、漂移流动模型及双流体模型4类[27, 28]。均相流动模型将气液两相混合流体处理为均匀介质, 其特性参数按照气液两相介质的平均值进行计算。分相流动模型初步考虑了各相差异, 将气、液两相分开处理, 认为各相流体都有其独立流速和物性参数。漂移流动模型考虑了气、液相之间的相对运动及空隙率和流速沿截面的分布规律。双流体模型将各相流体看作连续介质, 分别对气、液两相建立连续性方程、动量守恒方程和能量守恒方程, 将各方程通过相界面的作用相互耦合。在这几类模型中, 均相流动模型计算简单、应用方便, 但其未考虑气液两相的差异, 误差较大。分相流动模型中各相的流动特性是孤立的。漂移流动模型不能精确表示各相的运动和空间分布。双流体模型仅需满足气液相在局部范围内均是连续介质的假设, 适用于可当作连续介质研究的任意二元混合物, 且可用于多种流型, 所建立的方程包含的内容全面、求解得出的参数丰富、应用广泛[28]。
本文中温度、压力的计算使用改进的双流体模型, 通过求解3个质量守恒方程(分别关于气相、液滴和壁面处液膜, 见(1)式— (3)式)、2个动量方程(分别关于气相、液滴混合物和液膜, 见(4)式— (5)式)和1个混合物能量方程(见(6)式), 计算多相流各参数值。选取微元体, 以双流体模型为基础, 依据守恒定律列出上述方程[29]:
\[\frac{\partial }{\partial t}\left( {{\beta }_{\text{g}}}{{\rho }_{\text{g}}} \right)=-\frac{1}{A}\frac{\partial }{\partial s}\left( A{{\beta }_{\text{g}}}{{\rho }_{\text{g}}}v{}_{\text{g}} \right)+{{\psi }_{\text{m}}}+{{G}_{\text{g}}} \ \ (1)\]
\[\frac{\partial }{\partial t}\left( {{\beta }_{\text{d}}}{{\rho }_{\text{l}}} \right)=-\frac{1}{A}\frac{\partial }{\partial s}\left( A{{\beta }_{\text{d}}}{{\rho }_{\text{l}}}v{}_{\text{d}} \right)-{{\psi }_{\text{m}}}\frac{{{\beta }_{\text{d}}}}{{{\beta }_{\text{l}}}+{{\beta }_{\text{d}}}}+{{\psi }_{\text{e}}}-{{\psi }_{\text{d}}}+{{G}_{\text{d}}} \ \ (2)\]
\[\frac{\partial }{\partial t}\left( {{\beta }_{\text{l}}}{{\rho }_{\text{l}}} \right)=-\frac{1}{A}\frac{\partial }{\partial s}\left( A{{\beta }_{\text{l}}}{{\rho }_{\text{l}}}v{}_{\text{l}} \right)-{{\psi }_{\text{m}}}\frac{{{\beta }_{\text{l}}}}{{{\beta }_{\text{l}}}+{{\beta }_{\text{d}}}}-{{\psi }_{\text{e}}}+{{\psi }_{\text{d}}}+{{G}_{\text{l}}} \ \ (3)\]
\[\frac{\partial }{\partial t}\left( {{\beta }_{\text{g}}}{{\rho }_{\text{g}}}v{}_{\text{g}}\text{+}{{\beta }_{\text{d}}}{{\rho }_{\text{l}}}v{}_{\text{d}} \right)=-\left( {{\beta }_{\text{g}}}\text{+}{{\beta }_{\text{d}}} \right)\frac{\partial p}{\partial s}-\]\[\frac{1}{A}\frac{\partial }{\partial s}\left( A{{\beta }_{\text{g}}}{{\rho }_{\text{g}}}v_{\text{g}}
{\text{2}}+A{{\beta }_{\text{d}}}{{\rho }_{\text{l}}}v_{\text{d}}
{\text{2}} \right)-\frac{1}{2}{{\lambda }_{\text{g}}}{{\rho }_{\text{g}}}{{v}_{\text{g}}}\left| {{v}_{\text{g}}} \right|\frac{{{S}_{\text{g}}}}{4A}-\]
\[\frac{1}{2}{{\lambda }_{\text{in}}}{{\rho }_{\text{g}}}{{v}_{\text{r}}}\left| {{v}_{\text{r}}} \right|\frac{{{S}_{\text{in}}}}{4A}\text{+}\left( {{\beta }_{\text{g}}}{{\rho }_{\text{g}}}+{{\beta }_{\text{d}}}{{\rho }_{\text{l}}} \right)g\cos \alpha \text{+}\] \[{{\psi }_{\text{m}}}\frac{{{\beta }_{\text{l}}}}{{{\beta }_{\text{l}}}+{{\beta }_{\text{d}}}}{{v}_{\text{a}}}+{{\psi }_{\text{e}}}v{}_{\text{in}}-{{\psi }_{\text{d}}}v{}_{\text{d}} \ \ (4)\]
\[\frac{\partial }{\partial t}\left( {{\beta }_{\text{l}}}{{\rho }_{\text{l}}}v{}_{\text{l}} \right)=-{{\beta }_{\text{l}}}\frac{\partial p}{\partial s}-\frac{1}{A}\frac{\partial }{\partial s}\left( A{{\beta }_{\text{l}}}{{\rho }_{\text{l}}}v_{\text{l}}
{\text{2}} \right)-\frac{1}{2}{{\lambda }_{\text{l}}}{{\rho }_{\text{l}}}{{v}_{\text{l}}}\left| v{}_{\text{l}} \right|\frac{{{S}_{\text{l}}}}{4A}+\]
\[\frac{1}{2}{{\lambda }_{\text{in}}}{{\rho }_{\text{g}}}{{v}_{\text{r}}}\left| {{v}_{\text{r}}} \right|\frac{{{S}_{\text{in}}}}{4A}+{{\beta }_{\text{l}}}{{\rho }_{\text{l}}}g\cos \alpha -{{\psi }_{\text{m}}}\frac{{{\beta }_{\text{l}}}}{{{\beta }_{\text{l}}}+{{\beta }_{\text{d}}}}v{}_{\text{a}}-{{\psi }_{\text{e}}}v{}_{\text{in}}+\] \[{{\psi }_{\text{d}}}{{v}_{\text{d}}}-{{\beta }_{\text{l}}}D\left( {{\rho }_{\text{l}}}-{{\rho }_{\text{g}}} \right)g\frac{\partial {{\beta }_{\text{l}}}}{\partial s}\sin \alpha \ \ (5)\]
\[\frac{\partial }{\partial t}\left[ {{\beta }_{\text{g}}}{{\rho }_{\text{g}}}\left( {{E}_{\text{g}}}+\frac{1}{2}v_{\text{g}}
{\text{2}}+gh \right)+{{\beta }_{\text{l}}}{{\rho }_{\text{l}}}\left( {{E}_{\text{l}}}+\frac{1}{2}v_{\text{l}}
{\text{2}}+gh \right)+ \right.\]\[\left. {{\beta }_{\text{d}}}{{\rho }_{\text{d}}}\left( {{E}_{\text{d}}}+\frac{1}{2}v_{\text{d}}
{\text{2}}+gh \right) \right]=\]\[-\frac{\partial }{\partial s}\left[ {{\beta }_{\text{g}}}{{\rho }_{\text{g}}}{{v}_{\text{g}}}\left( {{H}_{\text{g}}}+\frac{1}{2}v_{\text{g}}
{\text{2}}+gh \right)+ \right.\]
\[{{\beta }_{\text{l}}}{{\rho }_{\text{l}}}{{v}_{\text{l}}}\left( {{H}_{\text{l}}}+\frac{1}{2}v_{\text{l}}
{\text{2}}+gh \right)+\left. {{\beta }_{\text{d}}}{{\rho }_{\text{d}}}{{v}_{\text{d}}}\left( {{H}_{\text{d}}}+\frac{1}{2}v_{\text{d}}
{\text{2}}+gh \right) \right]+{{H}_{\text{s}}}+U \ \ (6)\]
在(1)式— (6)式中, 基本未知变量有7个, 包括p、T、vg、vl、β g、β l和β d, 其他未知变量可以利用这些基本变量表示或求解。压力方程可以表示为:
\[\left( \frac{{{\beta }_{\text{g}}}}{{{\rho }_{\text{g}}}}\frac{\partial {{\rho }_{\text{g}}}}{\partial p}+\frac{1-{{\beta }_{\text{g}}}}{{{\rho }_{\text{l}}}}\frac{\partial {{\rho }_{\text{l}}}}{\partial p} \right)\frac{\partial p}{\partial t}=-\frac{1}{A{{\rho }_{\text{g}}}}\frac{\partial }{\partial s}\left( A{{\beta }_{\text{g}}}{{\rho }_{\text{g}}}v{}_{\text{g}} \right)-\]\[\frac{1}{A{{\rho }_{\text{l}}}}\frac{\partial }{\partial s}\left( A{{\beta }_{\text{l}}}{{\rho }_{\text{l}}}v{}_{\text{l}} \right)-\frac{1}{A{{\rho }_{\text{l}}}}\frac{\partial }{\partial s}\left( A{{\beta }_{\text{d}}}{{\rho }_{\text{l}}}v{}_{\text{d}} \right)+\] \[{{\psi }_{\text{m}}}\left( \frac{1}{{{\rho }_{\text{g}}}}-\frac{1}{{{\rho }_{\text{l}}}} \right)+{{G}_{\text{g}}}\frac{1}{{{\rho }_{\text{g}}}}+{{G}_{\text{l}}}\frac{1}{{{\rho }_{\text{l}}}}+{{G}_{\text{d}}}\frac{1}{{{\rho }_{\text{l}}}} \ \ (7)\]
将(1)式— (7)式进行变形后均可以简化成关于7个基本未知变量的函数, 可统一用如(8)式所示的形式表示:
\[{{a}_{1}}\frac{\partial p}{\partial t}+{{a}_{2}}\frac{\partial T}{\partial t}+{{a}_{3}}\frac{\partial {{v}_{\text{g}}}}{\partial t}+{{a}_{4}}\frac{\partial {{v}_{\text{l}}}}{\partial t}+{{a}_{5}}\frac{\partial {{\beta }_{\text{g}}}}{\partial t}+{{a}_{6}}\frac{\partial {{\beta }_{\text{l}}}}{\partial t}+{{a}_{7}}\frac{\partial {{\beta }_{\text{d}}}}{\partial t}+\]\[{{b}_{1}}\frac{\partial p}{\partial s}\text{+}{{b}_{2}}\frac{\partial T}{\partial s}\text{+}{{b}_{3}}\frac{\partial v{}_{\text{g}}}{\partial s}\text{+}{{b}_{4}}\frac{\partial {{v}_{\text{l}}}}{\partial s}+{{b}_{5}}\frac{\partial {{\beta }_{\text{g}}}}{\partial s}\text{+}{{b}_{6}}\frac{\partial {{\beta }_{\text{l}}}}{\partial s}\text{+}{{b}_{7}}\frac{\partial {{\beta }_{\text{d}}}}{\partial s}\text{=}c \ \ (8)\]
析蜡条件的计算采用Rø nningsen等[30]提出的基于Pedersen模型[16]的扩展模型。
当液相(油)和固相(蜡)达到热力学平衡状态时, 液相和固相中某组分的逸度相等, 即:
${{f}_{\text{li}}}={{f}_{\text{s}}}$ (9)
液相逸度可以表示为:
${{f}_{\text{li}}}={{x}_{\text{li}}}{{\varphi }_{\text{li}}}p$ (10)
固相逸度可以表示为:
${{f}_{\text{s}}}={{x}_{\text{s}}}{{\varphi }_{\text{oli}}}p\exp \left[ -\frac{\Delta {{H}_{\text{f}}}}{RT}\left( 1-\frac{T}{{{T}_{\text{f}}}} \right)+\frac{\Delta V\left( p-{{p}_{\text{ref}}} \right)}{RT} \right]$ (11)
(11)式中Δ Hf和Tf采用Won[8]提出的公式计算。
流动测试期间, 初始条件为测试开始时的温度、压力条件, 测试管柱内的温度为外界环境温度, 压力为地面井口回压与测试液液柱静压之和:
\[\left\{ \begin{align} & {{T}_{j\text{0}}}={{T}_{\text{a}j}} \\ & {{p}_{j0}}={{p}_{\text{o}}}+{{\rho }_{\text{t}}}g{{h}_{j}} \\ \end{align} \right. \ \ (12)\]
关井时, 测试管柱内的初始温度为流动测试稳定时管柱内的温度, 初始压力为测试稳定时地面井口回压与产出液液柱静压之和。
\[\left\{ \begin{align} & {{T}_{j\text{0}}}={{T}_{\text{s}j}} \\ & {{p}_{j0}}={{p}_{\text{so}}}+{{\rho }_{\text{o}}}g{{h}_{j}} \\ \end{align} \right. \ \ (13)\]
流动测试期间边界条件为:在一定产量条件下, 井底流压不变, 井底流体温度等于地层温度。
关井期间边界条件为:井底流体温度与地层温度相等, 井底压力为地层压力。
测试管柱内的温度、压力计算模型是复杂的非线性方程组, 需结合初始条件、边界条件等辅助方程, 通过数值计算方法求解。将(1)式— (7)式都简化为(8)式的形式后, 组成方程组, 在求得各项系数的基础上可以进行求解, 文献[28, 29]给出了具体求解过程。依据有限容积法, 采用交错网格将管柱离散为若干个微元体, 其中流速、质量流量等变量存储在微元体的边界上, 压力、温度、质量等变量存储在微元体的中心, 然后采用欧拉方法利用供体格子差分格式进行数值计算。
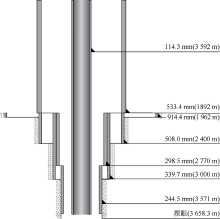
基于温度、压力计算模型及析蜡条件计算模型, 结合安哥拉Louro-2井的数据资料, 对深水油井测试井筒结蜡区域的影响因素进行分析。该深水油井为直井, 基础数据包括:设计井深3 658.3 m, 水深1 892 m, 海水表层温度26 ℃, 海底温度4 ℃, 地温梯度2.92 ℃/100 m, 测试层位地层压力40 MPa、温度55.576 ℃, 产量200 m3/d。油藏流体组分如表1所示, 井身结构如图2所示。在对某一影响因素进行分析时, 只对该影响因素取不同值, 其他参数均使用基础数据。
| 表1 安哥拉Louro-2井油藏流体组分表 |
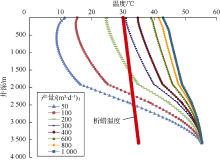
由图3可知, 随着产量的增加, 结蜡区域逐渐减小, 当产量增加到300 m3/d以上时, 整个测试管柱内均不会发生结蜡现象。这是因为在较高产量条件下测试管柱内流体向上流动的流速较快, 与周围环境的热交换少, 温度降幅小。而在该产量范围内由于压力变化导致的析蜡温度曲线变化不大, 故产出流体温度高于析蜡温度的区域很大。产量较低时, 测试管柱内流体与外界低温环境之间换热充分, 导致管柱内流体温度降幅大, 发生结蜡的风险增加。
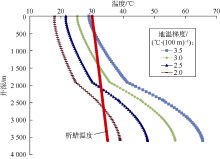
由图4可知, 随着地温梯度的增加, 结蜡区域减小。其原因是当地温梯度较高时测试层位处的温度很高, 从储集层流入井筒的流体温度较高。由于地层段的温度也较高, 在流体从井底向上流动的过程中, 油流热量损失少, 温度降幅小, 整个测试管柱内的温度都较高, 所以结蜡区域较小。
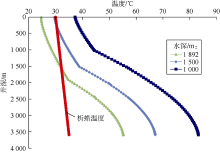
由图5可知, 随着水深的增加, 结蜡区域增大。原因是水深增加后, 海底泥线附近区域的温度较低, 且海水低温段较长, 则油流向上流动的过程中, 向外界散发的热量多, 导致管柱内的温度下降快、降幅大, 容易引起结蜡, 结蜡区域扩大。
由图6可知, 随着地层压力的增加, 结蜡区域增大, 但幅度较小。这是因为, 地层压力增加使测试管柱内的压力也增加。由析蜡条件计算模型可得, 当压力大于流体饱和压力时, 随着压力增加析蜡温度升高。而地层压力变化对管柱内流体温度分布影响很小, 所以结蜡区域略有增大。
由图7可知, 含水率对地层段管柱内温度分布影响不大, 但对海水段管柱内流体温度的影响较为显著。随着含水率的增加, 结蜡区域减小。其原因是水的比热容大于原油的比热容, 高含水率会使流体在向上流动过程中温度降低的幅度减小, 使得整个管柱内流体温度偏高, 结蜡区域减小。
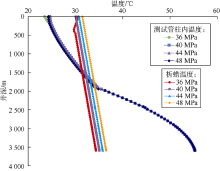
在开井初期, 测试管柱内的压力等于测试液垫静压, 测试管柱内温度较低, 接近外界环境温度(见图8)。
所以在这一阶段, 原油开始在管柱内流动时, 可能发生结蜡的区域很大(见图8)。
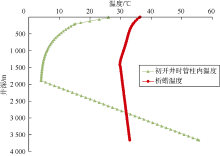
地面关井后, 测试管柱内仍然保持有较高的压力。由图9可知, 在关井初期, 由于管柱内流体与外界环境之间的温差很大, 所以管柱内流体温度降低得很快。随着关井时间的增加, 由于两者温差的减少, 温度降低的幅度也逐渐变小, 管柱内流体温度逐渐降低到接近环境温度。结蜡区域随着关井时间的增加越来越大。所以对这一阶段要给予充分重视, 采取措施降低结蜡风险。
深水油井测试工况下, 在流动测试阶段, 结蜡区域随着产量的增加而逐渐减小, 较低的产量会增加发生结蜡的风险。地温梯度、水深和含水率对结蜡区域有显著的影响, 较低的地温梯度、较大的水深、较低的产出流体含水率会使结蜡区域增大。地层压力对结蜡区域的影响较小, 随着地层压力的增加结蜡区域略有增大。初开井阶段, 由于测试管柱中低温高压环境的存在, 结蜡区域会很大。随着关井时间的增加, 测试管柱内流体温度逐渐降低, 最终降低至接近外界环境温度, 结蜡区域也随着温度的降低而大幅增大。
符号注释:
a1, a2, a3, a4, a5, a6, a7, b1, b2, b3, b4, b5, b6, b7, c— — 系数; A— — 管道截面积, m2; D— — 管径, m; E— — 单位质量内能, J/kg; fli, fs— — 液相、固相逸度, Pa; g— — 重力加速度, 9.8 m/s2; G— — 可能的质量源, 假定是从与管壁成90° 夹角的方向进入, kg/(m3· s); h— — 井深, m; hj— — 微元体j处的垂深, m; H— — 单位质量的焓, J/kg; Hs— — 单位时间单位体积流入的质量源的焓, J/(m3· s); p— — 压力, Pa; pj0— — 微元体j的初始压力, Pa; po— — 地面井口回压, Pa; pref— — 参考状态下压力, Pa; pso— — 测试稳定时地面井口回压, Pa; R— — 通用气体常数, 8.314 J/(mol· K); s— — 长度, m; S— — 湿周, m; t— — 时间, s; T— — 温度, K; Taj— — 微元体j处的地层或海水温度, K; Tf— — 熔解温度, K; Tj0— — 微元体j的初始温度, K; Tsj— — 测试稳定时微元体j处管柱内的温度, K; U— — 单位时间单位体积的传热量, J/(m3· s); v— — 速度, m/s; va— — 相变部分速度, m/s; vr— — 相对速度, m/s; xli, xs— — 液相、固相摩尔分数, %; α — — 管道与垂直方向的夹角, rad; β — — 体积分数, %; Δ Hf— — 正常熔点下的熔解焓, J/mol; Δ V— — 固相和液相摩尔体积差值, m3/mol; φ li— — 液相逸度系数; φ oli— — 标准状态下液相逸度系数; λ — — 摩擦系数; ρ — — 密度, kg/m3; ρ o— — 产出液密度, kg/m3; ρ t— — 测试液密度, kg/m3; ψ d— — 液滴沉积速率, kg/(m3· s); ψ e— — 液滴夹带速率, kg/(m3· s); ψ m— — 相间质量传递速率, kg/(m3· s)。下标:d— — 液滴; g— — 气相; in— — 气、液界面; l— — 壁面处液膜。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|