引用本文
贾虎, 邓力珲. 基于流线聚类人工智能方法的水驱油藏流场识别[J]. 石油勘探与开发, 2018,45(2): 312-319.
JIA Hu, DENG Lihui. Oil reservoir water flooding flowing area identification based on the method of streamline clustering artificial intelligence[J]. Petroleum Exploration & Development, 2018,45(2): 312-319.  
Doi: 10.11698/PED.2018.02.14
Permissions
Copyright©2018, 石油勘探与开发》编辑部
基于流线聚类人工智能方法的水驱油藏流场识别
贾虎, 邓力珲
油气藏地质与开发工程国家重点实验室 西南石油大学,成都 610500

第一作者简介：贾虎（1983-）,男,湖北武汉人,博士,西南石油大学副教授,主要从事油气井化学封堵、提高采收率与油藏工程方面的教学与科研工作。地址：四川省成都市新都区,西南石油大学油气藏地质与开发工程国家重点实验室,邮政编码：610500。E-mail: jiahuswpu@swpu.edu.cn

收稿日期: 2017-08-21
基金项目: 中国石油科技创新基金（2017D-5007-0202）
摘要

以某碳酸盐岩油藏注水开发为例,提出针对流线模拟结果的流场识别方法。在流线模拟计算完成后,利用基于Ocean平台自行编写的插件将流线数据导出,并通过Python编程语言进行后续数据处理及聚类分析,直观反映不同开发阶段水驱油藏流场分布。采用密度峰值聚类算法作为流线聚类主要算法,以轮廓系数算法作为聚类评价算法,选取合理的聚类数,并对不同聚类算法结果进行对比。当聚类数相同时,密度峰值聚类算法比K-means、层次聚类、谱聚类算法对不同类型流线区分能力更强且轮廓系数较高,说明了算法的有效性。依据流线聚类结果可对流场进行量化处理,有效识别油藏中无效注水循环通道以及具有开发潜力的区域,同时可对同一注采井间流线进行细分,描述注采井间水相驱动能力大小分布,为注水优化、井网层系调整、深部调剖等方案决策提供依据。图10表3参23

关键词: 水驱开发; 水驱效率; 流场识别; 流线模拟; 聚类算法; 人工智能
中图分类号:TE344;TE341 文献标志码:A 文章编号:1000-0747(2018)02-0312-08
Oil reservoir water flooding flowing area identification based on the method of streamline clustering artificial intelligence
JIA Hu, DENG Lihui
State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation in Southwest Petroleum University, Chengdu 610500, China
Abstract

For the case of carbonate reservoir water flooding development, the flow field identification method based on streamline modeling result was proposed. The Ocean for Petrel platform was used to build the plug-in that exported the streamline data, and the subsequent data was processed and clustered through Python programming, to display the flow field with different water flooding efficiencies at different time in the reservoir. We used density peak clustering as primary streamline cluster algorithm, and Silhouette algorithm as the cluster validation algorithm to select reasonable cluster number, and the results of different clustering algorithms were compared. The results showed that the density peak clustering algorithm could provide better identified capacity and higher Silhouette coefficient than K-means, hierachical clustering and spectral clustering algorithms when clustering coefficients are the same. Based on the results of streamline clustering method, the reservoir engineers can easily identify the flow area with quantification treatment, the inefficient water injection channels and area with developing potential in reservoirs can be identified. Meanwhile, streamlines between the same injector and productor can be subdivided to describe driving capacity distribution in water phase, providing useful information for the decision making of water flooding optimization, well pattern adjustment and deep profile.

Keyword: water flooding; water flooding efficiency; flow field identification; streamline simulation; cluster algorithm; artificial intelligence
0 引言

中国陆相沉积的碎屑岩和海相沉积的碳酸盐岩油藏, 储集层非均质性较强, 且目前许多高含水砂岩油藏历经长期水驱开发后剩余油分布杂乱且分散, 难以有效认识水驱油藏动用规律, 导致注水开发效率低下。同时地层在经历长时间流体冲刷后易形成优势通道, 导致无效水循环[1], 降低水驱效率。为了更好描述水驱油藏特征, 前人通过水驱特征曲线[2]及井间连通性模型[3]对水驱流场进行了表征。同时, 侯玉培等[1, 4, 5]在流场识别方面做了大量研究, 建立了流场评价体系, 采取层次分析法对流场进行了评价, 但层次分析法需要人为设置评价权重, 因此方案决策存在不确定性。在地质模型基础上, 前人通过流线模拟对生产数据进行拟合并分析了流体运移规律及流动轨迹[6, 7, 8, 9, 10]。与根据孔渗饱分布确定流场强弱的常规方法相比, 流线模拟可更准确且直观地显示出流体主要流通区域。此外, 可依据注水对采油的贡献量对水驱油藏进行注水优化、水驱控制、井网优化[11, 12, 13, 14, 15, 16, 17, 18]。主流的油藏数值模拟软件如Petrel RE虽可准确计算流线分布并依据上述方法进行方案优化, 但缺乏量化分析流场的方法, 且离散的流线分布无法代表实际流场, 也无法区分水相驱动能力不同的流动区域。通过对商业软件Petrel RE进行二次开发实现了流线聚类功能, 可对水相驱动能力不同的流线进行区分并加以分析, 为水驱流场识别提供了一种新的研究手段。

聚类方法又被称为无监督学习, 是人工智能方法的分支之一。不同于通过注采井间配位对流线进行归类的分析方式, 本文采用聚类算法[19]对流线依据其空间位置及流线性质进行聚类, 提取出流场潜在的分布结构。聚类算法以最大化类与类间的差异并最小化类内差异为原则对流线进行聚类, 能确保每一类流线均可最大程度表征其所在的流场, 同时区分出不同类型的流线, 该类无监督学习算法对经验公式与人为评价依赖度较小, 因此对不同类型油藏均具有较好的适用性。

本文以某碳酸盐岩油藏为例, 通过流线聚类方法, 对水相驱动能力不同的流线进行区分并进一步对同一注采井间流线进行细分, 开展流场精细化描述, 找出潜在优势流场, 为水驱流场调整与提高采收率方案决策提供科学依据与技术支撑。

1 流线聚类

流线模拟以流线表示流体长期冲刷而形成的优势通道, 模拟地层流体的流动轨迹。本文通过流线模拟方法表征流场, 以油藏流体在一定时间步长内均沿流线方向流动为基本假设, 流线轨迹通过流线追踪算法[20]获取, 在获取流线轨迹后通过求解沿流线方向的一维质量守恒方程, 即可得到流体沿流线的饱和度分布, 并显示油藏流体流动规律。

流线模拟结果表征了流体性质在离散流线轨迹上的分布, 因此需对流线信息加以提取才可得到流场分布的具体描述。本文通过流线聚类的方法将流场分为不同流动区域, 识别出不同类型流场分布以及该类流场特性, 通过这些信息便可针对性地进行后续油藏开发方案设计。流线聚类步骤包括特征参数提取, 聚类分析及聚类评价。

1.1 特征参数提取

聚类算法需依据样本特征对其进行聚类, 因此需提取出具有区分度且便于实际应用的流线特征, 本文提取的流线特征及公式见表1。其中流线油水体积比由Vow表示, 若该值较大, 则代表沿该流线方向未被注入水波及到的油较多。流线油水流速比由参数vow表示, 该值越大, 则表示沿该流线方向水驱油能力越强。

表1 流线特征及公式

因为流线在z轴方向跨度不大, 故选择流线中点x, y轴坐标表征流线位置。同时, 由于流线模拟计算的数值耗散问题, 部分流线可能出现油水两相流速均接近0的情况, 因此无法通过流体流速直接表征流线位置的水相驱动能力。此外, 对于水驱后期的流场, 水相渗透率往往较高, 而流体饱和度为线性增加的属性, 因此对驱动能力区分效果不明显, 故本文采用油水体积比及油水流速比表征流线位置水相驱动能力, 该方式可对水相饱和度较低而油相饱和度较高的流线进行细分, 同时对水相饱和度大于一定程度的流线进行一定的粗化, 从而最大程度反映不同水相驱动能力的流场分布。

参数选取的意义在于将流线依据其空间位置、驱替效率、波及效率进行聚类, 将具有类似性质的流线归为一类, 从而识别出具有开发价值的油藏区域, 为后期注水优化、井网层系调整、深部调剖等方案决策提供科学依据和技术支撑。

在进行特征提取后, 需对每条流线的特征参数进行归一化处理以便之后的聚类分析。

1.2 聚类分析

聚类分析是一种用于寻找数据之间内在结构的技术。聚类算法有密度峰值、K-means、谱聚类、层次聚类算法等, 其中由于密度峰值聚类算法对数据结构区分能力较强且其结果不具有随机性, 因此本文采用此法。密度峰值聚类算法[19]的基本原理为, 依据与样本性质类似的样本数量的多少作为样本密度, 选取局部区域内密度最大点作为聚类中心, 同时确保其与其他密度更大的样本之间的“ 距离” 相对更大。密度峰值聚类算法流程图见图1。

图1 密度峰值聚类算法流程图

样本i的局部密度计算公式为[19]：

\[{{\rho }_{i}}=\sum\limits_{j}{\chi \left( {{d}_{ij}}\text{}{{d}_{\text{c}}} \right)} \ \ \left( i=1, 2, \cdots , {{n}_{p}} \right) \ \ （1）\]

\[\chi \left( {{d}_{ij}}\text{-}{{d}_{\text{c}}} \right)=\left\{ \begin{align} & 1\ \ \left( {{d}_{ij}}\text{-}{{d}_{\text{c}}}< \text{0} \right) \\ & 0\ \ \left( {{d}_{ij}}\text{-}{{d}_{\text{c}}}\ge \text{0} \right) \\ \end{align} \right.\]

设dc可使样本平均局部密度为总样本数的1%~2%[19], dij通过欧几里得距离公式计算。（1）式计算的结果是离散值, 且易影响算法稳定性, 因此笔者采用指数函数的形式计算局部密度：

\[{{\rho }_{i}}=\sum\limits_{j\ne i}{{{e}
{{{\left( \frac{{{d}_{ij}}}{{{d}_{\text{c}}}} \right)}
{2}}}}} \left( i\text{=}1, 2, \cdots , {{n}_{p}} \right) \ \ （2）\]

同时, 需保证样本与其他比该样本密度更大的样本有较大距离, 设\({{\rho }_{q}}_{_{i}}\)为样本局部密度降序排列的样本序号, 即\({{\rho }_{{{q}_{1}}}}> {{\rho }_{{{q}_{2}}}}> \cdots > {{\rho }_{{{q}_{{{n}_{p}}}}}}\], 则可定义样本分离距离\(h{{\delta }_{{{q}_{i}}}}\)为：

\[{{\delta }_{{{q}_{i}}}}=\left\{ \begin{align} & \underset{{{q}_{j}}, j< i}{\mathop{min}}\, {{d}_{{{q}_{i}}{{q}_{j}}}}\left( i\ge 2 \right) \\ & \underset{j}{\mathop{max}}\, {{d}_{ij}}\left( i\text{=}1 \right) \\ \end{align} \right. \ \ （3）\]

从而得到不同样本的局部密度及分离距离分布（见图2）。

聚类中心应同时具有较大的局部密度与分离距离值, 因此图2内偏离横、纵坐标轴较远处的点可作为聚类中心点, 第i个样本的中心点评价公式为：

\[{{\gamma }_{i}}={{\rho }_{i}}{{\delta }_{{{q}_{i}}}} \ \ （4）\]

图2 样本局部密度与分离距离分布图

若要将总体样本分为nc类, 即可选取依据γ 降序排列在前nc的样本作为聚类中心点。Rodriguez等[21]通过对人工随机生成数据集分析发现, 若以降序排序后的γ 值序号作为横轴, lgγ 值作为纵轴, 则lgγ 曲线从聚类中心过渡到非聚类中心的曲线趋势有明显跳跃, 可为聚类中心选取提供参考, 因此本文取lgγ 值排序曲线趋势出现跳跃的位置作为总样本类数, 即聚类数nc。确定聚类中心后, 将非聚类中心样本与距离最近的聚类中心归为一类。

1.3 聚类评价

聚类数对聚类效果有着极大影响：聚类数过小将粗化数据, 丢失有效信息; 聚类数过大将致使聚类结果无法有效压缩, 造成分析困难。同时, 不同聚类算法如密度峰值、K-means、谱聚类、层次聚类算法等结果往往不尽相同, 因此, 有必要对聚类结果进行评价, 从而选择合理的聚类算法及聚类数。Liu Y等[22]在已知样本真实类别数的情况下, 分析了不同聚类评价算法如Calinski-Harabasz、指数、Dunn、轮廓系数、Davies- Bouldin、Xie-Beni、SD、S-Dbw等是否具有识别出真实样本聚类数的能力。轮廓系数与S-Dbw算法同其他聚类评价算法相比, 对不同的样本类型均能有效识别出样本实际的类别数, 然而S-Dbw算法对离散点较敏感, 结果易出现不连续情况。因此本文采用轮廓系数算法[23], 计算样本的轮廓系数, 根据已评价聚类后的样本与同类样本间平均距离以及样本与非同类样本间平均距离, 对聚类效果进行评价, 轮廓系数值为-1~1, 趋近于1时代表聚类效果相对较优。

2 流场表征

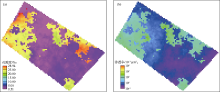
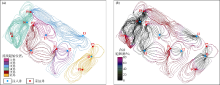
图3为某碳酸盐岩油藏内孔隙度及渗透率分布, 由于溶孔溶洞的存在, 部分区域孔隙度及渗透率较高, 为流体提供了较好的渗流条件。图4为用Petrel RE软件生成的该油藏注水开发6年后通过流线模拟得到的流线分布。图4a为依据流线起点进行分类的结果, 图4b为油相饱和度在流线上的分布。在流线分布图中, 流线越密集则流动强度越大, 由图4流线模拟结果可看出流体流动区域主要集中于渗透率、孔隙度均较高, 即溶孔溶洞较为发育的区域, 如I4井至P4、P6井间区域, 这些区域内渗流条件较好, 因此易形成注入水流动的优势通道。

图3 某碳酸盐岩油藏孔隙度、渗透率分布

图4 通过Petrel RE软件生成的开发6年后流线分类（a）及流线油相饱和度分布（b）

2.1 聚类参数及算法

在获取了流线模拟结果后, 笔者通过自行开发基于Ocean平台的插件实现了与Petrel RE的对接, 能导出表示流线油藏流体、水相流体以及油相流体流动速率的属性数据, 表示流线油相、水相饱和度分布的属性数据以及流线位置数据。

插件将Petrel RE流线数据导出至txt或excel文件, 之后即可通过具有快速开发能力的Python编程语言进行后续数据处理及聚类分析。依据表1公式提取出流线特性后, 进行密度峰值聚类计算, 当设定截断距离为0.01时样本平均局部密度为1.405 3%。由于流线聚类结果对聚类数极为敏感, 不同聚类数下聚类结果有较大差异（见图5）, 因此有必要通过合理的方法选取聚类数。

图5 不同聚类数下流线聚类结果

密度峰值聚类算法通过计算流线样本局部密度与距离属性后依据二者的乘积进行排序, 并选择lgγ 出现跳跃处序号作为聚类数。图6中红色虚线处为跳跃较为明显位置, 表示聚类数为14, 但除该点外, 样本序

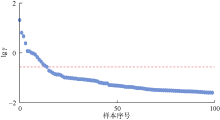
号为4时同样出现非常明显的跳跃, 因此需进一步通过聚类评价算法对聚类结果合理性进行评价。本文采用聚类评价能力较好的轮廓系数聚类评价算法计算不同聚类数下的轮廓系数得分, 并以该得分对水驱开发6年后的流线聚类效果进行评价（见图7）。

图6 不同样本序号下lgγ 分布

图7为依据轮廓系数算法得出的流线聚类结果在不同聚类数下的得分, 得分越接近1代表聚类效果越好。其中红色圆点表示聚类数为14, 可观察到该点处轮廓系数得分最高, 因此合理聚类数为14。以水驱开发6年后油藏流线分布为例, 在取聚类数均为14的情况下, 对比密度峰值聚类算法与K-means、层次聚类、谱聚类算法间的聚类结果。由图8可见, 4种聚类算法计算结果存在差异。

图7 不同聚类数时密度峰值聚类的轮廓系数得分

图8 不同聚类算法结果对比图

密度峰值、K-means、层次聚类、谱聚类4种聚类算法计算结果对应的轮廓系数分别为0.851 914, 0.853 310, 0.850 220, 0.816 990。虽然K-means算法轮廓系数最高, 但K-means算法计算结果具有随机性, 不利于对流场进行确定性分析。其次为密度峰值聚类、层次聚类以及谱聚类。层次聚类算法轮廓系数略低于密度峰值算法, 但该算法受异常点影响较大, 稳定性较差。此外, 谱聚类算法的轮廓系数以及对流线的区分效果较其他算法均较低, 因此本文选择密度峰值聚类算法作为流线聚类的主要算法。

2.2 聚类结果

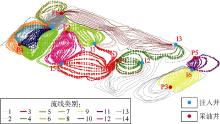
油水流速比与油水体积比可表示流线方向水驱油能力及流线方向未被注入水波及到的油相体积, 因此本文以油水流速比与油水体积比的平均数作为水驱评价系数。该系数越大, 则代表水相驱替效果越好, 按该系数由大至小将流线聚类结果从1到14排序, 结果见图9。与Petrel RE流线模拟结果（见图4）相比, 本文的流线聚类结果对流场进行了有效区分, 有利于找出具有开发潜力的区域, 如I3至P6井间的第2类流线; 还可识别出影响注水效率的无效注水循环区域, 如I4至P6井间的第14类流线以及I6至P5井间的第11类流线; 同时可对属于相同注采井间的流线进行细分, 将其分为具有不同驱动能力的边流与主流：I4至P6井间, 第5类流线为边流, 第14类为主流, I4至P4井间, 第6、第7类为边流, 第10、第13类为主流。这些现象进一步说明流线聚类对不同水相驱动能力流线具有较好区分效果。不同类别流线的流场性质见表2。

图9 开发6年流线聚类图

表2 不同流线类别的流场性质

由表2可见, 不同类流线的油水流速比与油水体积比相差较明显, 说明流线聚类算法对不同类别的流场具有很好的区分能力。同时, 通过该流线聚类分布即可有针对性地分析水相驱动效果较差区域, 如第10至14类流线区域, 这些区域往往位于注采井间连线处（见图9）, 易发生水窜, 影响注水波及系数。因此应选择合理方式调整注水制度, 或是对该区域进行深部调剖, 调整流体流向。此外, 流线聚类方法可依据水驱评价系数识别出注采井间不同类型的流线, 如I4井至P4及P6井区域。该区域因位于溶洞发育区域, 因此流量较大, 流线分布较密集, 第5、第6、第7、第10、第13、第14类流线均位于该区域, 其中水相驱动能力较低的区域为第10、第13、第14类流线, 其水驱评价系数分别为0.155, 0.065, 0.010, 说明该流线区域内主要流通流体为水相, 注采井间形成了优势通道并降低了注入水波及效率, 而该区域内第5、第6、第7类流线水驱效果较好, 水驱评价系数分别为1.150, 0.710, 0.700, 说明在同一注采井间存在水相驱动能力相差较大的流场分布。因此仅对该井进行注水优化无法进一步改善I4井的驱油效果, 可考虑对I4井注入调剖剂, 对具有较大水流量区域进行分流, 增大边流处注水流量以提高波及效率。流线聚类方法同时也可用于寻找油藏内具有开发潜力的区域, 如本次聚类结果中第1、第2、第3类流线, 由于其注采井间无裂缝或溶洞将注采井直接相连, 流体流动相对缓慢, 因此水驱过程相对平缓, 是具有较好开发潜力的区域。

采用密度峰值聚类算法对不同注水开发时刻流线进行聚类的结果见图10。

图10 不同注水开发时刻流线聚类分布

图10反映了流线聚类变化的历史过程, 对应时刻的流场聚类性质见表3。表3中不同类别流线的油水流动比及油水体积比表明, 流线聚类方法对不同时刻的流场均可进行较好的区分, 不同类流线间油水流速比与油水体积比差异较大, 区分效果均较好。

表3 不同注水时间下不同类别流线性质
3 结论

本文为水驱流场识别提供了一种新的研究方法, 以流线聚类的方式将不同类型流场进行区分, 同时依据密度峰值聚类算法及轮廓系数聚类评价算法确定合理聚类数, 确保聚类结果准确性。密度峰值聚类方法结果较稳定, 且对流场区分效果较好, 可作为流线聚类主要算法。

油水流速比及油水体积比可表征流场特征, 依据聚类结果可找出潜在优势流场分布, 有效识别油藏中无效注水循环通道以及具有开发潜力的区域, 在本文流线聚类结果中, 不同类流场间的油水流速比及油水体积比差异较大, 表明区分效果较好; 同时, 流线聚类方法可将同一注采井间的流线细分为主流及支流, 进一步为注水优化、井网层系调整、深部调剖等方案提供科学决策和技术支撑。流线聚类方法在不同注水时刻均可对不同类型流场进行较好的区分, 表明流线聚类算法对流场评价具有较好的适用性。

致谢：感谢斯伦贝谢公司在中国石油工程设计大赛期间为西南石油大学提供的Petrel RE软件及Ocean平台。

符号注释：

a— — 流线; b— — 位于流线上的点; dc— — 截断距离, 无因次; dij— — 样本i, j间的距离, 无因次; 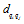— — 样本qi至样本qj的距离, 无因次; i, j— — 样本序号; qi, qj— — 依据局部密度降序排列的第i, j个样本; nc— — 聚类数; na— — 流线a上的总点数; np— — 样本总量; Soab, Swab— — 第a条流线上b点处油相、水相饱和度, %; Vow— — 油水体积比, 无因次; voab, vwab— — 第a条流线上b点处油相、水相流动速率, m3/d; vow— — 油水流速比, 无因次; xab, yab— — 第a条流线上b点处x, y轴坐标; Xa, Ya— — a流线中点位置x, y轴坐标; γ — — 聚类中心评价系数, 无因次; — — 样本的分离距离, 无因次; ρ — — 样本密度, 无因次。

The authors have declared that no competing interests exist.

参考文献
[1] 侯玉培. 整装油藏流场重整提高采收率的数值模拟研究[D]. 东营: 中国石油大学(华东), 2011.
HOU Yupei. Numerical simulation research of uncompartmentalized oilfields by flow field reforming to improve oil recovery[D]. Dongying: China University of Petroleum, 2011. [本文引用:2]
[2] 王继强, 石成方, 纪淑红, 等. 特高含水期新型水驱特征曲线[J]. 石油勘探与开发, 2017, 44(6): 955-960.
WANG Jiqiang, SHI Chengfang, JI Shuhong, et al. New water drive characteristic curves at ultra-high water cut stage[J]. Petroleum Exploration and Development, 2017, 44(6): 955-960. [本文引用:1]
[3] 赵辉, 康志江, 孙海涛, 等. 水驱开发多层油藏井间连通性反演模型[J]. 石油勘探与开发, 2016, 43(1): 99-106.
ZHAO Hui, KANG Zhijiang, SUN Haitao, et al. An interwell connectivity inversion model for waterflooded multilayer reservoirs[J]. Petroleum Exploration and Development, 2016, 43(1): 99-106. [本文引用:1]
[4] 吕琦. 基于流线的油藏数值模拟研究[D]. 东营: 中国石油大学(华东), 2009.
LYU Qi. The research of numerical simulation of reservoir by streamline[D]. Dongying: China University of Petroleum, 2009. [本文引用:1]
[5] 张乔良, 姜瑞忠, 姜平, 等. 油藏流场评价体系的建立及应用[J]. 大庆石油地质与开发, 2014, 33(3): 86-89.
ZHANG Qiaoliang, JIANG Ruizhong, JIANG Ping, et al. Establishment and application of oil reservoir flow-field evaluation system[J]. Petroleum Geology & Oilfield Development in Daqing, 2014, 33(3): 86-89. [本文引用:1]
[6] ANWAR A R, MOHAMED B, MUSTAFA A, et al. An effective streamline history matching technique[R]. SPE 188073, 2017. [本文引用:1]
[7] MILLIKEN W J, EMANUEL A S, CHAKRAVARTY A. Applications of 3D streamline simulation to assist history matching[J]. SPE Reservoir Evaluation & Engineering, 2001, 4(6): 502-508. [本文引用:1]
[8] CHENG H, OYERINDE A S, DATTA-GUPTA A, et al. Compressible streamlines and three-phase history matching[R]. SPE 99465, 2007. [本文引用:1]
[9] SINGH A P, MAUCEC M, KNABE S P. History matching using streamline trajectories[R]. SPE 172146, 2014. [本文引用:1]
[10] BADDOURAH M A, ALTURKI A A, AL-ZAWAWI A S, et al. Streamlines guided assisted history matching methodology: A new approach[R]. SPE 178007, 2015. [本文引用:1]
[11] THIELE M R, BATYCKY R. Water injection optimization using a streamline-based workflow[R]. SPE 84080, 2003. [本文引用:1]
[12] SPYROU C E, ROSA A P L, KHATANIAR S K, et al. An approach to alternative waterflood designs and operations using streamline simulation: Application to an oil field in the North German Basin[R]. SPE 183879, 2017. [本文引用:1]
[13] BUKHAMSEEN N Y, ALNAJEM A A, SAFFAR A H, et al. An injection optimization decision-making tool using streamline based fuzzy logic workflow[R]. SPE 186021, 2017. [本文引用:1]
[14] BATYCKY R P, THIELE M R. Technology update: Mature flood surveillance using streamlines[J]. Journal of Petroleum Technology, 2016, 68(5): 22-25. [本文引用:1]
[15] LI J, LEI Z, LI S, et al. Optimizing water flood performance to improve injector efficiency in fractured low-permeability reservoirs using streamline simulation[R]. SPE 182779, 2016. [本文引用:1]
[16] MØYNER O, KROGSTAD S, LIE K A. The application of flow diagnostics for reservoir management[R]. SPE 171557, 2015. [本文引用:1]
[17] MAQUI A F, ZHAI X, NEGREIRA A S, et al. A comprehensive workflow for near real time waterflood management and production optimization using reduced-physics and data-driven technologies [R]. SPE 185614, 2017. [本文引用:1]
[18] AHONSI W, LAGER A, MUHAIRI L S A, et al. Tracer and streamline modelling for pattern validation and improved reservoir modelling [R]. SPE 181541, 2016. [本文引用:1]
[19] RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496. [本文引用:4]
[20] MATRINGE S F, GERRITSEN M G. On accurate tracing of streamlines[R]. SPE 89920, 2004. [本文引用:1]
[21] RODRIGUEZ A, LAIO A. Supplementary materials for clustering by fast search and find of density[DB/OL]. [2017-12-20]. http://science.sciencemag.org/content/suppl/2014/06/25/344.6191.1492.DC1. [本文引用:1]
[22] LIU Y, LI Z, XIONG H, et al. Understand ing of internal clustering validation measures[R]. Sydney: IEEE, 2010. [本文引用:1]
[23] ROUSSEEUW P. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis[J]. Journal of Computational and Applied Mathematics, 1987, 20(1): 53-65. [本文引用:1]