引用本文
夏鲁, 刘震, 李潍莲, 卢朝进, 杨晓光, 刘明洁. 砂岩压实三元解析减孔模型及其石油地质意义——以鄂尔多斯盆地十里加汗地区二叠系下石盒子组致密砂岩为例[J]. 石油勘探与开发, 2018,45(2): 275-286.
XIA Lu, LIU Zhen, LI Weilian, LU Chaojin, YANG Xiaoguang, LIU Mingjie. Ternary analytic porosity-reduction model of sandstone compaction trend and its significance in petroleum geology: A case study of tight sandstones in Permian Lower Shihezi Formation of Shilijiahan area, Ordos Basin, China[J]. Petroleum Exploration & Development, 2018,45(2): 275-286.  
Doi: 10.11698/PED.2018.02.10
Permissions
Copyright©2018, 石油勘探与开发》编辑部
砂岩压实三元解析减孔模型及其石油地质意义——以鄂尔多斯盆地十里加汗地区二叠系下石盒子组致密砂岩为例
夏鲁1,2, 刘震1,2, 李潍莲1,2, 卢朝进1,2, 杨晓光1,2, 刘明洁3
1. 中国石油大学（北京）油气资源与探测国家重点实验室,北京 102249
2. 中国石油大学（北京）地球科学学院,北京 102249
3. 西南石油大学地球科学与技术学院,成都 610500

第一作者简介：夏鲁（1985-）,男,山东滕州人,现为中国石油大学（北京）地球科学学院在读博士研究生,主要从事致密砂岩油气及岩性油气储集层方面研究。地址：北京市昌平区府学路18号,中国石油大学地质楼825室,邮政编码：102249。E-mail: xialu999@126.com

收稿日期: 2017-08-24
基金项目: 国家自然科学基金（41672124,41502147）; 中国石油“十三五”油气重大专项（2016ZX05047001-002）
摘要

以鄂尔多斯盆地十里加汗地区二叠系下石盒子组致密砂岩为研究对象,定量研究砂岩致密化过程中不同埋深、不同时间、不同压实强度对孔隙度的影响。首先深入分析砂岩压实剖面,其次以黏弹塑性应力-应变模型为基础进行理论推导,然后分别利用多元回归和迭代运算方法来确定砂岩弹性模量和等效黏性系数随埋深和时间的变化趋势,最后建立砂岩压实三元解析减孔模型,并通过与镜下薄片观察结果和常用模型进行对比来证明其合理性。新模型能将减孔量分为弹性减孔、黏塑性减孔和胶结减孔3个部分,针对下石盒子组2段岩屑砂岩的模型计算结果与Houseknecht图版上镜下薄片的统计平均值较为接近,基本上能反映砂岩正常演化趋势上压实与胶结作用的相对强弱。此外,该模型能更合理地解释受溶蚀增孔作用影响不大的砂岩的压实作用,而且能够评价不同埋藏和抬升过程的砂岩压实程度及其对储集层致密化的影响。图12表1参38

关键词: 鄂尔多斯盆地; 二叠系下石盒子组; 压实作用; 胶结作用; 弹性模量; 等效黏性系数; 致密砂岩
中图分类号:TE122.2 文献标志码:A 文章编号:1000-0747(2018)02-0275-12
Ternary analytic porosity-reduction model of sandstone compaction trend and its significance in petroleum geology: A case study of tight sandstones in Permian Lower Shihezi Formation of Shilijiahan area, Ordos Basin, China
XIA Lu1,2, LIU Zhen1,2, LI Weilian1,2, LU Chaojin1,2, YANG Xiaoguang1,2, LIU Mingjie3
1. State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum, Beijing 102249, China
2. College of Geosciences, China University of Petroleum, Beijing 102249, China
3. School of Geoscience and Technology, Southwest Petroleum University, Chengdu 610500, China
Abstract

The tight sandstones in the Permian Lower Shihezi Formation of Shilijiahan area in the Ordos Basin was taken as study object in this research to examine the effects of burial depth, burial time and compaction strength on porosity during densification of reservoir. Firstly, sandstone compaction profiles were analyzed in detail. Secondly, the theoretical study was performed based on visco-elasto-plastic stress-strain model. Thirdly, multiple regression and iterative algorithm were used to ascertain the variation trends of Young’s modulus and equivalent viscosity coefficient with burial depth and burial time, respectively. Accordingly, the ternary analytic porosity-reduction model of sandstone compaction trend was established. Eventually, the reasonability of improved model was tested by comparing with thin-section statistics under microscope and the models in common use. The study shows that the new model can divide the porosity reduction into three parts, namely, elastic porosity loss, visco-plastic porosity loss and porosity loss from cementation. And the results calculated by the new model of litharenite in He 2 Member are close to the average value from the thin-section statistics on Houseknecht chart, which approximately reveals the relative magnitudes of compaction and cementation in the normal evolution trend of sandstone porosity. Furthermore, the model can more exactly depict the compaction trend of sandstone affected little by dissolution than previous compaction models, and evaluate sandstone compaction degree and its contribution to reservoir densification during different burial and uplift processes.

Keyword: Ordos Basin; Permian Lower Shihezi Formation; compaction; Bingham model; Young’s modulus;; equivalent viscosity coefficient; tight sandstone
0 引言

随着油气勘探的快速发展, 致密砂岩气成为新的研究和勘探热点[1]。据新一轮油气资源评价结果, 中国鄂尔多斯、四川等盆地致密砂岩油气资源丰富[2]。对砂岩储集层致密化过程的研究, 有助于明确致密油气储集层的形成过程和深化致密砂岩油气成藏机理。影响砂体孔隙空间大小的因素众多, 如埋深、石英及塑性颗粒含量、粒径大小、分选磨圆程度、早期胶结物的存在与否、沉积背景、构造挤压作用、地层压力异常、埋藏史等[3, 4, 5]。另外, 很多研究表明压实作用与埋藏时间关系密切[6, 7, 8, 9], 地层孔隙度随埋深而减小的过程可以用数学关系式定量表达。早在20世纪30年代, Athy提出的指数关系的数学表达式就被用来定量表示正常压实条件下泥岩孔隙度与埋深之间关系[10], 接着这一模型被用于砂岩压实过程研究。后来又有不少学者提出一些改进的压实模型[11, 12, 13], 但大多数模型还是主要考虑埋藏深度的影响。后来有学者提出了压实作用受埋深和埋藏时间影响的双元函数模型[14], 正在被越来越多的人采纳和关注[15, 16, 17, 18]。目前常用的砂岩压实减孔模型考虑了埋藏深度和时间对砂岩压实的影响, 但并没有深入探讨沉积盆地埋藏过程中砂岩弹性模量和黏性系数的变化, 故难以用数学模型来确定储集层致密化过程中不同埋藏和抬升阶段内压实与胶结作用之间的相对强弱。本文在前人研究基础上, 以鄂尔多斯盆地十里加汗地区二叠系下石盒子组致密砂岩为例, 从压实剖面特征、理论模型推导和地质统计分析的角度深入探讨了砂岩弹性模量和黏性系数随埋藏过程的变化趋势, 并建立了砂岩压实三元解析减孔模型。新模型能更准确地表征埋藏过程（沉降和抬升）对砂岩压实程度的影响, 在一定程度上推动了砂岩储集层致密化过程的定量研究, 提高了致密砂岩储集层评价的准确性。

1 地质概况及研究思路

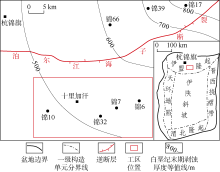
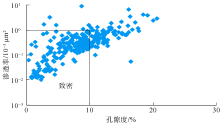
鄂尔多斯盆地十里加汗地区位于泊尔江海子断裂以南（见图1）, 二叠系是该区天然气勘探主要目的层, 可细分为山西组、下石盒子组、上石盒子组、石千峰组。本次研究的目的层是下石盒子组, 自下而上由盒1段、盒2段、盒3段组成, 岩性以岩屑砂岩为主, 为致密砂岩储集层[19]。根据研究区盒1段岩屑砂岩岩心实测孔渗数据可知（见图2）, 多数岩心孔隙度小于10%, 绝大部分砂岩渗透率小于1× 10-3 μ m2。

图1 研究区位置图

图2 盒1段岩屑砂岩岩心实测孔渗交会图

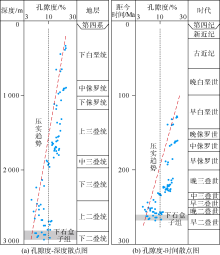
压实剖面上的减孔趋势能够表明砂岩压实作用的强弱[20, 21]。本文先确定现今砂岩孔隙度与埋藏深度、地质年代的关系, 再通过深度域和时间域的压实剖面进行单井和多井压实程度分析。单井砂岩压实剖面特征以锦32井为例（见图3a）, 下石盒子组现今埋深为2 800~2 900 m; 从时间域来看（见图3b）, 下石盒子组沉积期距今260~270 Ma, 压实趋势上相应孔隙度约为3%~5%。多井叠合剖面以锦7、锦10和锦32井3口资料较全的井为例, 将它们的压实剖面叠合到一张图上（见图4a）。时间域内单井压实剖面（见图3b）与多井叠合剖面（见图4a）的趋势和形态基本一致, 即它们的压实趋势都可划分为3段（见图4b、图5a）：上部白垩系砂岩、中部侏罗系和三叠系砂岩及下部二叠系砂岩。

图3 锦32井现今砂岩压实剖面图

前人在分析压实过程中砂岩孔隙度演化时发现：沉积盆地因埋藏过程不同其砂岩压实特征也不一样：先快速埋藏后缓慢沉降（减速型埋藏）的断陷盆地最不利于孔隙保存, 其次是埋藏速率相对均匀（匀速型埋藏）的克拉通盆地, 而先缓慢沉降后快速埋藏（加速型埋藏）的前陆盆地最容易保存原生孔隙[15, 22, 23, 24]。其实, 除不同类型盆地外, 对于相同盆地不同地区或相同地区不同层位, 砂岩压实程度都会因为埋藏过程不同而存在差异。研究表明, 埋藏史曲线与时间轴所围成的面积越大, 压实减孔幅度就越大[15], 十里加汗地区下石盒子组砂岩储集层的埋藏史（见图5b中减速型）属于较为典型的减速型埋藏过程, 往往会导致较强烈的早期压实作用。与匀速型、加速型埋藏过程相比, 该埋藏史曲线与时间轴所围成的面积最大, 一般会表现出较大的压实减孔幅度（见图5b）。

图4 十里加汗地区时间域砂岩压实剖面叠合图

图5 十里加汗地区砂岩压实趋势与埋藏过程对应关系

研究区后期遭受强烈抬升和侵蚀, 压实剖面必须恢复到最大埋深的状态才能显示从浅到深真实的压实趋势[3]。恢复方法是以现今砂岩压实剖面为出发点, 沿着埋藏史逆推直至最大埋深条件（见图5）。以下研究均是基于最大埋深条件下压实剖面展开的。前面时间域压实剖面上3段压实趋势（见图4b）分别对应3种埋藏过程（见图5a）：上段— — 较快埋藏+缓慢抬升; 中段— — 缓慢沉降+较快埋藏+缓慢抬升; 下段— — 快速埋藏+缓慢沉降+较快埋藏+缓慢抬升。鄂尔多斯盆地砂岩孔隙度-深度剖面研究表明：深层压实、胶结作用和浅层压实作用对砂岩减孔趋势的影响具有继承性, 即不同深度段内砂岩压实趋势在半对数坐标系下相互平行或完全一致[16, 17, 25, 26], 十里加汗地区深度域压实剖面也存在类似特征（见图5a）：上段和下段压实趋势基本一致, 一起组成了孔隙度相对较低的趋势（以下简称低孔趋势）; 中段对应着孔隙度相对较高的趋势（以下简称高孔趋势）, 并与低孔趋势基本平行。

时间域内的3段压实趋势对应着深度域内的两类砂岩压实减孔趋势（见图5）：早期的快速埋藏产生了二叠系和白垩系的低孔趋势, 早期的缓慢沉降形成了三叠系和侏罗系的高孔趋势（见图5b）。如果将实际埋藏史等效成匀速埋藏过程, 则低孔和高孔趋势具有不同的平均埋藏速度。以锦32井为例, 低孔趋势的平均埋藏速率约为30 m/Ma, 而高孔趋势的速率约为20 m/Ma（见图5b）。

2 三元解析减孔模型理论分析

在岩石发生弹性变形时, 由于岩石组分之间存在内摩擦, 当上覆负荷增加后不能立即达到最终的变形, 而是随时间延长变形逐渐增加（即蠕变效应）。因此, 砂岩储集层在埋藏过程中既不发生纯弹性变形也不会表现出纯塑性, 而是发生非常复杂的黏弹塑性变形。前人研究表明：黏弹塑性应力-应变模型能够较好地反映多孔介质的受力变形规律, 其中的Bingham模型适合于描述砂岩地层的压实变形特征[14, 15]。针对砂岩压实过程中孔隙度演化, 考虑埋深和地质年代共同影响的双元函数经验模型由此被提出[14, 16, 17, 18]：

\[\phi ={{\phi }_{0}}{{\text{e}}
{az+bzt+ct}} \ \ （1）\]

已有的双元函数模型在推导过程中假设砂岩的弹性模量和黏性系数不随时间变化, 事实上在埋藏压实过程中它们是变化的, 笔者据此对双元函数模型提出改进：对于某一阶段的微小变形而言, Bingham模型应力-应变关系如下[27]：

（2）

研究区虽然靠近断裂构造比较发育的地区, 但并未像盆地西缘冲断带那样经受了强烈的构造挤压作用[28], 因此, 砂岩的上覆地层负荷是造成其压实减孔的最主要原因。当未受到水平方向的构造挤压时, 砂岩在压实过程中的横向应变相对于垂向应变非常小, 可忽略不计。因此可以将压实变形视为垂向压缩的一维情况[15]。当砂岩的变形很微小时, 应变近似等于孔隙度的减

少[9], 即：

\[\varepsilon \approx \Delta \phi \ \ （3）\]

研究区下二叠统砂岩以冲积平原河道相沉积为主, 靠近物源且砂体连通性好[29], 再加上该区北部紧邻长期继承性活动的大断裂— — 泊尔江海子断裂[30], 超压流体很容易排出故难以形成并长期保持异常高压。因此, 砂岩孔隙发生变形的有效应力可以用埋深和密度表示：

\[\sigma ={{10}
{-6}}\left( {{\rho }_{\text{s}}}-{{\rho }_{\text{w}}} \right)gz \ \ （4）\]

与黏塑性变形有关的屈服应力也可表示为：

\[{{\sigma }_{0}}={{10}
{-6}}{{\rho }_{0}}gz \ \ （5）\]

对于已固结砂岩的微小变形阶段, 还需要考虑胶结作用的影响。本文引入反映平均胶结减孔速率快慢的指数, 即平均胶结强度指数（C）。如果将公式（2）中的应力转换成埋藏深度, 则可以改写成如下形式：

\[\frac{\text{d}\Delta \phi }{\text{d}t}=A\frac{1}{E}\frac{\text{d}z}{\text{d}t}+B\frac{z}{\eta }+C \ \ （6）\]

其中 \(A={{10}
{-6}}\left( {{\rho }_{\text{s}}}-{{\rho }_{\text{w}}} \right)g\ \ \ \ B={{10}
{-6}}\left( {{\rho }_{\text{s}}} \right.-{{\rho }_{\text{w}}}-\left. \rho {}_{0} \right)g\)假设砂岩经历一个埋藏速率为k的匀速埋藏过程, 即z=kt, 则上式两边可以同时对时间积分, 由于弹性模量、黏性系数随着埋藏深度和时间变化, 故可以进一步改写为：

\[\phi -{{\phi }_{0}}=A\int_{0}
{z}{\frac{1}{E}\text{d}z}+B\int_{0}
{t}{\frac{z}{\eta }\text{d}t}+Ct \ \ （7）\]

该公式表示在压实趋势上已固结砂岩的减孔模型中包括弹性变形减孔、黏塑性变形减孔和胶结减孔3项, 理论上每一项的系数都应是负值。

3 砂岩弹性模量求取及其变化趋势分析

岩石弹性模量的静态值和动态值不同[31, 32, 33], 静态弹性模量普遍小于动态值, 且两者一般具有较好的线性关系。静态弹性模量是在实验室根据岩心负载情况直接测量其变形强度而得到的, 动态弹性模量是利用岩石的密度和声波速度间接计算的。由于动态弹性模量不能直接应用于地质工程的研究, 而静态值更适合实际地质条件下的负载情况, 故需要建立动、静态参数转换模型[31]。本文以动态弹性模量为桥梁来分析砂岩静态弹性模量随埋深的变化趋势, 先计算动态弹性模量, 再确立动、静态参数转换模型, 最后得到砂岩的静态弹性模量（下文中弹性模量一律指静态弹性模量, 特指动态弹性模量时加上“ 动态” 两字）。依据地层中弹性波的传播理论[32], 岩石动态弹性模量计算公式为：

\[{{E}_{\text{d}}}={{10}
{-6}}\frac{\rho v_{\text{s}}
{2}\left( 3v_{\text{p}}
{2}-4v_{\text{s}}
{2} \right)}{v_{\text{p}}
{2}-v_{\text{s}}
{2}} \ \ （8）\]

岩石密度和速度资料来源于测井数据, 砂岩弹性模量静态值与动态值不同[31, 33], 本文借鉴邻区苏里格气田上古生界砂岩的静态弹性模量与动态弹性模量之间的转换关系[33]：

\[E=0.564{{E}_{\text{d}}}-{{3}_{{}}}494.1 \ \ （9）\]

砂岩弹性模量的变化与其致密化过程密切相关, 低孔砂岩弹性模量往往大于高孔砂岩。砂岩的压实和胶结过程受埋深与埋藏时间双重影响[14, 16]。从十里加汗地区资料比较全的3口井（锦7、锦10和锦32井）中选取砂岩的静态弹性模量、埋深和埋藏时间进行多元回归, 得到低孔趋势下砂岩弹性模量经验公式：

\[{{E}_{\text{l}}}=7.277\ 0\ z-0.025\ 994\ zt+100.18\ t+100 \ \ （10）\]

高孔趋势下砂岩弹性模量经验公式为：

\[{{E}_{\text{h}}}=7.134_{{}}
{{}}3\ z-0.011_{{}}
{{}}351\ zt+36.309\ t+100 \ \ （11）\]

对实际计算的弹性模量和经验公式预测的弹性模量进行线性拟合, 发现它们的相关程度很高（低孔趋势和高孔趋势下线性相关系数分别为0.99和0.81）, 这说明弹性模量的经验公式是可靠的。

4 砂岩等效黏性系数随埋藏变化关系
4.1 砂岩压实阶段孔隙度变化经验公式

砂岩压实过程中的孔隙度变化受埋深与埋藏时间双重影响[14]。对锦7、锦10和锦32井砂岩孔隙度进行多元回归, 得到压实剖面低孔、高孔趋势下孔隙度演化经验公式为：

\[{{\phi }_{\text{l}}}=-0.000\ 151\ z+0.000\ 000\ 711\ zt-0.001\ 33\ t+0.38 \ \ （12）\]

\[{{\phi }_{\text{h}}}=-0.000\ 138\ z+0.000\ 000\ 601\ zt-0.001\ 17\ t+0.40 \ \ （13）\]

根据砂岩压实趋势外推可知该地区低孔趋势下的砂岩在地表处的初始孔隙度约为38%, 高孔趋势下约为40%。

测井解释孔隙度和经验公式计算孔隙度之间相关程度很高（低孔趋势和高孔趋势下线性复相关系数分别为0.99和0.84）, 说明孔隙度经验公式可靠。

4.2 砂岩压实趋势三元解析减孔模型

砂岩弹性模量的经验公式确定之后, 弹性变形减孔项可以描述成一系列微小弹性变形的累加, 即：

\[A\int_{0}
{z}{\frac{1}{E}\text{d}z}=A\sum\limits_{i=0}
{n-1}{\frac{\Delta z}{{{E}_{i}}}}=A\sum\limits_{i=0}
{n-1}{\frac{\Delta z}{m{{z}_{i}}+w{{z}_{i}}{{t}_{i}}+l{{t}_{i}}+{{E}_{0}}}} \ \ （14）\]

如果将实际地层埋藏史等效成一个匀速埋藏过程, 则黏塑性变形减孔项可以变换成如下等效形式：

\[B\int_{0}
{t}{\frac{z}{\eta }\text{d}t}\text{=}{B}'\frac{zt}{{{\eta }_{\text{e}}}}\text{=}{B}'\frac{w}{{{\eta }_{\text{e}}}} \ \ （15）\]

其中 w=zt

故得到如下砂岩压实趋势三元解析减孔模型：

\[\phi =A\sum\limits_{i=0}
{n-1}{\frac{\Delta z}{{{E}_{i}}}}+{B}'\frac{w}{{{\eta }_{\text{e}}}}+Ct+{{\phi }_{0}} \ \ （16）\]

4.3 砂岩压实趋势对比分析和等效黏性系数迭代运算

砂岩等效黏性系数的求取通过砂岩压实剖面上低孔趋势和高孔趋势的对比分析来实现。由于黏塑性变形减孔项未知, 本文采用迭代算法来推算砂岩的等效黏性系数。

4.3.1 三元解析模型的起始系数确定

首先按照一定原则来设计出一个合理的黏塑性变形减孔项, 这个原则是保证模型系数A、B° 和C均为负值, 服从这个原则的函数可以被当作起始模型进行下面的迭代运算。本次研究采用的起始黏塑性变形减孔项如下：

\[{B}'\frac{w}{{{\eta }_{\text{e}}}}={B}'\text{ln}\frac{w}{E} \ \ （17）\]

依据变换后的模型（公式（16））和起始黏塑性变形减孔项（公式（17））, 对前面3口井压实剖面上低孔趋势的数据进行首次多元回归, 得到起始系数如下：A = -12.560 409 885 574 6, B° = -1.308 895 810 302 29, C = -0.111 543 386 958 97。

4.3.2 总减孔量的差值计算

计算差值需要设置一系列从新到旧的时间点并通过两种压实趋势的平均埋藏速率与一系列从浅到深的深度点对应起来。根据砂岩孔隙度的经验关系, 可以计算在每个时间点损失的总孔隙度, 因此, 可以获得同一时间点低孔趋势和高孔趋势的孔隙度损失, 然后将两者相减就能获得同一时间点处两种趋势下砂岩孔隙度损失量的差值。

4.3.3 黏塑性变形减孔量的差值求取

黏塑性变形的孔隙度损失可用总孔隙度损失减去弹性变形孔隙度损失和胶结孔隙度损失来计算。总的孔隙度损失可从经验公式中获得, 弹性变形孔隙度损失可通过三元解析减孔模型的第1项得到, 胶结孔隙度损失能够通过模型的第3项获得。

4.3.4 初次计算得到某一时间点起始等效黏性系数

前面的理论分析表明, 任一阶段的微小变形中的黏塑性变形减孔速率可表示为：

\[\frac{\text{d}\Delta {{\phi }_{2}}}{\text{d}t}\text{=}\frac{\sigma -{{\sigma }_{0}}}{\eta } \ \ （18）\]

根据前面的模型变换过程, 将实际地层埋藏史等效成一个匀速埋藏过程之后, 得到某一埋藏时间处的黏塑性变形减孔量：

\[\Delta {{\phi }_{2}}\text{=}\frac{\sigma -{{\sigma }_{0}}}{{{\eta }_{\text{e}}}}\Delta t \ \ （19）\]

综合考虑高孔趋势和低孔趋势, 它们在同一埋藏时间处的黏塑性变形减孔量的差值与应力、地质年代和等效黏性系数之间存在如下关系：

\[\Delta {{\phi }_{\text{2l}}}-\Delta {{\phi }_{\text{2h}}}=\frac{\left( {{\sigma }_{\text{l}}}-{{\sigma }_{\text{h}}} \right)\Delta t}{{{\eta }_{\text{e}}}} \ \ （20）\]

根据该公式和前面的参数, 可以计算起始等效黏性系数。结果表明, 初次计算得到的等效黏性系数是w的线性函数, 即：

\[{{\eta }_{\text{e0}}}=0.042_{{}}
{{}}586_{{}}
{{}}47w+1_{{}}
{{}}049.930 \ \ （21）\]

用该线性关系模型替换原模型中黏塑性变形减孔项就能得到更为准确的三元解析减孔模型：

\[\phi =A\sum\limits_{i=0}
{n-1}{\frac{\Delta z}{{{E}_{i}}}}+{B}'\frac{w}{pw+q}+Ct+{{\phi }_{0}} \ \ （22）\]

由于首次计算得到的等效黏性系数并不准确, 故还需要进行多次迭代计算。

4.3.5 多次迭代求取等效黏性系数

对首次计算得到的等效黏性系数进行迭代运算, 如果多次迭代之后得到的系数A、B° 和C收敛于固定值, 则可得到最终的等效黏性系数; 如果迭代后的系数无法收敛, 那么通过迭代运算获得等效黏性系数的方法就不可行。根据新模型对原数据进行多元回归得到第1次迭代的系数A、B° 和C; 然后重复前面的步骤直至系数收敛。随着迭代运算次数不断增加, 模型系数逐渐收敛（见表1）, 当迭代运算进行到第6次时, 相关的系数开始收敛于固定的值而不再变化。收敛后的系数分别为：A = -15.278 066 804 189 8, B° = -0.727 700 414 715 871, C = -0.071 757 468 019 331 1。

表1 十里加汗地区砂岩等效黏性系数迭代运算结果

收敛后的等效黏性系数与w之间的关系为：

\[{{\eta }_{\text{e}}}=0.042_{{}}
{{}}297_{{}}
{{}}86\ w+1_{{}}
{{}}041.294 \ \ （23）\]

根据上述方法计算出来的砂岩等效黏性系数从浅到深迅速增大, 数值范围为1 000~10 000 MPa· Ma。前人在研究地壳的长期变形时发现, 在应变速率较慢时, 下地壳岩石黏性系数的数量级从几到数百兆帕百万年[34]。下地壳与浅层砂岩相比具有更高的温度, 其岩石更容易发生黏塑性流动变形, 因而具有相对较小的黏滞系数, 本文结果与前人认识在数量级上大致一致, 这也说明本文的结果是正确的。

5 三元解析减孔模型合理性分析

通过前面的迭代运算已得到了压实剖面上低孔趋势新模型的系数, 该低孔趋势由上部的白垩系减孔段和下部的二叠系减孔段组成（见图5a中的红色趋势线和蓝色趋势线）。石盒子组受溶蚀增孔作用影响不大的岩屑砂岩位于低孔压实趋势上（见图4）, 因此, 该区下石盒子组致密砂岩压实趋势三元解析减孔模型与低孔趋势新模型一致。

5.1 模型计算结果与镜下薄片统计结果比较

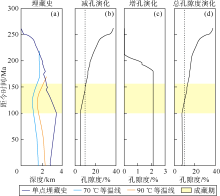
本文模型是一种压实与胶结综合减孔模型, 并未考虑次生增孔效应。利用解析模型能够计算锦32井下石盒子组盒2段岩屑砂岩从开始沉积到最大埋深这一过程的减孔量：总减孔量约为34.6%, 其中最大部分是黏塑性减孔量（即蠕变减孔量）, 约为16.5%（占比为48%）, 弹性减孔量约为8.4%（占比约为24%）, 胶结减孔量为9.7%（占比约为28%）。弹性减孔量和黏塑性减孔量相加即压实减孔量, 则总的压实减孔量约为24.9%, 约占总减孔量的3/4。假设该点砂岩没有发生次生增孔, 则可以模拟综合减孔模型中各类减孔量随地质时期演化的过程（见图6）。假定抬升过程中地温降低, 胶结作用变弱, 对孔隙度影响可以忽略不计, 数值模拟以0.1 m为基本深度间隔, 按照地层实际埋藏和抬升过程进行综合运算, 假定当地层温度大于65 ℃时胶结作用才开始发生[35]。模拟结果表明：弹性减孔和黏塑性减孔速率在早期快速埋藏过程中都很大, 随着深度的增加减孔速率逐渐减小; 在抬升过程中, 弹性变形导致砂岩孔隙度增大而黏塑性变形继续减孔。

图6 埋藏过程中锦32井盒2段砂岩各类减孔量变化

通过镜下薄片观察发现：十里加汗地区下石盒子组岩屑砂岩在沉积成岩过程中经受了强烈的压实作用, 既存在刚性颗粒的紧密接触, 又可见塑性组分的弯曲变形, 总体上表现出较明显的塑性特征（见图7）：①下石盒子组砂岩塑性颗粒含量较多, 最大埋深达3 500 m左右, 强烈的压实导致颗粒之间的接触关系复杂, 既存在颗粒支撑又有杂基支撑; 在塑性颗粒或泥质含量少的局部, 颗粒之间以线接触为主, 点接触与缝合接触的比例均小于20%; 很多地方塑性组分含量多, 在压实过程中易形成泥质充填式杂基、大量假杂基或无胶结物式胶结类型, 刚性颗粒之间表现为点接触, 局部甚至表现为漂浮状的基底式胶结。②有些塑性云母颗粒变形角度大于30° , 甚至可见刚性颗粒破裂。③颗粒出现明显定向排列, 压实定向构造发育, 云母碎片、千枚岩屑等因压实作用强而呈定向分布。

图7 十里加汗地区下石盒子组岩屑砂岩压实作用镜下特征

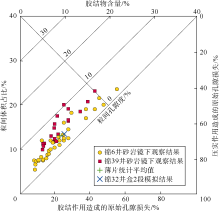
本文采用Houseknecht图版[36]对镜下薄片资料进行定量化研究, 它主要分析压实和胶结作用的影响, 不考虑溶蚀增孔作用。通过铸体薄片统计镜下残余粒间原生孔隙能够得到图版中的粒间孔隙, 利用铸体薄片同时结合普通薄片和阴极发光资料可以统计出胶结物含量, 这两者加起来基本上就等于粒间体积。减孔模型中计算的弹性变形减孔和黏塑性变形减孔都属于压实减孔的范畴, 二者之和便是砂岩压实趋势上的平均压实减孔量, 初始孔隙度减去压实减孔量和胶结减孔量便是砂岩的平均残余粒间孔隙度。模型中的累计胶结减孔量便是平均胶结物含量。计算结果表明, 在整个埋藏成岩致密化过程中压实作用占主导, 三元解析减孔模型计算结果与镜下薄片统计数据平均值较为接近（见图8）, 这说明新模型对减孔效应的解析是合理的。

图8 下石盒子组岩屑砂岩镜下观察统计结果与锦32井盒2段减孔模型计算结果对比

5.2 改进模型与常用模型的对比

以十里加汗地区压实剖面低孔趋势上砂岩数据为例, 对孔隙度和埋深拟合得到Athy指数模型[10]为：

\[\phi =0.38{{\text{e}}
{-0.000_{{}}
{{}}662_{{}}
{{}}3\ z}} \ \ （24）\]

再对孔隙度、埋深和地层年代进行多元回归得到如下双元函数经验模型[16, 17, 18, 26, 37]：

\[\phi =0.38{{\text{e}}
{-\text{0}\text{.000}_{{}}
{{}}\text{391}_{{}}
{{}}\text{507}\ z-0.000_{{}}
{{}}000_{{}}
{{}}\text{844}_{{}}
{{}}\text{487}\ zt-\text{0}\text{.000}_{{}}
{{}}\text{742}_{{}}
{{}}\text{343}\ t}} \ \ （25）\]

5.2.1 砂岩孔隙度散点对比

由砂岩孔隙度散点三维图（见图9）可见, 浅层数据显示双元函数经验模型预测结果与本文的改进模型非常相近, 而Athy模型误差较大; 深层数据表明3种模型的预测结果相关性都很高。因此, 与只考虑埋深的Athy模型相比, 考虑埋深和时间双重影响的三元解析减孔模型更加合理。

图9 3种模型计算孔隙度散点三维对比图

5.2.2 砂岩压实趋势面对比

砂岩压实的孔隙度散点只反映了现今砂岩所经历的特定埋藏过程, 而通过压实模型得到的压实趋势面则几乎代表了所有可能的等效匀速埋藏过程对应的孔隙度演化轨迹。趋势面的对比结果如图10所示, 在时深关系的对角线（即砂岩样品点与初始孔隙度点的连线）附近3种模型的计算结果比较接近且与实测孔隙

度点的相关性较高, 而远离对角线之后压实趋势面的差别开始变大。这种差别在很大程度上证明了双元函数模型明显优于Athy模型（见图10a）, 而三元解析减孔模型（见图10c）比双元函数经验模型（见图10b）更合理, 因为在未埋藏的情况下, 砂岩孔隙度应基本保持不变或发生非常微小的变化。本文新模型的模拟结果与这种认识一致, 而经验模型的趋势面表明即使砂岩一直停留在地表, 其孔隙度在时间效应的作用下也会大幅度减小。

图10 3种压实模型模拟结果的三维趋势面

6 石油地质意义讨论
6.1 低孔渗及致密砂岩储集层致密化机理问题

经典压实减孔Athy模型过分强调了埋藏深度的影响[10], 如何将地质时间和埋藏过程引入压实模型成为一个长期未能解决的问题。本文新模型更合理地引入了地质时间和埋藏过程, 能够更好地评价不同埋藏和抬升过程对砂岩压实程度的影响。模型中的压实减孔可以分为弹性变形减孔和黏塑性变形减孔两部分。砂岩中的刚性组分在压实过程中较多地表现为弹性变形, 其减孔程度与岩石的弹性模量和埋藏深度有关。黏塑性变形往往与砂岩组分（尤其是塑性组分）的转动、滑动、变形、破裂等有关, 能够导致颗粒重新排列和某些结构构造的改变, 这类减孔量不仅与自身的黏性系数和埋藏深度有关, 还受到所经历的地质时间控制, 因此能够反映埋藏和抬升过程的影响。胶结减孔作用受到很多地质因素影响, 尤其是地层温度[22, 23, 24, 35]。通过区分3类不同的减孔作用, 新模型模拟结果比已有的压实模型更加合理（见图9、图10）。

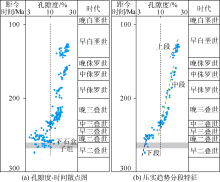
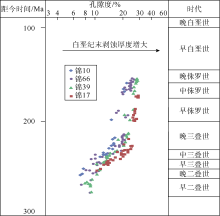
目前不同成岩阶段内压实与胶结作用关系尚不明确, 成藏期后砂岩压实作用对储集层致密化的影响程度尚不清楚。传统方法在评价压实与胶结作用相对强弱时往往采用Houseknecht图版, 该图版考虑的是整个成岩过程[36], 难以评价不同成岩阶段内（尤其是成藏期后）压实与胶结的差异性。本文新模型实现了砂岩减孔过程的定量模拟, 能够评价不同地质时期内压实与胶结作用相互关系（见图6）, 进而推动低孔渗及致密砂岩储集层致密化过程定量研究。此外, 由于新模型区分了弹性变形和黏塑性变形, 因而能够合理地评价抬升过程中的压实作用（见图6）：在地层抬升过程中弹性变形增孔量略大于黏塑性变形减孔量, 进而造成砂岩孔隙度轻微增加。这与研究区附近的地质现象是吻合的：根据前人对杭锦旗地区上白垩统剥蚀厚度恢复结果[38], 锦10、锦66、锦39和锦17井的剥蚀厚度依次增大（见图1）, 砂岩压实剖面上相同地质年代的孔隙度也表现出增大趋势（见图11）。

图11 砂岩孔隙度随埋藏时间的变化趋势

6.2 砂岩储集层物性演化过程定量恢复

基于镜下薄片鉴定资料的古孔隙度恢复方法往往把压实作用的减孔量归结到埋深较浅的早成岩阶段, 而传统数值模拟方法虽然能够考虑整个演化过程中的压实与胶结减孔效应, 但对不同埋藏过程中压实减孔程度的预测不够准确。本文模型实际上是一种减孔效应模型, 它与增孔效应模型相结合就能实现砂岩总孔隙度演化过程模拟。这样的总孔隙度演化模型能够预测不同埋藏和抬升过程中的压实减孔幅度, 并能区分出3类不同的减孔量, 进而发展了已有的砂岩古孔隙度恢复效应模拟方法。利用文献[16]的增孔模型和本文的减孔模型, 结合前人成藏期次的研究[28], 能够得到主成藏期前后锦32井盒2段岩屑砂岩（现今孔隙度为7.7%）孔隙度演化过程（见图12）。

图12 锦32井盒2段岩屑砂岩孔隙度演化过程图（地温70~90 ℃为酸化增孔阶段）

7 结论

三元解析减孔模型理论推导表明, 已固结砂岩减孔模型包括弹性变形减孔、黏塑性变形减孔和胶结减孔3项。在十里加汗地区砂岩压实趋势上, 砂岩弹性模量经验公式能表示成埋深和时间的函数, 砂岩等效黏性系数则是时间深度指数的线性函数。

十里加汗地区下石盒子组岩屑砂岩经受了强烈的压实作用, 造成原生粒间孔隙急剧减小。Houseknecht图版分析表明：①在砂岩的致密化过程中压实作用占主导而胶结作用次之; ②三元解析减孔模型的模拟结果与镜下薄片观察统计数据的平均值较为接近, 基本上能反映砂岩正常演化趋势上压实与胶结的相对强弱。

新的压实模型具有重要的石油地质意义：更合理地引入了地质时间和埋藏过程因素, 能够更好地评价不同埋藏过程对砂岩压实程度的影响; 实现了压实与胶结综合减孔过程的定量模拟, 能够评价不同埋藏阶段内的砂岩压实强度及其对储集层致密化的影响; 作为一种更合理的减孔效应模型, 与增孔效应模型相结合就能定量恢复砂岩总孔隙度演化过程。

符号注释：

a, b, c— — 双元函数拟合常数; A, B— — 弹性和黏塑性减孔项系数, MPa/m; B° — — 等效变换后的黏塑性变形减孔项系数, MPa/m; C— — 平均胶结强度指数, Ma-1; E, Ed— — 静态、动态弹性模量, MPa; E0, El, Eh— — 静态弹性模量初始值、低孔趋势和高孔趋势上砂岩静态弹性模量, MPa; g— — 重力加速度, 本文取9.8 m/s2; i— — 弹性变形单元序号, 无因次; k— — 砂岩埋藏速率, m/Ma; l, m, w— — 砂岩弹性模量经验公式拟合常数; n— — 弹性变形单元总数, 无因次; p, q— — 等效黏性系数与w的线性函数的斜率与截距; t— — 地层经历的埋藏时间, Ma; ∆ t— — 时间增量, Ma; vp, vs— — 岩石纵波和横波速度, m/s; w— — 时间深度指数, 即埋藏时间和埋藏深度的乘积, Ma· m; z— — 地层埋藏深度, m; ∆ z— — 深度增量, m; ε — — 岩石的应变, 无因次; η , η e, η e0— — 黏性系数、等效黏性系数、某一时间点起始等效黏性系数, MPa· Ma; ρ — — 岩石密度, kg/m3; ρ 0— — 与屈服应力相对应的等效密度, kg/m3; ρ s, ρ w— — 上覆地层的平均密度和地层水的平均密度, kg/m3; σ , σ 0— — 岩石受到的有效应力和岩石的屈服应力, MPa; σ 1, σ h— — 低孔趋势和高孔趋势上砂岩受到的有效应力, MPa; ϕ — — 砂岩孔隙度, %; ϕ 0— — 砂岩初始孔隙度, %; ϕ l, ϕ h— — 低孔趋势和高孔趋势上砂岩孔隙度, %; ∆ ϕ — — 砂岩减孔量, %; ∆ ϕ 2— — 某一埋藏时间处的黏塑性变形减孔量, %; Δ ϕ 2l, Δ ϕ 2h— — 低孔趋势和高孔趋势上黏塑性变形造成的孔隙度损失量, %。

The authors have declared that no competing interests exist.

参考文献
[1] 贾承造. 论非常规油气对经典石油天然气地质学理论的突破及意义[J]. 石油勘探与开发, 2017, 44(1): 1-11.
JIA Chengzao. Breakthrough and significance of unconventional oil and gas to classical petroleum geological theory[J]. Petroleum Exploration and Development, 2017, 44(1): 1-11. [本文引用:1]
[2] 贾承造, 郑民, 张永峰. 中国非常规油气资源与勘探开发前景[J]. 石油勘探与开发, 2012, 39(2): 129-136.
JIA Chengzao, ZHENG Min, ZHANG Yongfeng. Unconventional hydrocarbon resources in China and the prospect of exploration and development[J]. Petroleum Exploration and Development, 2012, 39(2): 129-136. [本文引用:1]
[3] SCHERER M. Parameters influencing porosity in sand stones: A model for sand stone porosity prediction[J]. AAPG Bulletin, 1987, 71(5): 485-491. [本文引用:2]
[4] GILES M R, INDRELID S L, JAMES D M D. Compaction: The great unknown in basin modelling[J]. Geological Society London Special Publications, 1998, 141(1): 15-43. [本文引用:1]
[5] 孟元林, 张磊, 曲国辉, 等. 异常低压背景下储集层成岩特征: 以渤海湾盆地辽河坳陷西部凹陷南段古近系为例[J]. 石油勘探与开发, 2016, 43(4): 669-674.
MENG Yuanlin, ZHANG Lei, QU Guohui, et al. Diagenetic characteristics under abnormally low pressure: A case from the Paleocene of southern Western Sag of Liaohe Depression, Bohai Bay Basin[J]. Petroleum Exploration and Development, 2016, 43(4): 669-674. [本文引用:1]
[6] RAYMOND S. Burial history and diagenetic reaction kinetics[J]. AAPG Bulletin, 1983, 67(4): 684-691. [本文引用:1]
[7] SCHMOKER J W, GAUTIER D L. Sand stone porosity as function of thermal maturity[J]. Geology, 1988, 16(11): 1007-1010. [本文引用:1]
[8] BLOCH S. Empirical prediction of porosity and permeability in sand stones[J]. AAPG Bulletin, 1991, 75(7): 1145-1160. [本文引用:1]
[9] 刘震, 武耀辉. 泥岩压实程度与热成熟度关系分析[J]. 地质论评, 1997, 43(3): 290-296.
LIU Zhen, WU Yaohui. Analysis on relation between compaction of mudstone and thermal maturity[J]. Geological Review, 1997, 43(3): 290-296. [本文引用:2]
[10] ATHY L F. Density, porosity and compaction of sedimentary rock[J]. AAPG Bulletin, 1930, 14(1): 1-24. [本文引用:3]
[11] SMITH J E. The dynamics of shale compaction and evolution of pore-fluid pressures[J]. Journal of the International Association for Mathematical Geology, 1971, 3(3): 239-263. [本文引用:1]
[12] BURYAKOVSKIY L A, DJEVANSHIR R D, CHILINGARIAN G V. Mathematical simulation of sediment compaction[J]. Journal of Petroleum Science & Engineering, 1991, 5(2): 151-161. [本文引用:1]
[13] SOMBRA C L, CHANG H K. Burial history and porosity evolution of Brazilian upper Jurassic to Tertiary sand stone reservoirs[C]//KUPECZ J A, GLUYAS J G. Reservoir quality prediction in sand stones and carbonates. Tulsa: AAPG, 1997: 79-89. [本文引用:1]
[14] 刘震, 邵新军, 金博, 等. 压实过程中埋深和时间对碎屑岩孔隙度演化的共同影响[J]. 现代地质, 2007, 21(1): 125-132.
LIU Zhen, SHAO Xinjun, JIN Bo, et al. Co-effect of depth and burial time on the evolution of porosity for classic rocks during the stage of compaction[J]. Geoscience, 2007, 21(1): 125-132. [本文引用:5]
[15] 何小胡, 刘震, 梁全胜, 等. 沉积地层埋藏过程对泥岩压实作用的影响[J]. 地学前缘, 2010, 17(4): 167-173.
HE Xiaohu, LIU Zhen, LIANG Quansheng, et al. The influence of burial history on mudstone compaction[J]. Earth Science Frontiers, 2010, 17(4): 167-173. [本文引用:5]
[16] 潘高峰, 刘震, 赵舒, 等. 砂岩孔隙度演化定量模拟方法: 以鄂尔多斯盆地镇泾地区延长组为例[J]. 石油学报, 2011, 32(2): 249-256.
PAN Gaofeng, LIU Zhen, ZHAO Shu, et al. Quantitative simulation of sand stone porosity evolution: A case from Yanchang formation of Zhenjing area, Ordos Basin[J]. Acta Petrolei Sinica, 2011, 32(2): 249-256. [本文引用:6]
[17] 郭彦如, 刘俊榜, 杨华, 等. 鄂尔多斯盆地延长组低渗透致密岩性油藏成藏机理[J]. 石油勘探与开发, 2012, 39(4): 417-425.
GUO Yanru, LIU Junbang, YANG Hua, et al. Hydrocarbon accumulation mechanism of low permeable tight lithologic oil reservoirs in the Yanchang Formation, Ordos Basin, China[J]. Petroleum Exploration and Development, 2012, 39(4): 417-425. [本文引用:4]
[18] 姚泾利, 唐俊, 庞国印, 等. 鄂尔多斯盆地白豹—华池地区长8段孔隙度演化定量模拟[J]. 天然气地球科学, 2013, 24(1): 38-46.
YAO Jingli, TANG Jun, PANG Guoyin, et al. Quantitative simulation on porosity-evolution in member 8 of Yanchang formation of Baibao-Huachi area, Ordos Basin[J]. Natural Gas Geoscience, 2013, 24(1): 38-46. [本文引用:3]
[19] 谢润成, 周文, 李良, 等. 鄂尔多斯盆地北部杭锦旗地区上古生界砂岩储层特征[J]. 新疆地质, 2010, 28(1): 86-90.
XIE Runcheng, ZHOU Wen, LI Liang, et al. Characteristics of upper Paleozoic sand stone reservoir in Hangjinqi area of Ordos Basin[J]. Xinjiang Geology, 2010, 28(1): 86-90. [本文引用:1]
[20] SELLEY R C. Porosity gradients in North Sea oil-bearing sand stones[J]. Journal of the Geological Society, 1978, 135(1): 119-132. [本文引用:1]
[21] RAMM M. Porosity-depth trends in reservoir sand stones: Theoretical models related to Jurassic sand stones offshore Norway[J]. Marine & Petroleum Geology, 1992, 9(5): 553-567. [本文引用:1]
[22] 朱国华. 成岩作用与砂层(岩)孔隙的变化[J]. 石油与天然气地质, 1982, 3(3): 195-203.
ZHU Guohua. Diagenesis in relation to evolution of pores in sand stone[J]. Oil & Gas Geology, 1982, 3(3): 195-203. [本文引用:2]
[23] 寿建峰, 朱国华. 砂岩储层孔隙保存的定量预测研究[J]. 地质科学, 1998, 33(2): 244-250.
SHOU Jianfeng, ZHU Guohua. Study on quantitative prediction of porosity preservation in sand stone reservoir[J]. Chinese Journal of Geology, 1998, 33(2): 244-250. [本文引用:2]
[24] 罗静兰, 张成立, 阎世可, 等. 盆地埋藏史及其对砂岩储层物性演化的影响: 以陕北延长油区砂岩储层为例[J]. 石油与天然气地质, 2001, 22(2): 123-136.
LUO Jinglan, ZHANG Chengli, YAN Shike, et al. Effect of burial history on physical property of sand stone reservoirs: Take Yanchang oil region in north Shaanxi as an example[J]. Oil & Gas Geology, 2001, 22(2): 123-136. [本文引用:2]
[25] 刘明洁, 刘震, 刘静静, 等. 鄂尔多斯盆地上三叠统延长组机械压实作用与砂岩致密过程及对致密化影响程度[J]. 地质论评, 2014, 60(3): 655-665.
LIU Mingjie, LIU Zhen, LIU Jingjing, et al. The relationship between the mechanical compaction and the densification process of sand stones and the affect degree of compaction to the densifying of Yanchang Formation, Ordos Basin[J]. Geological Review, 2014, 60(3): 655-665. [本文引用:1]
[26] 刘明洁, 刘震, 刘静静, 等. 砂岩储集层致密与成藏耦合关系: 以鄂尔多斯盆地西峰—安塞地区延长组为例[J]. 石油勘探与开发, 2014, 41(2): 168-175.
LIU Mingjie, LIU Zhen, LIU Jingjing, et al. Coupling relationship between sand stone reservoir densification and hydrocarbon accumulation: A case from the Yanchang Formation of the Xifeng and Ansai areas, Ordos Basin[J]. Petroleum Exploration and Development, 2014, 41(2): 168-175. [本文引用:2]
[27] 张清. 岩石力学基础[M]. 北京: 中国铁道出版社, 1986: 135-136.
ZHANG Qing. Rock mechanics foundation[M]. Beijing: China Railway Press, 1986: 135-136. [本文引用:1]
[28] 杨华, 席胜利, 魏新善, 等. 鄂尔多斯盆地大面积致密砂岩气成藏理论[M]. 北京: 科学出版社, 2016.
YANG Hua, XI Shengli, WEI Xinshan, et al. Accumulation theories of large-area tight sand stone gas in Ordos Basin[M]. Beijing: Science Press, 2016. [本文引用:2]
[29] 李婕, 赵俊兴, 孔祥超, 等. 鄂北杭锦旗地区下石盒子组沉积相演化及控制因素[J]. 山东科技大学学报(自然科学版), 2013, 32(2): 34-42.
LI Jie, ZHAO Junxing, KONG Xiangchao, et al. Sedimentary facies evolution and controlling factors of Lower Shihezi Formation in Hangjinqi Area, North Ordos Basin[J]. Journal of Shand ong University of Science and Technology (Natural Science Edition), 2013, 32(2): 34-42. [本文引用:1]
[30] 李潍莲, 纪文明, 刘震, 等. 鄂尔多斯盆地北部泊尔江海子断裂对上古生界天然气成藏的控制[J]. 现代地质, 2015, 29(3): 584-590.
LI Weilian, JI Wenming, LIU Zhen, et al. Control of Boerjianghaizi Fault on gas accumulation of Upper Paleozoic in Northern Ordos Basin[J]. Geoscience, 2015, 29(3): 584-590. [本文引用:1]
[31] 陈勉, 金衍, 张广清. 石油工程岩石力学[M]. 北京: 科学出版社, 2008: 303-304.
CHEN Mian, JIN Yan, ZHANG Guangqing. Petroleum engineering rock mechanics[M]. Beijing: Science Press, 2008: 303-304. [本文引用:3]
[32] 杨秀娟, 张敏, 闫相祯. 基于声波测井信息的岩石弹性力学参数研究[J]. 石油地质与工程, 2008, 22(4): 39-42.
YANG Xiujuan, ZHANG Min, YAN Xiangzhen. Study on acoustic logging-based rock elasticity parameters[J]. Petroleum Geology and Engineering, 2008, 22(4): 39-42. [本文引用:2]
[33] 边会媛, 王飞, 张永浩, 等. 储层条件下致密砂岩动静态弹性力学参数实验研究[J]. 岩石力学与工程学报, 2015, 34(S1): 3045-3054.
BIAN Huiyuan, WANG Fei, ZHANG Yonghao, et al. Experimental study of dynamic and static elastic parameters of tight sand stones under reservoir conditions[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(S1): 3045-3054. [本文引用:3]
[34] 张晁军, 曹建玲, 石耀霖. 从震后形变探讨青藏高原下地壳黏滞系数[J]. 中国科学: 地球科学, 2008, 38(10): 1250-1257.
ZHANG Chaojun, CAO Jianling, SHI Yaolin. Study on viscosity coefficient of lower crust under Tibetan Plateau from post-earthquake deformation[J]. SCIENCE CHINA Earth Sciences, 2009, 52(3): 411-419. [本文引用:1]
[35] 应凤祥, 罗平, 何东博, 等. 中国含油气盆地碎屑岩储集层成岩作用与成岩数值模拟[M]. 北京: 石油工业出版社, 2004: 91-97.
YING Fengxiang, LUO Ping, HE Dongbo, et al. Diagenesis and diagenetic numerical simulation of clastic reservoirs in petroliferous basins of China[M]. Beijing: Petroleum Industry Press, 2004: 91-97. [本文引用:2]
[36] HOUSEKNECHT D W. Assessing the relative importance of compaction processes and cementation to reduction of porosity in sand stones[J]. AAPG Bulletin, 1987, 71(6): 633-642. [本文引用:2]
[37] CAI C E, LIU Z, QIU N S, et al. Hydrocarbon accumulation in the northwest Chaluhe Fault Depression, Yitong Basin, North China[J]. Australian Journal of Earth Sciences, 2015, 62(4): 513-527. [本文引用:1]
[38] 王飞龙. 鄂尔多斯盆地杭锦旗地区上古生界古水动力体系与油气运移成藏[D]. 西安: 西北大学, 2007: 21-28.
WANG Feilong. Study on the palaeohydrodynamic system and hydrocarbon migration and accumulation of Upper Paleozoic in the region of Hangjinqi in Ordos Basin[D]. Xi’an: Northwest University, 2007: 21-28. [本文引用:1]